第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 计算 $x^{2}\cdot 4x^{3}$ 的结果是(
A.$x^{5}$
B.$5x^{5}$
C.$4x^{6}$
D.$4x^{5}$
D
)A.$x^{5}$
B.$5x^{5}$
C.$4x^{6}$
D.$4x^{5}$
答案:
D
2. 若 $2^{a}= 5$,$2^{b}= 3$,则 $2^{a + b}= $(
A.$8$
B.$2$
C.$15$
D.$1$
C
)A.$8$
B.$2$
C.$15$
D.$1$
答案:
C
3. 下列计算正确的是(
A.$-2a^{2}(a^{2}-a + 1)= -2a^{4}+2a^{3}$
B.$(12a^{6}-4a^{3})÷4a^{3}= 3a^{3}$
C.$(a + b)^{2}= a^{2}+b^{2}$
D.$(2a + b)(a + 2b)= 2a^{2}+5ab + 2b^{2}$
D
)A.$-2a^{2}(a^{2}-a + 1)= -2a^{4}+2a^{3}$
B.$(12a^{6}-4a^{3})÷4a^{3}= 3a^{3}$
C.$(a + b)^{2}= a^{2}+b^{2}$
D.$(2a + b)(a + 2b)= 2a^{2}+5ab + 2b^{2}$
答案:
D
4. 下列多项式乘法中,能用完全平方公式计算的是(
A.$(m - n)(-m - n)$
B.$(m + n)(-m + n)$
C.$(m - n)(-m + n)$
D.$(m + 2)(m - 1)$
C
)A.$(m - n)(-m - n)$
B.$(m + n)(-m + n)$
C.$(m - n)(-m + n)$
D.$(m + 2)(m - 1)$
答案:
C
5. 计算:$x^{2}\cdot x^{4}+(-3x^{3})^{2}+(-2x^{2})^{3}= $
$2x^{6}$
.
答案:
$2x^{6}$
6. 已知:$x^{m}= 3$,$x^{n}= 2$,$x^{p}= 6$,$x^{3m + 2n - p}= $
18
.
答案:
18
7. 计算:$(3x^{5}y^{3}-x^{6}y^{2}+x^{4}y^{3}z)÷(-2x^{2}y)^{2}=$
$\frac{3}{4}xy - \frac{1}{4}x^{2} + \frac{1}{4}yz$
.
答案:
$\frac{3}{4}xy - \frac{1}{4}x^{2} + \frac{1}{4}yz$
8. 计算:
(1) $(-a^{2})^{3}÷(-a^{3})^{2}-(-ab^{2})^{3}÷(-b^{2}a)^{3}$;
(2) $(-3mn^{2})^{3}÷(-9m^{2})÷(-n)^{2}$;
(3) $(x - y)^{2}(y - x)^{3}÷(-x + y)^{5}$.
(1) $(-a^{2})^{3}÷(-a^{3})^{2}-(-ab^{2})^{3}÷(-b^{2}a)^{3}$;
(2) $(-3mn^{2})^{3}÷(-9m^{2})÷(-n)^{2}$;
(3) $(x - y)^{2}(y - x)^{3}÷(-x + y)^{5}$.
答案:
解:
(1)$(-a^{2})^{3} ÷ (-a^{3})^{2} - (-ab^{2})^{3} ÷ (-b^{2}a)^{3}$
$=-a^{6} ÷ a^{6} - (-a^{3}b^{6}) ÷ (-a^{3}b^{6})$
$=-1 - 1$
$=-2$
(2)$(-3mn^{2})^{3} ÷ (-9m^{2}) ÷ (-n)^{2}$
$=-27m^{3}n^{6} ÷ (-9m^{2}) ÷ n^{2}$
$=3mn^{6} ÷ n^{2}$
$=3mn^{4}$
(3)$(x - y)^{2} \cdot (y - x)^{3} ÷ (-x + y)^{5}$
$=(y - x)^{2} \cdot (y - x)^{3} ÷ (y - x)^{5}$
$=(y - x)^{5} ÷ (y - x)^{5}$
$=1$
(1)$(-a^{2})^{3} ÷ (-a^{3})^{2} - (-ab^{2})^{3} ÷ (-b^{2}a)^{3}$
$=-a^{6} ÷ a^{6} - (-a^{3}b^{6}) ÷ (-a^{3}b^{6})$
$=-1 - 1$
$=-2$
(2)$(-3mn^{2})^{3} ÷ (-9m^{2}) ÷ (-n)^{2}$
$=-27m^{3}n^{6} ÷ (-9m^{2}) ÷ n^{2}$
$=3mn^{6} ÷ n^{2}$
$=3mn^{4}$
(3)$(x - y)^{2} \cdot (y - x)^{3} ÷ (-x + y)^{5}$
$=(y - x)^{2} \cdot (y - x)^{3} ÷ (y - x)^{5}$
$=(y - x)^{5} ÷ (y - x)^{5}$
$=1$
1. 若 $(3x + m)(3x + n)$ 的结果中不含有 $x$ 项,则 $m$、$n$ 的关系是(
A.$mn = 1$
B.$mn = 0$
C.$m - n = 0$
D.$m + n = 0$
D
)A.$mn = 1$
B.$mn = 0$
C.$m - n = 0$
D.$m + n = 0$
答案:
D
2. 制作拉面需将长方形面条摔匀拉伸后对折,并不断重复.随着不断地对折,面条根数不断增加.若一拉面店一碗面约有 $64$ 根面条,一天能拉出 $2048$ 碗拉面,用底数为 $2$ 的幂表示拉面的总根数为(
A.$2^{6}$
B.$2^{11}$
C.$2^{17}$
D.$2^{66}$
C
)A.$2^{6}$
B.$2^{11}$
C.$2^{17}$
D.$2^{66}$
答案:
C
3. 你能根据下图中图形的面积关系得到的数学公式是(
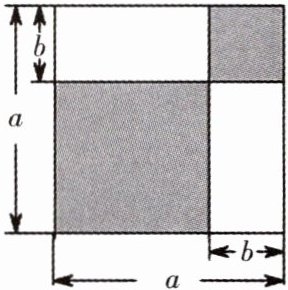
A.$(a + b)(a - b)= a^{2}-b^{2}$
B.$(a + b)^{2}= a^{2}+2ab + b^{2}$
C.$(a - b)^{2}= a^{2}-2ab + b^{2}$
D.$a(a + b)= a^{2}+ab$
C
)
A.$(a + b)(a - b)= a^{2}-b^{2}$
B.$(a + b)^{2}= a^{2}+2ab + b^{2}$
C.$(a - b)^{2}= a^{2}-2ab + b^{2}$
D.$a(a + b)= a^{2}+ab$
答案:
C
4. 已知 $27^{a}×9^{b}= 81$,且 $a\geqslant2b$,则 $8a + 4b$ 的最小值为(
A.$9$
B.$10$
C.$11$
D.$12$
B
)A.$9$
B.$10$
C.$11$
D.$12$
答案:
B
查看更多完整答案,请扫码查看


