8. 如图,在$\triangle ABC$中,有菱形$AMPN$,点$M$、$P$、$N分别在AB$、$BC$、$AC$上。若$\frac{AM}{MB}= \frac{1}{2}$,则$\frac{BP}{BC}= $
$\frac{2}{3}$
.
答案:
解:设$AM = x$,则$MB = 2x$,$AB = AM + MB = 3x$。
因为四边形$AMPN$是菱形,所以$AM = PN = x$,且$AM // PN$。
所以$\angle BMP = \angle A$(两直线平行,同位角相等),$\angle BPM = \angle C$(两直线平行,同位角相等)。
因此$\triangle BMP \sim \triangle BAC$(两角分别相等的两个三角形相似)。
所以$\frac{BP}{BC} = \frac{BM}{BA} = \frac{2x}{3x} = \frac{2}{3}$。
$\frac{2}{3}$
因为四边形$AMPN$是菱形,所以$AM = PN = x$,且$AM // PN$。
所以$\angle BMP = \angle A$(两直线平行,同位角相等),$\angle BPM = \angle C$(两直线平行,同位角相等)。
因此$\triangle BMP \sim \triangle BAC$(两角分别相等的两个三角形相似)。
所以$\frac{BP}{BC} = \frac{BM}{BA} = \frac{2x}{3x} = \frac{2}{3}$。
$\frac{2}{3}$
9. 如图,在梯形$ABCD$中,已知$AD// BC$,$AC$、$BD相交于点O$。若$S_{\triangle AOD}= 4$,$S_{\triangle AOB}= 6$,则$S_{\triangle BOC}= $
9
.
答案:
解:
∵AD//BC,
∴△AOD∽△COB,∠OAD=∠OCB,∠ODA=∠OBC。
∵△AOD与△AOB同高,且S△AOD=4,S△AOB=6,
∴OD/OB=S△AOD/S△AOB=4/6=2/3。
∵△AOD∽△COB,相似比为OD/OB=2/3,
∴S△AOD/S△COB=(2/3)²=4/9。
∵S△AOD=4,
∴4/S△COB=4/9,解得S△COB=9。
即S△BOC=9。
答案:9
∵AD//BC,
∴△AOD∽△COB,∠OAD=∠OCB,∠ODA=∠OBC。
∵△AOD与△AOB同高,且S△AOD=4,S△AOB=6,
∴OD/OB=S△AOD/S△AOB=4/6=2/3。
∵△AOD∽△COB,相似比为OD/OB=2/3,
∴S△AOD/S△COB=(2/3)²=4/9。
∵S△AOD=4,
∴4/S△COB=4/9,解得S△COB=9。
即S△BOC=9。
答案:9
10. 如图,已知$EF// BC$,$FG// CD$.
求证:$\frac{AE}{AB}= \frac{AG}{AD}$.
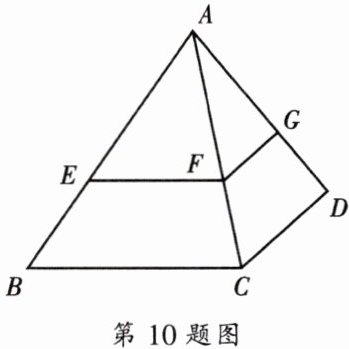
求证:$\frac{AE}{AB}= \frac{AG}{AD}$.

答案:
【解析】:本题可根据平行线分线段成比例定理来证明$\frac{AE}{AB}= \frac{AG}{AD}$。
已知$EF// BC$,根据平行线分线段成比例定理,可得$\frac{AE}{AB}=\frac{AF}{AC}$。
又因为$FG// CD$,同样根据平行线分线段成比例定理,可得$\frac{AG}{AD}=\frac{AF}{AC}$。
由上述两个等式,通过等量代换即可证明$\frac{AE}{AB}= \frac{AG}{AD}$。
【答案】: 证明:
∵$EF// BC$,
∴$\frac{AE}{AB}=\frac{AF}{AC}$(平行线分线段成比例定理)。
∵$FG// CD$,
∴$\frac{AG}{AD}=\frac{AF}{AC}$(平行线分线段成比例定理)。
∴$\frac{AE}{AB}= \frac{AG}{AD}$(等量代换)。
已知$EF// BC$,根据平行线分线段成比例定理,可得$\frac{AE}{AB}=\frac{AF}{AC}$。
又因为$FG// CD$,同样根据平行线分线段成比例定理,可得$\frac{AG}{AD}=\frac{AF}{AC}$。
由上述两个等式,通过等量代换即可证明$\frac{AE}{AB}= \frac{AG}{AD}$。
【答案】: 证明:
∵$EF// BC$,
∴$\frac{AE}{AB}=\frac{AF}{AC}$(平行线分线段成比例定理)。
∵$FG// CD$,
∴$\frac{AG}{AD}=\frac{AF}{AC}$(平行线分线段成比例定理)。
∴$\frac{AE}{AB}= \frac{AG}{AD}$(等量代换)。
11. 如图,在$\triangle ABC$中,已知$DG// EC$,$EG// BC$.
求证:$AE^{2}= AB\cdot AD$.
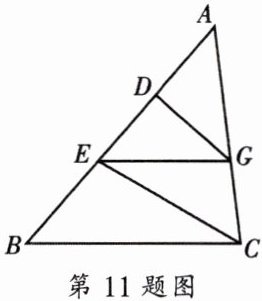
求证:$AE^{2}= AB\cdot AD$.

答案:
【解析】:本题主要考查平行线分线段成比例定理及相似三角形的判定与性质。
已知$DG// EC$,$EG// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,因为$DG// EC$,所以有$\frac{AD}{AE}=\frac{AG}{AC}$ ①;
又因为$EG// BC$,所以可得$\frac{AG}{AC}=\frac{AE}{AB}$ ②;
由①②可得$\frac{AD}{AE}=\frac{AE}{AB}$,根据比例的基本性质“两外项之积等于两内项之积”,就可以证明$AE^{2}=AB\cdot AD$。
【答案】:证明:
∵$DG// EC$,
∴$\frac{AD}{AE}=\frac{AG}{AC}$,
∵$EG// BC$,
∴$\frac{AG}{AC}=\frac{AE}{AB}$,
∴$\frac{AD}{AE}=\frac{AE}{AB}$,
∴$AE^{2}=AB\cdot AD$。
已知$DG// EC$,$EG// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,因为$DG// EC$,所以有$\frac{AD}{AE}=\frac{AG}{AC}$ ①;
又因为$EG// BC$,所以可得$\frac{AG}{AC}=\frac{AE}{AB}$ ②;
由①②可得$\frac{AD}{AE}=\frac{AE}{AB}$,根据比例的基本性质“两外项之积等于两内项之积”,就可以证明$AE^{2}=AB\cdot AD$。
【答案】:证明:
∵$DG// EC$,
∴$\frac{AD}{AE}=\frac{AG}{AC}$,
∵$EG// BC$,
∴$\frac{AG}{AC}=\frac{AE}{AB}$,
∴$\frac{AD}{AE}=\frac{AE}{AB}$,
∴$AE^{2}=AB\cdot AD$。
12. 如图,已知四边形$ABCD$是平行四边形,$E是AB$延长线上一点,$DE分别交对角线AC于点G$,边$BC于点F$.
(1)求证:$DG^{2}= GF\cdot GE$;
(2)求证:$\frac{GC^{2}}{GA^{2}}= \frac{GF}{GE}$.
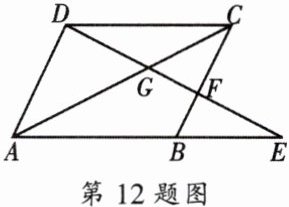
(1)求证:$DG^{2}= GF\cdot GE$;
(2)求证:$\frac{GC^{2}}{GA^{2}}= \frac{GF}{GE}$.

答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD,AD=BC,AB=CD。
∵AD//BC,
∴∠ADG=∠GFC,∠DAG=∠GCF,
∴△ADG∽△CFG,
∴$\frac{DG}{GF}=\frac{AG}{GC}$。
∵AB//CD,
∴∠DCG=∠EAG,∠CDG=∠AEG,
∴△CDG∽△AEG,
∴$\frac{GC}{GA}=\frac{DG}{GE}$,即$\frac{AG}{GC}=\frac{GE}{DG}$。
∴$\frac{DG}{GF}=\frac{GE}{DG}$,
∴$DG^2=GF\cdot GE$。
(2)证明:
由
(1)知$\frac{DG}{GF}=\frac{AG}{GC}$且$\frac{GC}{GA}=\frac{DG}{GE}$,
∴$\frac{DG}{GF}\cdot\frac{DG}{GE}=\frac{AG}{GC}\cdot\frac{GC}{GA}=1$,
即$\frac{DG^2}{GF\cdot GE}=1$,又由
(1)得$DG^2=GF\cdot GE$,代入得$\frac{GF\cdot GE}{GF\cdot GE}=1$(恒成立)。
由$\frac{DG}{GF}=\frac{AG}{GC}$得$\frac{GF}{DG}=\frac{GC}{AG}$,
由$\frac{DG}{GE}=\frac{GC}{GA}$得$\frac{DG}{GE}=\frac{GC}{GA}$,
两式相乘:$\frac{GF}{DG}\cdot\frac{DG}{GE}=\frac{GC}{AG}\cdot\frac{GC}{GA}$,
∴$\frac{GF}{GE}=\frac{GC^2}{GA^2}$,
即$\frac{GC^2}{GA^2}=\frac{GF}{GE}$。
(1)证明:
∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD,AD=BC,AB=CD。
∵AD//BC,
∴∠ADG=∠GFC,∠DAG=∠GCF,
∴△ADG∽△CFG,
∴$\frac{DG}{GF}=\frac{AG}{GC}$。
∵AB//CD,
∴∠DCG=∠EAG,∠CDG=∠AEG,
∴△CDG∽△AEG,
∴$\frac{GC}{GA}=\frac{DG}{GE}$,即$\frac{AG}{GC}=\frac{GE}{DG}$。
∴$\frac{DG}{GF}=\frac{GE}{DG}$,
∴$DG^2=GF\cdot GE$。
(2)证明:
由
(1)知$\frac{DG}{GF}=\frac{AG}{GC}$且$\frac{GC}{GA}=\frac{DG}{GE}$,
∴$\frac{DG}{GF}\cdot\frac{DG}{GE}=\frac{AG}{GC}\cdot\frac{GC}{GA}=1$,
即$\frac{DG^2}{GF\cdot GE}=1$,又由
(1)得$DG^2=GF\cdot GE$,代入得$\frac{GF\cdot GE}{GF\cdot GE}=1$(恒成立)。
由$\frac{DG}{GF}=\frac{AG}{GC}$得$\frac{GF}{DG}=\frac{GC}{AG}$,
由$\frac{DG}{GE}=\frac{GC}{GA}$得$\frac{DG}{GE}=\frac{GC}{GA}$,
两式相乘:$\frac{GF}{DG}\cdot\frac{DG}{GE}=\frac{GC}{AG}\cdot\frac{GC}{GA}$,
∴$\frac{GF}{GE}=\frac{GC^2}{GA^2}$,
即$\frac{GC^2}{GA^2}=\frac{GF}{GE}$。
查看更多完整答案,请扫码查看


