10. 平行于三角形一边的直线被其他两边所截得的线段叫做“三角形的弦”,事实上,三角形的中位线就可以看作三角形的一条弦. 已知等边三角形的边长为$2$, 若一条弦将该等边三角形的面积分为相等的两个部分,则这条弦的长为
$\sqrt{2}$
.
答案:
$\sqrt{2}$
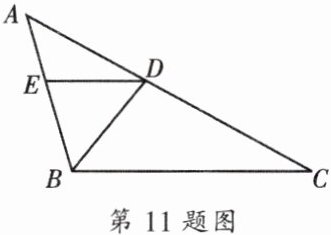
11. 如图,在$\triangle ABC$中,已知$BD是\angle ABC$的平分线,过点$D作DE// CB$,交$AB于点E$,$\triangle ADE与\triangle ACB的面积之比为1:16$.
(1)求$AE:EB$;
(2)求$S_{\triangle ADE}:S_{\triangle BDE}$;
(3)求$S_{\triangle ADE}:S_{\triangle BCD}$.
(1)求$AE:EB$;
(2)求$S_{\triangle ADE}:S_{\triangle BDE}$;
(3)求$S_{\triangle ADE}:S_{\triangle BCD}$.

答案:
【解析】:本题主要考查相似三角形的性质以及面积比的计算。
(1)求$AE:EB$:
由于$\triangle ADE \sim \triangle ACB$(因为$DE // CB$,所以对应角相等,从而相似),且它们的面积之比为$1:16$。
根据相似三角形的性质,面积之比等于相似比的平方,即:
$\frac{S_{\triangle ADE}}{S_{\triangle ACB}} = \left(\frac{AE}{AB}\right)^2 = \frac{1}{16}$,
解得:
$\frac{AE}{AB} = \frac{1}{4}$,
设$AE = x$,则$AB = 4x$,所以:
$EB = AB - AE = 4x - x = 3x$,
因此,$AE:EB = x:3x = 1:3$。
(2)求$S_{\triangle ADE}:S_{\triangle BDE}$:
由于$\triangle ADE$和$\triangle BDE$在$DE$边上的高是相同的,所以它们的面积之比等于底边之比,即:
$\frac{S_{\triangle ADE}}{S_{\triangle BDE}} = \frac{AE}{EB} = \frac{1}{3}$。
(3)求$S_{\triangle ADE}:S_{\triangle BCD}$:
由于$BD$是$\angle ABC$的平分线,且$DE // CB$,根据平行线和角平分线的性质,我们可以得出$\triangle BDE$是等腰三角形,即$BE = DE$。
设$S_{\triangle ADE} = a$,则$S_{\triangle BDE} = 3a$(由
(2)得出)。
由于$\triangle BDE$和$\triangle BCD$在$BD$边上的高之比等于$DE$与$CB$之比,也即$AE$与$AB$之比(因为$DE // CB$),所以:
$\frac{S_{\triangle BDE}}{S_{\triangle BCD}} = \frac{DE}{CB} = \frac{AE}{AB} = \frac{1}{4}$,
从而$S_{\triangle BCD} = 4 × S_{\triangle BDE} = 4 × 3a = 12a$。
因此,$S_{\triangle ADE}:S_{\triangle BCD} = a:12a = 1:12$。
【答案】:
(1)$AE:EB = 1:3$;
(2)$S_{\triangle ADE}:S_{\triangle BDE} = 1:3$;
(3)$S_{\triangle ADE}:S_{\triangle BCD} = 1:12$。
(1)求$AE:EB$:
由于$\triangle ADE \sim \triangle ACB$(因为$DE // CB$,所以对应角相等,从而相似),且它们的面积之比为$1:16$。
根据相似三角形的性质,面积之比等于相似比的平方,即:
$\frac{S_{\triangle ADE}}{S_{\triangle ACB}} = \left(\frac{AE}{AB}\right)^2 = \frac{1}{16}$,
解得:
$\frac{AE}{AB} = \frac{1}{4}$,
设$AE = x$,则$AB = 4x$,所以:
$EB = AB - AE = 4x - x = 3x$,
因此,$AE:EB = x:3x = 1:3$。
(2)求$S_{\triangle ADE}:S_{\triangle BDE}$:
由于$\triangle ADE$和$\triangle BDE$在$DE$边上的高是相同的,所以它们的面积之比等于底边之比,即:
$\frac{S_{\triangle ADE}}{S_{\triangle BDE}} = \frac{AE}{EB} = \frac{1}{3}$。
(3)求$S_{\triangle ADE}:S_{\triangle BCD}$:
由于$BD$是$\angle ABC$的平分线,且$DE // CB$,根据平行线和角平分线的性质,我们可以得出$\triangle BDE$是等腰三角形,即$BE = DE$。
设$S_{\triangle ADE} = a$,则$S_{\triangle BDE} = 3a$(由
(2)得出)。
由于$\triangle BDE$和$\triangle BCD$在$BD$边上的高之比等于$DE$与$CB$之比,也即$AE$与$AB$之比(因为$DE // CB$),所以:
$\frac{S_{\triangle BDE}}{S_{\triangle BCD}} = \frac{DE}{CB} = \frac{AE}{AB} = \frac{1}{4}$,
从而$S_{\triangle BCD} = 4 × S_{\triangle BDE} = 4 × 3a = 12a$。
因此,$S_{\triangle ADE}:S_{\triangle BCD} = a:12a = 1:12$。
【答案】:
(1)$AE:EB = 1:3$;
(2)$S_{\triangle ADE}:S_{\triangle BDE} = 1:3$;
(3)$S_{\triangle ADE}:S_{\triangle BCD} = 1:12$。
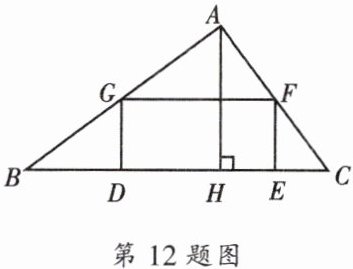
12. 如图,已知在$\triangle ABC$中,$BC为60$,边$BC上的高AH为40$;矩形$DEFG的顶点D$、$E在边BC$上,顶点$G$、$F分别在边AB$、$AC$上. 设$EF的长为x$.
(1)用含$x的代数式表示矩形DEFG$的面积;
(2)当矩形$DEFG$成为正方形时,求相应的$x$值.
(1)用含$x的代数式表示矩形DEFG$的面积;
(2)当矩形$DEFG$成为正方形时,求相应的$x$值.

答案:
(1)解:设矩形DEFG的边DG=EF=x,DE=GF=y。
∵GF//BC,
∴△AGF∽△ABC。
∵AH⊥BC,
∴AH=40,GF=x,BC=60。
设GF到A的距离为h,则h=AH - DG=40 - y。
由相似三角形性质:$\frac{h}{AH}=\frac{GF}{BC}$,即$\frac{40 - y}{40}=\frac{x}{60}$。
解得$y=40 - \frac{2}{3}x$。
矩形面积$S=xy=x(40 - \frac{2}{3}x)=-\frac{2}{3}x^2 + 40x$。
(2)解:当矩形为正方形时,x=y。
由
(1)知$y=40 - \frac{2}{3}x$,则$x=40 - \frac{2}{3}x$。
解得$x=24$。
答:
(1)矩形面积为$-\frac{2}{3}x^2 + 40x$;
(2)x的值为24。
(1)解:设矩形DEFG的边DG=EF=x,DE=GF=y。
∵GF//BC,
∴△AGF∽△ABC。
∵AH⊥BC,
∴AH=40,GF=x,BC=60。
设GF到A的距离为h,则h=AH - DG=40 - y。
由相似三角形性质:$\frac{h}{AH}=\frac{GF}{BC}$,即$\frac{40 - y}{40}=\frac{x}{60}$。
解得$y=40 - \frac{2}{3}x$。
矩形面积$S=xy=x(40 - \frac{2}{3}x)=-\frac{2}{3}x^2 + 40x$。
(2)解:当矩形为正方形时,x=y。
由
(1)知$y=40 - \frac{2}{3}x$,则$x=40 - \frac{2}{3}x$。
解得$x=24$。
答:
(1)矩形面积为$-\frac{2}{3}x^2 + 40x$;
(2)x的值为24。
查看更多完整答案,请扫码查看


