1. 下列各命题中,是真命题的是 (
A.全等三角形都相似;
B.有一个角为$50^{\circ }$的两个等腰三角形一定相似;
C.有两条边成比例的两个直角三角形一定相似;
D.有两条边成比例的两个等腰三角形一定相似.
A
)A.全等三角形都相似;
B.有一个角为$50^{\circ }$的两个等腰三角形一定相似;
C.有两条边成比例的两个直角三角形一定相似;
D.有两条边成比例的两个等腰三角形一定相似.
答案:
【解析】:
本题主要考察相似三角形的判定定理。
A选项:全等三角形都相似。根据相似三角形的定义,如果两个三角形的对应角都相等,则这两个三角形相似。全等三角形的所有对应角都相等,因此全等三角形都相似。所以A选项是真命题。
B选项:有一个角为$50^{\circ}$的两个等腰三角形一定相似。考虑等腰三角形的性质,如果一个等腰三角形的一个角为$50^{\circ}$,那么它的另一个底角也为$50^{\circ}$,顶角为$80^{\circ}$;或者两个底角都为$65^{\circ}$,顶角为$50^{\circ}$。因此,存在两种可能的等腰三角形,它们的角度并不完全相同,所以不一定相似。故B选项是假命题。
C选项:有两条边成比例的两个直角三角形一定相似。考虑直角三角形的性质,除了直角外,还有两个锐角。即使两个直角三角形的两条边成比例,它们的对应角也不一定都相等(特别是锐角),因此不一定相似。故C选项是假命题。
D选项:有两条边成比例的两个等腰三角形一定相似。等腰三角形有两边相等,但如果只知道有两条边成比例,并不能确定这两个等腰三角形的对应角都相等。例如,一个等腰三角形的底角为$72^{\circ}$,顶角为$36^{\circ}$;另一个等腰三角形的底角为$36^{\circ}$,顶角为$108^{\circ}$。这两个等腰三角形的两边虽然可能成比例,但它们的对应角并不都相等,因此不一定相似。故D选项是假命题。
【答案】:
A
本题主要考察相似三角形的判定定理。
A选项:全等三角形都相似。根据相似三角形的定义,如果两个三角形的对应角都相等,则这两个三角形相似。全等三角形的所有对应角都相等,因此全等三角形都相似。所以A选项是真命题。
B选项:有一个角为$50^{\circ}$的两个等腰三角形一定相似。考虑等腰三角形的性质,如果一个等腰三角形的一个角为$50^{\circ}$,那么它的另一个底角也为$50^{\circ}$,顶角为$80^{\circ}$;或者两个底角都为$65^{\circ}$,顶角为$50^{\circ}$。因此,存在两种可能的等腰三角形,它们的角度并不完全相同,所以不一定相似。故B选项是假命题。
C选项:有两条边成比例的两个直角三角形一定相似。考虑直角三角形的性质,除了直角外,还有两个锐角。即使两个直角三角形的两条边成比例,它们的对应角也不一定都相等(特别是锐角),因此不一定相似。故C选项是假命题。
D选项:有两条边成比例的两个等腰三角形一定相似。等腰三角形有两边相等,但如果只知道有两条边成比例,并不能确定这两个等腰三角形的对应角都相等。例如,一个等腰三角形的底角为$72^{\circ}$,顶角为$36^{\circ}$;另一个等腰三角形的底角为$36^{\circ}$,顶角为$108^{\circ}$。这两个等腰三角形的两边虽然可能成比例,但它们的对应角并不都相等,因此不一定相似。故D选项是假命题。
【答案】:
A
2. 已知$△ABC$的三边长分别为6,7.5,9,$△DEF$的一边长为5. 若这两个三角形相似,则$△DEF$的另两边长应为 (
A.2,3;
B.4,6;
C.6,7;
D.7,9.
B
)A.2,3;
B.4,6;
C.6,7;
D.7,9.
答案:
【解析】:
本题考查的是相似三角形的性质,即相似三角形的对应边之间的比例是相等的。
首先,我们观察$△ABC$的三边长,分别为6,7.5,9,可以发现它们之间的比例是2:2.5:3,简化后得到4:5:6。
接着,我们来看$△DEF$,已知其中一边长为5,需要找出与这条边相似的$△ABC$中的边。
如果5与6是对应边,那么比例因子是$\frac{5}{6}$,但此时其他两边计算出的结果并不在选项中。
如果5与7.5是对应边,那么比例因子是$\frac{5}{7.5} = \frac{2}{3}$,此时另外两条边应为$6 × \frac{2}{3} = 4$和$9 × \frac{2}{3} = 6$,这两个数构成的边长组合是选项B。
如果5与9是对应边,那么比例因子是$\frac{5}{9}$,但此时其他两边计算出的结果也不在选项中。
因此,我们可以确定$△DEF$的另两边长应为4和6。
【答案】:
B. 4,6。
本题考查的是相似三角形的性质,即相似三角形的对应边之间的比例是相等的。
首先,我们观察$△ABC$的三边长,分别为6,7.5,9,可以发现它们之间的比例是2:2.5:3,简化后得到4:5:6。
接着,我们来看$△DEF$,已知其中一边长为5,需要找出与这条边相似的$△ABC$中的边。
如果5与6是对应边,那么比例因子是$\frac{5}{6}$,但此时其他两边计算出的结果并不在选项中。
如果5与7.5是对应边,那么比例因子是$\frac{5}{7.5} = \frac{2}{3}$,此时另外两条边应为$6 × \frac{2}{3} = 4$和$9 × \frac{2}{3} = 6$,这两个数构成的边长组合是选项B。
如果5与9是对应边,那么比例因子是$\frac{5}{9}$,但此时其他两边计算出的结果也不在选项中。
因此,我们可以确定$△DEF$的另两边长应为4和6。
【答案】:
B. 4,6。
3. 如图,在$△ABC$中,已知点D在边AB上,且$∠ACD= ∠B$,过点A作$AE// CB$交CD的延长线于点E,则图中相似三角形共有
3
对.
答案:
解:
1. 在$△ACD$和$△ABC$中,
$\because ∠ACD=∠B$,$∠A=∠A$(公共角),
$\therefore △ACD \backsim △ABC$(两角对应相等,两三角形相似)。
2. $\because AE // CB$,
$\therefore ∠E=∠BCD$(两直线平行,内错角相等)。
在$△ADE$和$△BDC$中,
$\because ∠E=∠BCD$,$∠ADE=∠BDC$(对顶角相等),
$\therefore △ADE \backsim △BDC$(两角对应相等,两三角形相似)。
3. $\because AE // CB$,
$\therefore ∠EAB=∠B$(两直线平行,同位角相等)。
又$\because ∠ACD=∠B$,
$\therefore ∠EAB=∠ACD$。
在$△AEC$和$△DEA$中,
$\because ∠E=∠E$(公共角),$∠EAB=∠ACD$,
$\therefore △AEC \backsim △DEA$(两角对应相等,两三角形相似)。
综上,图中相似三角形共有3对。
答案:3
1. 在$△ACD$和$△ABC$中,
$\because ∠ACD=∠B$,$∠A=∠A$(公共角),
$\therefore △ACD \backsim △ABC$(两角对应相等,两三角形相似)。
2. $\because AE // CB$,
$\therefore ∠E=∠BCD$(两直线平行,内错角相等)。
在$△ADE$和$△BDC$中,
$\because ∠E=∠BCD$,$∠ADE=∠BDC$(对顶角相等),
$\therefore △ADE \backsim △BDC$(两角对应相等,两三角形相似)。
3. $\because AE // CB$,
$\therefore ∠EAB=∠B$(两直线平行,同位角相等)。
又$\because ∠ACD=∠B$,
$\therefore ∠EAB=∠ACD$。
在$△AEC$和$△DEA$中,
$\because ∠E=∠E$(公共角),$∠EAB=∠ACD$,
$\therefore △AEC \backsim △DEA$(两角对应相等,两三角形相似)。
综上,图中相似三角形共有3对。
答案:3
4. 如图,在$△ABC$中,$∠ACB$的平分线交AB于点D,过D作BC的平行线交AC于点E.若$AC= 6$,$BC= 12$,则DE的长等于______

4
.
答案:
解:
∵ CD平分∠ACB,
∴ ∠ACD=∠BCD。
∵ DE//BC,
∴ ∠EDC=∠BCD,∠AED=∠ACB,∠ADE=∠ABC。
∴ ∠EDC=∠ACD,
∴ DE=EC。
∵ DE//BC,
∴ △ADE∽△ABC。
∴ $\frac{AE}{AC}=\frac{DE}{BC}$。
设DE=EC=x,
∵ AC=6,
∴ AE=AC-EC=6-x。
∵ BC=12,
∴ $\frac{6-x}{6}=\frac{x}{12}$。
解得x=4。
∴ DE=4。
答案:4
∵ CD平分∠ACB,
∴ ∠ACD=∠BCD。
∵ DE//BC,
∴ ∠EDC=∠BCD,∠AED=∠ACB,∠ADE=∠ABC。
∴ ∠EDC=∠ACD,
∴ DE=EC。
∵ DE//BC,
∴ △ADE∽△ABC。
∴ $\frac{AE}{AC}=\frac{DE}{BC}$。
设DE=EC=x,
∵ AC=6,
∴ AE=AC-EC=6-x。
∵ BC=12,
∴ $\frac{6-x}{6}=\frac{x}{12}$。
解得x=4。
∴ DE=4。
答案:4
5. 如图,在已建立平面直角坐标系的$4×4$正方形方格纸中,画格点三角形ABC(三角形的三个顶点都是小正方形的顶点).若以格点P、A、B为顶点的三角形与$△ABC$相似(全等除外),则格点P的坐标是
(1,2)或(3,2)
.
答案:
解:由图可知,A(1,0),B(3,0),C(1,1)。
计算得:AB=2,AC=1,BC=$\sqrt{(3-1)^2+(0-1)^2}=\sqrt{5}$。
设P(x,y),以P、A、B为顶点的三角形与△ABC相似(全等除外)。
分情况讨论:
1. 当$\frac{PA}{AC}=\frac{PB}{BC}=\frac{AB}{AB}=1$时,为全等三角形,舍去。
2. 当$\frac{PA}{BC}=\frac{PB}{AC}=\frac{AB}{AB}=1$时,PA=$\sqrt{5}$,PB=1。
解得P(1,2),此时△PAB∽△CBA。
3. 当$\frac{PA}{AB}=\frac{PB}{BC}=\frac{AB}{AC}=2$时,PA=4,PB=2$\sqrt{5}$。
解得P(3,2),此时△PAB∽△ACB。
格点P的坐标是(1,2)或(3,2)。
计算得:AB=2,AC=1,BC=$\sqrt{(3-1)^2+(0-1)^2}=\sqrt{5}$。
设P(x,y),以P、A、B为顶点的三角形与△ABC相似(全等除外)。
分情况讨论:
1. 当$\frac{PA}{AC}=\frac{PB}{BC}=\frac{AB}{AB}=1$时,为全等三角形,舍去。
2. 当$\frac{PA}{BC}=\frac{PB}{AC}=\frac{AB}{AB}=1$时,PA=$\sqrt{5}$,PB=1。
解得P(1,2),此时△PAB∽△CBA。
3. 当$\frac{PA}{AB}=\frac{PB}{BC}=\frac{AB}{AC}=2$时,PA=4,PB=2$\sqrt{5}$。
解得P(3,2),此时△PAB∽△ACB。
格点P的坐标是(1,2)或(3,2)。
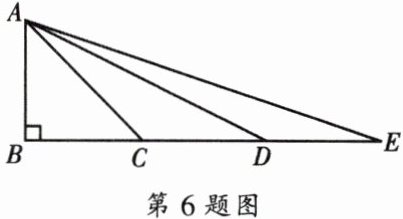
6. 如图,已知在$△ABC$中,$∠ABC= 90^{\circ },AB= BC$,延长BC到点E,使得$CE= 2BC$,取CE的中点D,联结AE、AD. 求证:$△ACD\backsim △ECA$.

答案:
证明:设 $ BC = x $,
∵ $ AB = BC $,$ ∠ABC = 90^\circ $,
∴ $ AB = x $,$ AC = \sqrt{AB^2 + BC^2} = \sqrt{x^2 + x^2} = \sqrt{2}x $。
∵ $ CE = 2BC $,
∴ $ CE = 2x $,$ BE = BC + CE = 3x $。
∵ $ D $ 是 $ CE $ 中点,
∴ $ CD = DE = \frac{1}{2}CE = x $,$ BD = BC + CD = 2x $。
在 $ \triangle ACD $ 和 $ \triangle ECA $ 中:
$ AC = \sqrt{2}x $,$ CD = x $,$ CE = 2x $,
∴ $ \frac{AC}{CE} = \frac{\sqrt{2}x}{2x} = \frac{\sqrt{2}}{2} $,
$ \frac{CD}{AC} = \frac{x}{\sqrt{2}x} = \frac{\sqrt{2}}{2} $,
即 $ \frac{AC}{CE} = \frac{CD}{AC} $。
又 $ ∠ACD = ∠ECA $(公共角),
∴ $ \triangle ACD \backsim \triangle ECA $(两边对应成比例且夹角相等的两个三角形相似)。
∵ $ AB = BC $,$ ∠ABC = 90^\circ $,
∴ $ AB = x $,$ AC = \sqrt{AB^2 + BC^2} = \sqrt{x^2 + x^2} = \sqrt{2}x $。
∵ $ CE = 2BC $,
∴ $ CE = 2x $,$ BE = BC + CE = 3x $。
∵ $ D $ 是 $ CE $ 中点,
∴ $ CD = DE = \frac{1}{2}CE = x $,$ BD = BC + CD = 2x $。
在 $ \triangle ACD $ 和 $ \triangle ECA $ 中:
$ AC = \sqrt{2}x $,$ CD = x $,$ CE = 2x $,
∴ $ \frac{AC}{CE} = \frac{\sqrt{2}x}{2x} = \frac{\sqrt{2}}{2} $,
$ \frac{CD}{AC} = \frac{x}{\sqrt{2}x} = \frac{\sqrt{2}}{2} $,
即 $ \frac{AC}{CE} = \frac{CD}{AC} $。
又 $ ∠ACD = ∠ECA $(公共角),
∴ $ \triangle ACD \backsim \triangle ECA $(两边对应成比例且夹角相等的两个三角形相似)。
查看更多完整答案,请扫码查看


