《2025年中学生世界九年级数学上册沪教版五四制》

1. 已知$\triangle ABC \backsim \triangle DEF$,$\triangle ABC的三边长之比为3:4:5$,$\triangle DEF最短边的长为6cm$,则$\triangle DEF$的最长边为(C)
A.$8cm$；
B.$9cm$；
C.$10cm$；
D.$12cm$。

答案： 【解析】：
本题主要考察相似三角形的性质，即相似三角形的对应边之间的比例是相等的。
已知$\triangle ABC \backsim \triangle DEF$，且$\triangle ABC$的三边长之比为$3:4:5$，$\triangle DEF$的最短边长为$6cm$。
根据相似三角形的性质，设$\triangle DEF$的最长边为$x$，我们可以得到比例关系：
$\frac{\text{最短边} \triangle ABC}{\text{最短边} \triangle DEF} = \frac{\text{最长边} \triangle ABC}{\text{最长边} \triangle DEF}$，
即$\frac{3}{6} = \frac{5}{x}$，
解这个比例式，我们得到$x = 10$。
【答案】：C. $10cm$。

2. 如果两个相似三角形对应边长之比是$1:4$,那么它们的对应中线长之比是(B)
A.$1:2$；
B.$1:4$；
C.$1:8$；
D.$1:16$。

答案： 解：
∵相似三角形对应中线长之比等于相似比，
又
∵两个相似三角形对应边长之比是1:4，即相似比为1:4，
∴它们的对应中线长之比是1:4。
答案：B

3. 在$\triangle ABC$中,已知$BC = 15cm$,$CA = 55cm$,$AB = 63cm$,另一个和它相似的三角形的最短边长是$5cm$,则这个三角形的最长边长是(B)
A.$18cm$；
B.$21cm$；
C.$24cm$；
D.$19.5cm$。

答案： 【解析】：
本题主要考察相似三角形的性质，即相似三角形的对应边之间的比例是相等的。
首先，我们需要确定原三角形$\triangle ABC$中的最短边和最长边。
由题意知，$BC = 15cm$是最短边，$AB = 63cm$是最长边。
另一个和它相似的三角形的最短边长是$5cm$，设这个三角形的最长边长为$x cm$。
根据相似三角形的性质，我们有：
$\frac{原三角形的最短边}{相似三角形的最短边} = \frac{原三角形的最长边}{相似三角形的最长边}$
即：
$\frac{15}{5} = \frac{63}{x}$
解这个方程，我们得到：
$x = \frac{63 × 5}{15} = 21(cm)$
所以，这个相似三角形的最长边长是$21cm$。
【答案】：B. $21cm$。

4. 如图,已知$AD // BC$,$\angle D = 90^{\circ}$,$DC = 7$,$AD = 2$,$BC = 4$。若在边$DC上有点P$,使$\triangle PAD和\triangle PBC$相似,则这样的点$P$有(C)
A.$1$个；
B.$2$个；
C.$3$个；
D.$4$个。

答案： 【解析】：本题可根据相似三角形的性质，分两种情况讨论$\triangle PAD$与$\triangle PBC$相似时点$P$的位置。
已知$AD// BC$，$\angle D = 90^{\circ}$，则$\angle C = 90^{\circ}$。
设$DP = x$，则$PC = 7 - x$。
情况一：当$\triangle PAD\sim\triangle PBC$时
根据相似三角形对应边成比例的性质，可得$\frac{AD}{PC}=\frac{DP}{BC}$。
已知$AD = 2$，$BC = 4$，$DP = x$，$PC = 7 - x$，代入上式可得：
$\frac{2}{7 - x}=\frac{x}{4}$
交叉相乘得到：$x(7 - x)=2×4$
即$x^{2}-7x + 8 = 0$。
对于一元二次方程$ax^{2}+bx+c=0(a\neq0)$，其判别式$\Delta=b^{2}-4ac$，在方程$x^{2}-7x + 8 = 0$中，$a = 1$，$b = -7$，$c = 8$，则$\Delta=(-7)^{2}-4×1×8=49 - 32 = 17\gt0$，所以此方程有两个不同的实数解，即这种情况下有$2$个点$P$满足条件。
情况二：当$\triangle PAD\sim\triangle CPB$时
根据相似三角形对应边成比例的性质，可得$\frac{AD}{BC}=\frac{DP}{PC}$。
将$AD = 2$，$BC = 4$，$DP = x$，$PC = 7 - x$代入可得：
$\frac{2}{4}=\frac{x}{7 - x}$
交叉相乘得到：$2(7 - x)=4x$
去括号得：$14 - 2x = 4x$
移项可得：$4x + 2x = 14$
合并同类项得：$6x = 14$
解得：$x=\frac{7}{3}$，即这种情况下有$1$个点$P$满足条件。
综合以上两种情况，满足$\triangle PAD$和$\triangle PBC$相似的点$P$共有$2 + 1 = 3$个。
【答案】：C。

5. 若两个相似三角形的相似比为$1:4$,则这两个三角形的对应边上的高之比为$1:4$,对应角的平分线长之比为$1:4$。

答案： 【解析】：
本题考查相似三角形的性质。
对于两个相似三角形，如果它们的相似比为$a:b$，那么它们的对应边上的高之比、对应角的平分线长之比、对应中线之比等都等于它们的相似比。
在本题中，已知两个相似三角形的相似比为$1:4$，所以可以直接得出：
这两个三角形的对应边上的高之比也为$1:4$；
对应角的平分线长之比也为$1:4$。
【答案】：
$1:4$；$1:4$。

6. 如图,在$\triangle ABC$中,已知$DE // BC$,$DE分别与AB$、$AC相交于点D$、$E$,$AD:AB = 1:3$。若$DE = 2$,则$BC = $6。

答案： 【解析】：本题主要考查相似三角形的性质。
由于$DE// BC$，
根据平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似，
所以$\triangle ADE\sim\triangle ABC$。
已知$\frac{AD}{AB}=\frac{1}{3}$，
根据相似三角形的性质，相似三角形对应边成比例，
所以$\frac{DE}{BC}=\frac{AD}{AB}=\frac{1}{3}$。
已知$DE=2$，代入$\frac{DE}{BC}=\frac{1}{3}$，
得到$\frac{2}{BC}=\frac{1}{3}$，
解这个方程，得到$BC=6$。
【答案】：$BC=6$。

7. 已知在$\triangle ABC$中,$AB = 20$,$AC = 12$,$BC = 16$,$D是射线BC$上的一点(不与端点$B$重合),联结$AD$。如果$\triangle ACD与\triangle ABC$相似,那么$BD = $7或$\frac{128}{5}$。

答案： 1. 首先判断$\triangle ABC$的形状：
计算$AC^{2}+BC^{2}$和$AB^{2}$的值：
已知$AB = 20$，$AC = 12$，$BC = 16$，则$AC^{2}+BC^{2}=12^{2}+16^{2}=144 + 256=400$，$AB^{2}=20^{2}=400$。
所以$AC^{2}+BC^{2}=AB^{2}$，根据勾股定理逆定理，$\angle C = 90^{\circ}$。
2. 然后分情况讨论$\triangle ACD$与$\triangle ABC$相似：
情况一：当$\triangle ACD\sim\triangle BCA$时：
根据相似三角形的性质，$\frac{AC}{BC}=\frac{CD}{CA}$。
已知$AC = 12$，$BC = 16$，设$CD=x$，则$\frac{12}{16}=\frac{x}{12}$。
交叉相乘得$16x=12×12$，即$x = 9$。
因为$BD=BC - CD$，所以$BD=16 - 9 = 7$。
情况二：当$\triangle ACD\sim\triangle ACB$时：
根据相似三角形的性质，$\frac{AC}{AC}=\frac{CD}{CB}$（此时$CD = CB$不满足$D$不与端点$B$重合，舍去）；当$\triangle ACD\sim\triangle ABC$时，$\frac{AC}{AB}=\frac{CD}{BC}$。
设$CD = y$，已知$AC = 12$，$AB = 20$，$BC = 16$，则$\frac{12}{20}=\frac{y}{16}$。
交叉相乘得$20y=12×16$，$y=\frac{12×16}{20}=\frac{48}{5}$。
此时$BD=BC + CD$（$D$在$BC$的延长线上），$BD=16+\frac{48}{5}=\frac{80 + 48}{5}=\frac{128}{5}$。
综上，$BD$的值为$7$或$\frac{128}{5}$。

8. 在$\triangle ABC和\triangle DEF$中,若$\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}$,且$\angle A = 45^{\circ}$,则$\angle D = $$45^{\circ}$。

答案： 解：因为在$\triangle ABC$和$\triangle DEF$中，$\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}$，所以$\triangle ABC \sim \triangle DEF$（三边成比例的两个三角形相似）。
由于相似三角形的对应角相等，且$\angle A$与$\angle D$是对应角，已知$\angle A = 45^{\circ}$，所以$\angle D = 45^{\circ}$。
$45^{\circ}$

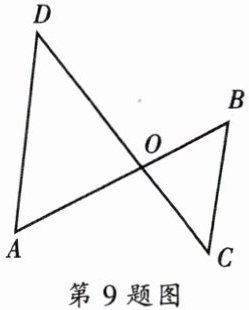
9. 如图,已知$AB$、$CD相交于点O$,且$\angle A = \angle C$。若$OA = 6$,$OD = 8$,$OB = 4$,则$OC = $3。

答案： 【解析】：
本题主要考查相似三角形的性质，即相似三角形对应边成比例，由已知条件$AB$，$CD$相交于点$O$，且$\angle A=\angle C$，可以发现$\bigtriangleup AOD$和$\bigtriangleup COB$中，$\angle AOD=\angle COB$（对顶角相等），$\angle A=\angle C$，所以根据相似三角形的判定定理（两角分别相等的两个三角形相似）可得$\bigtriangleup AOD\sim\bigtriangleup COB$，再根据相似三角形对应边成比例列出比例式，最后代入已知边的长度求解$OC$的长度。
【答案】：
解：
∵$\angle A=\angle C$，$\angle AOD=\angle COB$
∴$\bigtriangleup AOD\sim\bigtriangleup COB$
∴$\frac{OA}{OC}=\frac{OD}{OB}$
∵$OA = 6$，$OD = 8$，$OB = 4$
∴$\frac{6}{OC}=\frac{8}{4}$
$8OC=6×4$
$8OC=24$
$OC = 3$
故答案为$3$。

10. 如图,电灯$P在横杆AB$的正上方,$AB在灯光下的影子为CD$,$AB // CD$,$AB = 2m$,$CD = 5m$,点$P到CD的距离为3m$,则点$P到AB$的距离为______$m$。

$\frac{6}{5}$

答案： 解：设点P到AB的距离为$x$米。
∵ $AB // CD$，
∴ $\triangle PAB \sim \triangle PCD$。
∵ 相似三角形对应高的比等于相似比，
∴ $\frac{AB}{CD} = \frac{x}{3}$，即$\frac{2}{5} = \frac{x}{3}$。
解得$x = \frac{6}{5}$。
$\frac{6}{5}$