《2025年中学生世界九年级数学上册沪教版五四制》

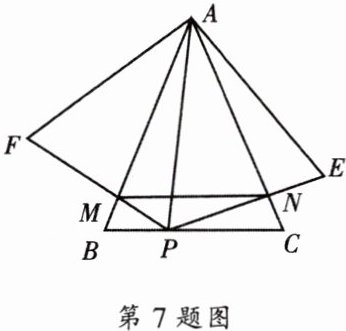
7. 如图,已知P是等腰三角形ABC的底边BC上的点,以AP为腰在AP的两侧分别作等腰三角形AFP和等腰三角形AEP,且$∠APF= ∠APE= ∠B$,$PF$交AB于点M,$PE$交AC于点N,联结MN.
求证:$MN// BC$.

答案： 证明：
∵△ABC是等腰三角形，
∴∠B=∠C。
∵∠APF=∠B，∠AMP=∠BMP，
∴△AMP∽△PMB（AA），
∴$\frac{AM}{PM}=\frac{PM}{BM}=\frac{AP}{BP}$，即$PM^2=AM\cdot BM$，$\frac{AM}{BM}=\frac{AP^2}{BP^2}$。
同理，∠APE=∠C，∠ANP=∠CNP，
∴△ANP∽△PNC（AA），
∴$\frac{AN}{PN}=\frac{PN}{CN}=\frac{AP}{CP}$，即$PN^2=AN\cdot CN$，$\frac{AN}{CN}=\frac{AP^2}{CP^2}$。
∵△ABC是等腰三角形，AB=AC，
又由△AMP∽△PMB和△ANP∽△PNC，可得$\frac{AM}{BM}=\frac{AN}{CN}$。
∴$\frac{AM}{AB-AM}=\frac{AN}{AC-AN}$，
∵AB=AC，
∴AM=AN，即$\frac{AM}{BM}=\frac{AN}{CN}$。
∴MN//BC（平行线分线段成比例逆定理）。
结论：MN//BC。

8. 如图,在$□ ABCD$中,已知$AE⊥BC$,$AF⊥CD$,垂足分别为E、F,联结EF.
求证:(1)$AB\cdot AF= AE\cdot AD$;
(2)$AC\cdot AF= BC\cdot EF$.

答案：
(1)证明：
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，∠B=∠D。
∵AE⊥BC，AF⊥CD，
∴∠AEB=∠AFD=90°。
∴△ABE∽△ADF。
∴$\frac{AB}{AD}=\frac{AE}{AF}$。
∴AB·AF=AE·AD。
(2)证明：
∵四边形ABCD是平行四边形，
∴∠B+∠C=180°。
∵AE⊥BC，AF⊥CD，
∴∠AEC=∠AFC=90°。
∴∠EAF+∠C=180°。
∴∠EAF=∠B。
由
(1)得$\frac{AE}{AB}=\frac{AF}{AD}$，且AD=BC，
∴$\frac{AE}{AB}=\frac{AF}{BC}$。
∴△AEF∽△BAC。
∴$\frac{AF}{BC}=\frac{EF}{AC}$。
∴AC·AF=BC·EF。

9. 如图,在$□ ABCD$中,已知点E、F分别在边AD、AB上,$∠ECB= ∠FCD$,$CE$、BA的延长线相交于点G.
求证:(1)$BC^{2}= BF\cdot BG$;
(2)$BF\cdot BA= DE\cdot AD$.

答案： 【解析】：
(1) 本题可通过证明三角形相似，利用相似三角形的性质来证明$BC^{2}= BF\cdot BG$。
首先，在平行四边形$ABCD$中，$AD// BC$，$AB// CD$，根据平行线的性质可得相关角相等。
因为$AB// CD$，所以$\angle FBC = \angle DCB$（两直线平行，内错角相等）；又因为$\angle ECB = \angle FCD$，所以$\angle FBC - \angle FCB = \angle DCB - \angle FCD$，即$\angle BFC = \angle BCG$。
再看$\triangle BFC$和$\triangle BCG$，它们有一个公共角$\angle B$，且$\angle BFC = \angle BCG$，根据两角分别相等的两个三角形相似，可得$\triangle BFC\sim\triangle BCG$。
由相似三角形的性质可知，对应边成比例，即$\frac{BF}{BC}=\frac{BC}{BG}$，交叉相乘就可得到$BC^{2}= BF\cdot BG$。
(2) 要证明$BF\cdot BA = DE\cdot AD$，可通过证明三角形相似，得到对应边成比例的关系，再结合平行四边形的性质进行推导。
因为$AD// BC$，所以$\angle DEC = \angle ECB$（两直线平行，内错角相等），又因为$\angle ECB = \angle FCD$，所以$\angle DEC = \angle FCD$。
再看$\triangle FBC$和$\triangle EDC$，$\angle FBC = \angle EDC$（$AB// CD$，同位角相等），$\angle BFC = \angle DEC$（已证），根据两角分别相等的两个三角形相似，可得$\triangle FBC\sim\triangle EDC$。
由相似三角形的性质可知，$\frac{BF}{DE}=\frac{BC}{DC}$。
因为四边形$ABCD$是平行四边形，所以$BC = AD$，$DC = BA$，将$BC = AD$，$DC = BA$代入$\frac{BF}{DE}=\frac{BC}{DC}$中，可得$\frac{BF}{DE}=\frac{AD}{BA}$，交叉相乘就得到$BF\cdot BA = DE\cdot AD$。
【答案】：
证明：
(1)
∵四边形$ABCD$是平行四边形，
∴$AD// BC$，$AB// CD$，
∴$\angle FBC = \angle DCB$，
∵$\angle ECB = \angle FCD$，
∴$\angle FBC - \angle FCB = \angle DCB - \angle FCD$，
即$\angle BFC = \angle BCG$，
又
∵$\angle B = \angle B$，
∴$\triangle BFC\sim\triangle BCG$，
∴$\frac{BF}{BC}=\frac{BC}{BG}$，
∴$BC^{2}= BF\cdot BG$。
(2)
∵$AD// BC$，
∴$\angle DEC = \angle ECB$，
∵$\angle ECB = \angle FCD$，
∴$\angle DEC = \angle FCD$，
∵$\angle FBC = \angle EDC$，$\angle BFC = \angle DEC$，
∴$\triangle FBC\sim\triangle EDC$，
∴$\frac{BF}{DE}=\frac{BC}{DC}$，
∵四边形$ABCD$是平行四边形，
∴$BC = AD$，$DC = BA$，
∴$\frac{BF}{DE}=\frac{AD}{BA}$，
∴$BF\cdot BA = DE\cdot AD$。

思维与拓展7
如图,已知$∠ABC= ∠CDB= 90^{\circ },AC= a,BC= b$,问:当BD与a,b之间满足怎样的关系时,$△ABC与△CDB$相似?

答案： 解：在$Rt\triangle ABC$中，$∠ABC=90^{\circ}$，$AC=a$，$BC=b$，由勾股定理得$AB=\sqrt{AC^{2}-BC^{2}}=\sqrt{a^{2}-b^{2}}$。
$∠ABC=∠CDB=90^{\circ}$，分两种情况讨论：
情况一：当$\triangle ABC\sim\triangle CDB$时，$\frac{AB}{CD}=\frac{BC}{DB}=\frac{AC}{CB}$，即$\frac{BC}{DB}=\frac{AC}{CB}$，$\frac{b}{BD}=\frac{a}{b}$，解得$BD=\frac{b^{2}}{a}$。
情况二：当$\triangle ABC\sim\triangle BDC$时，$\frac{AB}{BD}=\frac{BC}{DC}=\frac{AC}{BC}$，即$\frac{AB}{BD}=\frac{AC}{BC}$，$\frac{\sqrt{a^{2}-b^{2}}}{BD}=\frac{a}{b}$，解得$BD=\frac{b\sqrt{a^{2}-b^{2}}}{a}$。
综上，当$BD=\frac{b^{2}}{a}$或$BD=\frac{b\sqrt{a^{2}-b^{2}}}{a}$时，$\triangle ABC$与$\triangle CDB$相似。