1. 对一个图形进行放缩时,下列说法正确的是 (
A.图形中线段的长度与角的大小都保持不变;
B.图形中线段的长度与角的大小都会改变;
C.图形中线段的长度保持不变、角的大小可以改变;
D.图形中线段的长度可以改变、角的大小保持不变.
D
)A.图形中线段的长度与角的大小都保持不变;
B.图形中线段的长度与角的大小都会改变;
C.图形中线段的长度保持不变、角的大小可以改变;
D.图形中线段的长度可以改变、角的大小保持不变.
答案:
【解析】:
本题考察的是图形放缩的性质。在图形放缩的过程中,图形的形状是保持不变的,这意味着图形中的角的大小是保持不变的。但是,图形的尺寸会发生变化,即图形中线段的长度会按照一定的比例进行放缩。
A选项:图形中线段的长度与角的大小都保持不变。这是不正确的,因为虽然角的大小保持不变,但线段的长度会改变。
B选项:图形中线段的长度与角的大小都会改变。这也是不正确的,因为角的大小在图形放缩过程中是保持不变的。
C选项:图形中线段的长度保持不变、角的大小可以改变。这是不正确的,因为线段长度会改变,而角的大小保持不变。
D选项:图形中线段的长度可以改变、角的大小保持不变。这是正确的。在图形放缩的过程中,线段的长度会改变,但角的大小保持不变。
【答案】:
D
本题考察的是图形放缩的性质。在图形放缩的过程中,图形的形状是保持不变的,这意味着图形中的角的大小是保持不变的。但是,图形的尺寸会发生变化,即图形中线段的长度会按照一定的比例进行放缩。
A选项:图形中线段的长度与角的大小都保持不变。这是不正确的,因为虽然角的大小保持不变,但线段的长度会改变。
B选项:图形中线段的长度与角的大小都会改变。这也是不正确的,因为角的大小在图形放缩过程中是保持不变的。
C选项:图形中线段的长度保持不变、角的大小可以改变。这是不正确的,因为线段长度会改变,而角的大小保持不变。
D选项:图形中线段的长度可以改变、角的大小保持不变。这是正确的。在图形放缩的过程中,线段的长度会改变,但角的大小保持不变。
【答案】:
D
2. 下列选项中,一定是相似图形的是 (
A.两个边长不等的菱形;
B.两个周长相同的等腰三角形;
C.两个面积相等的直角三角形;
D.两个周长不同的正方形.
D
)A.两个边长不等的菱形;
B.两个周长相同的等腰三角形;
C.两个面积相等的直角三角形;
D.两个周长不同的正方形.
答案:
【解析】:
本题考查相似图形的定义,即两个图形如果形状相同但大小不一定相等,则它们是相似图形。
A选项:两个边长不等的菱形,虽然形状相同,但角度可能不同,因此不一定是相似图形。
B选项:两个周长相同的等腰三角形,形状和角度都可能不同,因此不一定是相似图形。
C选项:两个面积相等的直角三角形,同样形状和角度可能不同,因此不一定是相似图形。
D选项:两个周长不同的正方形,由于正方形的所有边都相等,所有角都是$90^\circ$,因此它们一定是相似图形。
【答案】:
D
本题考查相似图形的定义,即两个图形如果形状相同但大小不一定相等,则它们是相似图形。
A选项:两个边长不等的菱形,虽然形状相同,但角度可能不同,因此不一定是相似图形。
B选项:两个周长相同的等腰三角形,形状和角度都可能不同,因此不一定是相似图形。
C选项:两个面积相等的直角三角形,同样形状和角度可能不同,因此不一定是相似图形。
D选项:两个周长不同的正方形,由于正方形的所有边都相等,所有角都是$90^\circ$,因此它们一定是相似图形。
【答案】:
D
3. 下列各组图形中,一定相似的是 (
A.两个矩形;
B.两个菱形;
C.两个等腰梯形;
D.两个等边三角形.
D
)A.两个矩形;
B.两个菱形;
C.两个等腰梯形;
D.两个等边三角形.
答案:
【解析】:
本题考查图形的相似性。相似图形的定义是两个图形的形状相同但大小不一定相同。对于选项中的各种图形,我们需要分析它们的性质来判断是否一定相似。
A选项:两个矩形。矩形的所有角都是$90^\circ$,但长宽比例不一定相同,因此不一定相似。
B选项:两个菱形。菱形的所有边都相等,但角度不一定相同,因此不一定相似。
C选项:两个等腰梯形。等腰梯形的上下底边和腰的长度比例不一定相同,角度也不一定相同,因此不一定相似。
D选项:两个等边三角形。等边三角形的所有边都相等,所有角都是$60^\circ$,因此形状完全相同,大小不一定相同,满足相似图形的定义。
【答案】:
D
本题考查图形的相似性。相似图形的定义是两个图形的形状相同但大小不一定相同。对于选项中的各种图形,我们需要分析它们的性质来判断是否一定相似。
A选项:两个矩形。矩形的所有角都是$90^\circ$,但长宽比例不一定相同,因此不一定相似。
B选项:两个菱形。菱形的所有边都相等,但角度不一定相同,因此不一定相似。
C选项:两个等腰梯形。等腰梯形的上下底边和腰的长度比例不一定相同,角度也不一定相同,因此不一定相似。
D选项:两个等边三角形。等边三角形的所有边都相等,所有角都是$60^\circ$,因此形状完全相同,大小不一定相同,满足相似图形的定义。
【答案】:
D
4. 在比例尺为 $ 1:50000 $ 的地图上,图上距离为 $ 4 \mathrm{cm} $,则实际距离为
2
$ \mathrm{km} $.
答案:
【解析】:
本题主要考察比例尺的应用。比例尺表示的是图上的距离与实际距离的比例关系。
给定的比例尺为 $1:50000$,表示图上 $1 \mathrm{cm}$ 对应实际的 $50000 \mathrm{cm}$。
题目中给出图上的距离为 $4 \mathrm{cm}$,我们需要计算实际的距离。
设实际距离为 $x \mathrm{cm}$,根据比例尺,我们可以建立以下比例关系:
$\frac{1}{50000} = \frac{4}{x}$,
解这个比例式,我们得到:
$x = 4 × 50000 = 200000 \mathrm{cm}$,
由于题目要求实际距离的单位为 $\mathrm{km}$,我们需要进行单位转换。
因为 $1 \mathrm{km} = 100000 \mathrm{cm}$,所以:
$x = \frac{200000}{100000} = 2 \mathrm{km}$。
【答案】:
$2$
本题主要考察比例尺的应用。比例尺表示的是图上的距离与实际距离的比例关系。
给定的比例尺为 $1:50000$,表示图上 $1 \mathrm{cm}$ 对应实际的 $50000 \mathrm{cm}$。
题目中给出图上的距离为 $4 \mathrm{cm}$,我们需要计算实际的距离。
设实际距离为 $x \mathrm{cm}$,根据比例尺,我们可以建立以下比例关系:
$\frac{1}{50000} = \frac{4}{x}$,
解这个比例式,我们得到:
$x = 4 × 50000 = 200000 \mathrm{cm}$,
由于题目要求实际距离的单位为 $\mathrm{km}$,我们需要进行单位转换。
因为 $1 \mathrm{km} = 100000 \mathrm{cm}$,所以:
$x = \frac{200000}{100000} = 2 \mathrm{km}$。
【答案】:
$2$
5. 如果两地相距 $ 300 \mathrm{km} $,那么在 $ 1:10000000 $ 的地图上,它们相距
3
$ \mathrm{cm} $.
答案:
【解析】:
本题主要考察比例尺的应用以及单位换算。
首先,我们需要将实际距离从千米转换为厘米,因为地图上的距离是以厘米为单位的。
然后,我们使用比例尺来计算地图上的距离。
具体步骤如下:
1. 将实际距离$300km$转换为厘米:
$300 \text{km} = 300 × 1000 × 100 \text{cm} = 30000000 \text{cm}$
这里我们将千米转换为米,然后再将米转换为厘米。
2. 使用比例尺$1:10000000$来计算地图上的距离:
$\text{地图上的距离} = \frac{30000000 \text{cm}}{10000000} = 3 \text{cm}$
【答案】:
$3$
本题主要考察比例尺的应用以及单位换算。
首先,我们需要将实际距离从千米转换为厘米,因为地图上的距离是以厘米为单位的。
然后,我们使用比例尺来计算地图上的距离。
具体步骤如下:
1. 将实际距离$300km$转换为厘米:
$300 \text{km} = 300 × 1000 × 100 \text{cm} = 30000000 \text{cm}$
这里我们将千米转换为米,然后再将米转换为厘米。
2. 使用比例尺$1:10000000$来计算地图上的距离:
$\text{地图上的距离} = \frac{30000000 \text{cm}}{10000000} = 3 \text{cm}$
【答案】:
$3$
6. 已知甲、乙两地之间的距离为 $ 10 \mathrm{km} $,画在一张地图上的距离为 $ 5 \mathrm{cm} $,那么在这张地图上距离为 $ 2 \mathrm{cm} $ 的 $ A $、$ B $ 两地的实际距离为
4
$ \mathrm{km} $.
答案:
【解析】:
本题主要考察比例运算。首先,需要将地图上的距离与实际距离之间的比例计算出来,然后利用这个比例来求解$A$、$B$两地的实际距离。
已知甲、乙两地在地图上的距离为$5cm$,实际距离为$10km$。
根据$1km = 100000cm$,所以$10km = 1000000cm$。
所以,地图上的距离与实际距离的比例为:
$\frac{5cm}{1000000cm} = \frac{1}{200000}$,
即地图上$1cm$代表实际的$200000cm$,也就是$2km$。
接下来,利用这个比例来计算$A$、$B$两地的实际距离。
已知$A$、$B$两地在地图上的距离为$2cm$,那么实际距离为:
$2cm × 200000 = 400000cm$,
再根据$1km = 100000cm$,所以$400000cm = 4km$。
【答案】:
$4$
本题主要考察比例运算。首先,需要将地图上的距离与实际距离之间的比例计算出来,然后利用这个比例来求解$A$、$B$两地的实际距离。
已知甲、乙两地在地图上的距离为$5cm$,实际距离为$10km$。
根据$1km = 100000cm$,所以$10km = 1000000cm$。
所以,地图上的距离与实际距离的比例为:
$\frac{5cm}{1000000cm} = \frac{1}{200000}$,
即地图上$1cm$代表实际的$200000cm$,也就是$2km$。
接下来,利用这个比例来计算$A$、$B$两地的实际距离。
已知$A$、$B$两地在地图上的距离为$2cm$,那么实际距离为:
$2cm × 200000 = 400000cm$,
再根据$1km = 100000cm$,所以$400000cm = 4km$。
【答案】:
$4$
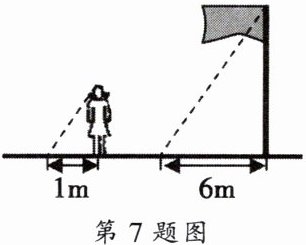
7. 如图,在同一时刻,测得小华和旗杆的影长分别为 $ 1 \mathrm{m} $ 和 $ 6 \mathrm{m} $,小华的身高约为 $ 1.6 \mathrm{m} $,则旗杆的高约为
9.6
$ \mathrm{m} $.
答案:
【解析】:本题考查的是利用相似三角形的性质来求解旗杆的高度。
在同一时刻,物体的高度和它的影长的比是相同的。
因此,小华的身高与影长的比应该等于旗杆的高度与其影长的比。
设旗杆的高度为 $h$ 米。
根据相似比例关系,可以得到以下等式:
$\frac{{\text{小华的身高}}}{{\text{小华的影长}}} = \frac{{\text{旗杆的高度}}}{{\text{旗杆的影长}}}$。
将已知数值代入等式,得到:
$\frac{1.6}{1} = \frac{h}{6}$。
通过交叉相乘,可以解出 $h$ 的值,即旗杆的高度。
【答案】:9.6。
在同一时刻,物体的高度和它的影长的比是相同的。
因此,小华的身高与影长的比应该等于旗杆的高度与其影长的比。
设旗杆的高度为 $h$ 米。
根据相似比例关系,可以得到以下等式:
$\frac{{\text{小华的身高}}}{{\text{小华的影长}}} = \frac{{\text{旗杆的高度}}}{{\text{旗杆的影长}}}$。
将已知数值代入等式,得到:
$\frac{1.6}{1} = \frac{h}{6}$。
通过交叉相乘,可以解出 $h$ 的值,即旗杆的高度。
【答案】:9.6。
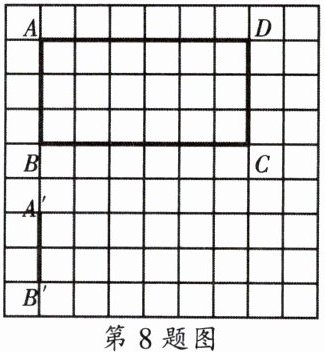
8. 如图,在方格图中画出与矩形 $ ABCD $ 相似的图形 $ A'B'C'D' $. (其中 $ AB $ 的对应边 $ A'B' $ 已在图中给出)

答案:
解:
1. 计算原矩形 $ABCD$ 的边长:设每个小方格边长为1,由图可知 $AB=2$,$BC=4$。
2. 确定相似比:已知 $A'B'=3$(对应 $AB$),相似比 $k=\frac{A'B'}{AB}=\frac{3}{2}$。
3. 计算对应边 $B'C'$:$B'C'=BC × k=4 × \frac{3}{2}=6$。
4. 画图:以 $A'B'$ 为边,向右作 $B'C'=6$,过 $A'$ 作 $A'D'=3$($AD=2$,$A'D'=AD × k=3$),连接 $D'C'$,得矩形 $A'B'C'D'$。
(注:因无法直接画图,实际作答需在方格图中按上述步骤画出图形。)
1. 计算原矩形 $ABCD$ 的边长:设每个小方格边长为1,由图可知 $AB=2$,$BC=4$。
2. 确定相似比:已知 $A'B'=3$(对应 $AB$),相似比 $k=\frac{A'B'}{AB}=\frac{3}{2}$。
3. 计算对应边 $B'C'$:$B'C'=BC × k=4 × \frac{3}{2}=6$。
4. 画图:以 $A'B'$ 为边,向右作 $B'C'=6$,过 $A'$ 作 $A'D'=3$($AD=2$,$A'D'=AD × k=3$),连接 $D'C'$,得矩形 $A'B'C'D'$。
(注:因无法直接画图,实际作答需在方格图中按上述步骤画出图形。)
查看更多完整答案,请扫码查看


