1. 下列命题正确的是 (
A.所有等腰三角形都相似;
B.两边成比例的两个等腰三角形相似;
C.有一个角相等的两个等腰三角形相似;
D.有一个角是$100^{\circ }$的两个等腰三角形相似.
D
)A.所有等腰三角形都相似;
B.两边成比例的两个等腰三角形相似;
C.有一个角相等的两个等腰三角形相似;
D.有一个角是$100^{\circ }$的两个等腰三角形相似.
答案:
解:A.等腰三角形的顶角和底角不一定对应相等,如顶角为30°的等腰三角形与顶角为40°的等腰三角形不相似,故A错误;
B.两边成比例,但夹角不一定相等,如一个等腰三角形的腰长为2,底边长为3,另一个等腰三角形的腰长为4,底边长为6,此时对应边成比例,但形状不同,不相似,故B错误;
C.相等的角可能一个是顶角,一个是底角,如等腰三角形ABC中∠A=30°(顶角),等腰三角形DEF中∠D=30°(底角),则两三角形不相似,故C错误;
D.100°的角只能是等腰三角形的顶角,所以两个等腰三角形的顶角都为100°,则底角都为(180°-100°)÷2=40°,三个角对应相等,所以相似,故D正确.
答案:D
B.两边成比例,但夹角不一定相等,如一个等腰三角形的腰长为2,底边长为3,另一个等腰三角形的腰长为4,底边长为6,此时对应边成比例,但形状不同,不相似,故B错误;
C.相等的角可能一个是顶角,一个是底角,如等腰三角形ABC中∠A=30°(顶角),等腰三角形DEF中∠D=30°(底角),则两三角形不相似,故C错误;
D.100°的角只能是等腰三角形的顶角,所以两个等腰三角形的顶角都为100°,则底角都为(180°-100°)÷2=40°,三个角对应相等,所以相似,故D正确.
答案:D
2. 如图,已知$∠AOD= 90^{\circ },OA= OB= BC= CD$,则下列结论正确的是 (
A.$△OAB\backsim △OCA;$
B.$△OAB\backsim △ODA;$
C.$△BAC\backsim △BDA;$
D.以上结论都不对.
C
)A.$△OAB\backsim △OCA;$
B.$△OAB\backsim △ODA;$
C.$△BAC\backsim △BDA;$
D.以上结论都不对.
答案:
解:设 $OA = OB = BC = CD = k$。
在 $Rt\triangle AOD$ 中,$OA = k$,$OD = 4k$,则 $AD = \sqrt{OA^2 + OD^2} = \sqrt{k^2 + (4k)^2} = \sqrt{17}k$。
$AB = \sqrt{OA^2 + OB^2} = \sqrt{k^2 + k^2} = \sqrt{2}k$,$AC = \sqrt{OA^2 + OC^2} = \sqrt{k^2 + (2k)^2} = \sqrt{5}k$,$BD = 2k$,$BC = k$。
选项A:$\triangle OAB$ 与 $\triangle OCA$。$\frac{OA}{OC} = \frac{k}{2k} = \frac{1}{2}$,$\frac{OB}{OA} = \frac{k}{k} = 1$,$\frac{AB}{CA} = \frac{\sqrt{2}k}{\sqrt{5}k} = \frac{\sqrt{10}}{5}$,三边不成比例,不相似。
选项B:$\triangle OAB$ 与 $\triangle ODA$。$\frac{OA}{OD} = \frac{k}{4k} = \frac{1}{4}$,$\frac{OB}{OA} = \frac{k}{k} = 1$,$\frac{AB}{DA} = \frac{\sqrt{2}k}{\sqrt{17}k} = \frac{\sqrt{34}}{17}$,三边不成比例,不相似。
选项C:$\triangle BAC$ 与 $\triangle BDA$。$\angle ABC = \angle DBA$(公共角)。$\frac{BC}{BA} = \frac{k}{\sqrt{2}k} = \frac{\sqrt{2}}{2}$,$\frac{BA}{BD} = \frac{\sqrt{2}k}{2k} = \frac{\sqrt{2}}{2}$,两边成比例且夹角相等,相似。
结论:选项C正确。
答案:C
在 $Rt\triangle AOD$ 中,$OA = k$,$OD = 4k$,则 $AD = \sqrt{OA^2 + OD^2} = \sqrt{k^2 + (4k)^2} = \sqrt{17}k$。
$AB = \sqrt{OA^2 + OB^2} = \sqrt{k^2 + k^2} = \sqrt{2}k$,$AC = \sqrt{OA^2 + OC^2} = \sqrt{k^2 + (2k)^2} = \sqrt{5}k$,$BD = 2k$,$BC = k$。
选项A:$\triangle OAB$ 与 $\triangle OCA$。$\frac{OA}{OC} = \frac{k}{2k} = \frac{1}{2}$,$\frac{OB}{OA} = \frac{k}{k} = 1$,$\frac{AB}{CA} = \frac{\sqrt{2}k}{\sqrt{5}k} = \frac{\sqrt{10}}{5}$,三边不成比例,不相似。
选项B:$\triangle OAB$ 与 $\triangle ODA$。$\frac{OA}{OD} = \frac{k}{4k} = \frac{1}{4}$,$\frac{OB}{OA} = \frac{k}{k} = 1$,$\frac{AB}{DA} = \frac{\sqrt{2}k}{\sqrt{17}k} = \frac{\sqrt{34}}{17}$,三边不成比例,不相似。
选项C:$\triangle BAC$ 与 $\triangle BDA$。$\angle ABC = \angle DBA$(公共角)。$\frac{BC}{BA} = \frac{k}{\sqrt{2}k} = \frac{\sqrt{2}}{2}$,$\frac{BA}{BD} = \frac{\sqrt{2}k}{2k} = \frac{\sqrt{2}}{2}$,两边成比例且夹角相等,相似。
结论:选项C正确。
答案:C
3. 在$△ABC和△A'B'C'$中,已知$∠B= ∠B'$,下列条件不能判断这两个三角形相似的是(
A.$∠A= ∠C';$
B.$∠A= ∠A';$
C.$\frac {AB}{BC}= \frac {A'B'}{B'C'};$
D.$\frac {AB}{AC}= \frac {A'B'}{A'C'}.$
D
)A.$∠A= ∠C';$
B.$∠A= ∠A';$
C.$\frac {AB}{BC}= \frac {A'B'}{B'C'};$
D.$\frac {AB}{AC}= \frac {A'B'}{A'C'}.$
答案:
解:A. 在$△ABC$和$△A'B'C'$中,$∠B=∠B'$,若$∠A=∠C'$,则$∠C=∠A'$,根据“两角分别相等的两个三角形相似”,可判断相似。
B. 若$∠A=∠A'$,且$∠B=∠B'$,根据“两角分别相等的两个三角形相似”,可判断相似。
C. 若$\frac{AB}{BC}=\frac{A'B'}{B'C'}$,且$∠B=∠B'$,根据“两边成比例且夹角相等的两个三角形相似”,可判断相似。
D. $\frac{AB}{AC}=\frac{A'B'}{A'C'}$,但$∠B$不是$AB$与$AC$的夹角,$∠B'$也不是$A'B'$与$A'C'$的夹角,不满足相似三角形的判定条件,不能判断相似。
答案:D
B. 若$∠A=∠A'$,且$∠B=∠B'$,根据“两角分别相等的两个三角形相似”,可判断相似。
C. 若$\frac{AB}{BC}=\frac{A'B'}{B'C'}$,且$∠B=∠B'$,根据“两边成比例且夹角相等的两个三角形相似”,可判断相似。
D. $\frac{AB}{AC}=\frac{A'B'}{A'C'}$,但$∠B$不是$AB$与$AC$的夹角,$∠B'$也不是$A'B'$与$A'C'$的夹角,不满足相似三角形的判定条件,不能判断相似。
答案:D
4. 如图,在$△ABC$中,已知DE不平行于BC,当$\frac {AB}{AE}= $

$\frac{AC}{AD}$
时,$△ABC\backsim △AED.$
答案:
【解析】:
题目考查相似三角形的判定定理2的内容,需要判断两个三角形相似的条件。
根据相似三角形的判定定理2,如果两个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似。
在题目中,已知$DE$不平行于$BC$,需要找到使得$\triangle ABC \sim \triangle AED$的条件。
观察图形,可以发现$\angle A$是$\triangle ABC$和$\triangle AED$的公共角,即$\angle BAC = \angle EAD$。
为了使$\triangle ABC \sim \triangle AED$,需要满足$\frac{AB}{AE} = \frac{AC}{AD}$。
由于题目只问了$\frac{AB}{AE}$的比值,而没有给出$AC$和$AD$的具体关系,但根据相似三角形的判定定理,可以知道当$\frac{AB}{AE} = \frac{AC}{AD}$时,两个三角形相似。
在这里,可以理解为当$\frac{AB}{AE}$等于某个常数时(即$\frac{AC}{AD}$的值),两个三角形就相似。
由于题目没有给出具体的边长,只能根据相似三角形的性质来填写答案。
根据相似三角形的判定定理2,可以得出当$\frac{AB}{AE} = \frac{AC}{AD}$时,$\triangle ABC \sim \triangle AED$。
由于题目只要求填写$\frac{AB}{AE}$的比值,可以简化为当$\frac{AB}{AE} = \frac{AC}{AD}$(或等价地,当两边对应成比例且夹角相等)时,两个三角形相似。
在这里,直接填写$\frac{AC}{AD}$作为答案,因为这是使得两个三角形相似的必要条件。
【答案】:
$\frac{AC}{AD}$。
题目考查相似三角形的判定定理2的内容,需要判断两个三角形相似的条件。
根据相似三角形的判定定理2,如果两个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似。
在题目中,已知$DE$不平行于$BC$,需要找到使得$\triangle ABC \sim \triangle AED$的条件。
观察图形,可以发现$\angle A$是$\triangle ABC$和$\triangle AED$的公共角,即$\angle BAC = \angle EAD$。
为了使$\triangle ABC \sim \triangle AED$,需要满足$\frac{AB}{AE} = \frac{AC}{AD}$。
由于题目只问了$\frac{AB}{AE}$的比值,而没有给出$AC$和$AD$的具体关系,但根据相似三角形的判定定理,可以知道当$\frac{AB}{AE} = \frac{AC}{AD}$时,两个三角形相似。
在这里,可以理解为当$\frac{AB}{AE}$等于某个常数时(即$\frac{AC}{AD}$的值),两个三角形就相似。
由于题目没有给出具体的边长,只能根据相似三角形的性质来填写答案。
根据相似三角形的判定定理2,可以得出当$\frac{AB}{AE} = \frac{AC}{AD}$时,$\triangle ABC \sim \triangle AED$。
由于题目只要求填写$\frac{AB}{AE}$的比值,可以简化为当$\frac{AB}{AE} = \frac{AC}{AD}$(或等价地,当两边对应成比例且夹角相等)时,两个三角形相似。
在这里,直接填写$\frac{AC}{AD}$作为答案,因为这是使得两个三角形相似的必要条件。
【答案】:
$\frac{AC}{AD}$。
5. 如上题,若$AB= 8,BC= 7,AE= 5$,则$DE= $
$\frac{35}{8}$
.
答案:
1. 首先,根据相似三角形的性质:
因为$\triangle ADE\sim\triangle ABC$(由上题可知),根据相似三角形对应边成比例,有$\frac{AD}{AB}=\frac{AE}{AC}$(相似三角形对应边成比例)。
设$DE = x$,由$\triangle ADE\sim\triangle ABC$可得$\frac{DE}{BC}=\frac{AE}{AC}$。
已知$AB = 8$,$BC = 7$,$AE = 5$,先求$AD$,$AD=AB - BD$,但这里我们直接用$\frac{DE}{BC}=\frac{AE}{AC}$(因为$\triangle ADE\sim\triangle ABC$),又因为$\frac{AD}{AB}=\frac{AE}{AC}$,$AD = AB - BD$,这里我们重新利用相似三角形对应边成比例$\frac{DE}{BC}=\frac{AE}{AB}$(因为$\triangle ADE\sim\triangle ABC$,对应边$DE$与$BC$,$AE$与$AB$)。
2. 然后,代入数值计算:
把$AB = 8$,$BC = 7$,$AE = 5$代入$\frac{DE}{BC}=\frac{AE}{AB}$中,得到$\frac{x}{7}=\frac{5}{8}$。
根据比例的性质“交叉相乘相等”,即$8x=5×7$。
则$x=\frac{35}{8}$。
所以$DE=\frac{35}{8}$。
因为$\triangle ADE\sim\triangle ABC$(由上题可知),根据相似三角形对应边成比例,有$\frac{AD}{AB}=\frac{AE}{AC}$(相似三角形对应边成比例)。
设$DE = x$,由$\triangle ADE\sim\triangle ABC$可得$\frac{DE}{BC}=\frac{AE}{AC}$。
已知$AB = 8$,$BC = 7$,$AE = 5$,先求$AD$,$AD=AB - BD$,但这里我们直接用$\frac{DE}{BC}=\frac{AE}{AC}$(因为$\triangle ADE\sim\triangle ABC$),又因为$\frac{AD}{AB}=\frac{AE}{AC}$,$AD = AB - BD$,这里我们重新利用相似三角形对应边成比例$\frac{DE}{BC}=\frac{AE}{AB}$(因为$\triangle ADE\sim\triangle ABC$,对应边$DE$与$BC$,$AE$与$AB$)。
2. 然后,代入数值计算:
把$AB = 8$,$BC = 7$,$AE = 5$代入$\frac{DE}{BC}=\frac{AE}{AB}$中,得到$\frac{x}{7}=\frac{5}{8}$。
根据比例的性质“交叉相乘相等”,即$8x=5×7$。
则$x=\frac{35}{8}$。
所以$DE=\frac{35}{8}$。
6. 在$△ABC和△A'B'C'$中,已知$∠B= ∠B',AB= 6,BC= 8,B'C'= 4$,则当$A'B'= $
3或$\frac{16}{3}$
时,$△ABC\backsim △A'B'C'.$
答案:
解:当△ABC∽△A'B'C'且∠B=∠B'时,根据相似三角形判定定理(两边对应成比例且夹角相等的两个三角形相似),有两种情况:
情况1:$\frac{AB}{A'B'}=\frac{BC}{B'C'}$
即$\frac{6}{A'B'}=\frac{8}{4}$
解得$A'B'=3$
情况2:$\frac{AB}{B'C'}=\frac{BC}{A'B'}$
即$\frac{6}{4}=\frac{8}{A'B'}$
解得$A'B'=\frac{16}{3}$
综上,$A'B'=3$或$\frac{16}{3}$
答案:3或$\frac{16}{3}$
情况1:$\frac{AB}{A'B'}=\frac{BC}{B'C'}$
即$\frac{6}{A'B'}=\frac{8}{4}$
解得$A'B'=3$
情况2:$\frac{AB}{B'C'}=\frac{BC}{A'B'}$
即$\frac{6}{4}=\frac{8}{A'B'}$
解得$A'B'=\frac{16}{3}$
综上,$A'B'=3$或$\frac{16}{3}$
答案:3或$\frac{16}{3}$
7. 如图,已知四边形ABCD的对角线AC与BD相交于点O,$∠ADO= ∠BCO.$
求证:$△ABO\backsim △DCO.$
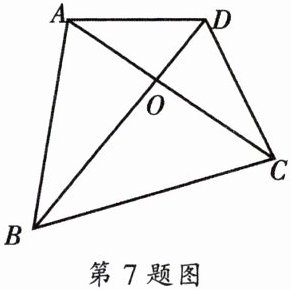
求证:$△ABO\backsim △DCO.$

答案:
证明:
∵∠ADO=∠BCO,∠AOD=∠BOC(对顶角相等),
∴△AOD∽△BOC(两角对应相等的两个三角形相似)。
∴AO/BO=DO/CO(相似三角形对应边成比例)。
∵∠AOB=∠DOC(对顶角相等),
∴△ABO∽△DCO(两边对应成比例且夹角相等的两个三角形相似)。
∵∠ADO=∠BCO,∠AOD=∠BOC(对顶角相等),
∴△AOD∽△BOC(两角对应相等的两个三角形相似)。
∴AO/BO=DO/CO(相似三角形对应边成比例)。
∵∠AOB=∠DOC(对顶角相等),
∴△ABO∽△DCO(两边对应成比例且夹角相等的两个三角形相似)。
查看更多完整答案,请扫码查看


