1. 如图,在$\triangle ABC$中,已知点$D$、$E$、$F分别是AB$、$AC$、$BC$的中点.设$\overrightarrow {BA}= \overrightarrow {a}$,$\overrightarrow {BC}= \overrightarrow {b}$,下列向量可以表示为$\frac {1}{2}\overrightarrow {b}-\overrightarrow {a}$的是 (

A.$\overrightarrow {AC}$;
B.$\overrightarrow {AF}$;
C.$\overrightarrow {BE}$;
D.$\overrightarrow {CD}$.
B
) 
A.$\overrightarrow {AC}$;
B.$\overrightarrow {AF}$;
C.$\overrightarrow {BE}$;
D.$\overrightarrow {CD}$.
答案:
解:
∵$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$,
∴$\overrightarrow{AC}=\overrightarrow{BC}-\overrightarrow{BA}=\overrightarrow{b}-\overrightarrow{a}$,
$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}=\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}$,
$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=\overrightarrow{a}+\frac{1}{2}\overrightarrow{AC}=\overrightarrow{a}+\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,
$\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BD}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{BA}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}=\frac{1}{2}\overrightarrow{a}-\overrightarrow{b}$。
答案:B
∵$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$,
∴$\overrightarrow{AC}=\overrightarrow{BC}-\overrightarrow{BA}=\overrightarrow{b}-\overrightarrow{a}$,
$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}=\frac{1}{2}\overrightarrow{b}-\overrightarrow{a}$,
$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=\overrightarrow{a}+\frac{1}{2}\overrightarrow{AC}=\overrightarrow{a}+\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,
$\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BD}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{BA}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}=\frac{1}{2}\overrightarrow{a}-\overrightarrow{b}$。
答案:B
2. 如果平行四边形$ABCD的对角线AC与BD交于点O$,$\overrightarrow {AB}= \overrightarrow {a}$,$\overrightarrow {BC}= \overrightarrow {b}$,那么$\overrightarrow {CO}$可以表示为 (
A.$\frac {1}{2}\overrightarrow {a}+\frac {1}{2}\overrightarrow {b}$;
B.$-\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$;
C.$\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$;
D.$\frac {1}{2}\overrightarrow {b}-\frac {1}{2}\overrightarrow {a}$.
B
)A.$\frac {1}{2}\overrightarrow {a}+\frac {1}{2}\overrightarrow {b}$;
B.$-\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$;
C.$\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$;
D.$\frac {1}{2}\overrightarrow {b}-\frac {1}{2}\overrightarrow {a}$.
答案:
【解析】:
首先,由平行四边形的性质,我们知道对角线互相平分,即点O是AC和BD的中点。
因此,向量$\overrightarrow{AO}$是向量$\overrightarrow{AC}$的一半,同理$\overrightarrow{CO}$也是$\overrightarrow{AC}$的一半但方向相反。
向量$\overrightarrow{AC}$可以由$\overrightarrow{AB}$和$\overrightarrow{BC}$的和得到,即$\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{a} + \overrightarrow{b}$。
由于O是AC的中点,所以$\overrightarrow{CO} = -\frac{1}{2} \overrightarrow{AC} = -\frac{1}{2}(\overrightarrow{a} + \overrightarrow{b}) = -\frac{1}{2}\overrightarrow{a} - \frac{1}{2}\overrightarrow{b}$。
【答案】:
B. $-\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$。
首先,由平行四边形的性质,我们知道对角线互相平分,即点O是AC和BD的中点。
因此,向量$\overrightarrow{AO}$是向量$\overrightarrow{AC}$的一半,同理$\overrightarrow{CO}$也是$\overrightarrow{AC}$的一半但方向相反。
向量$\overrightarrow{AC}$可以由$\overrightarrow{AB}$和$\overrightarrow{BC}$的和得到,即$\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{a} + \overrightarrow{b}$。
由于O是AC的中点,所以$\overrightarrow{CO} = -\frac{1}{2} \overrightarrow{AC} = -\frac{1}{2}(\overrightarrow{a} + \overrightarrow{b}) = -\frac{1}{2}\overrightarrow{a} - \frac{1}{2}\overrightarrow{b}$。
【答案】:
B. $-\frac {1}{2}\overrightarrow {a}-\frac {1}{2}\overrightarrow {b}$。
3. 如图,已知$\overrightarrow {OA}= 3\overrightarrow {a}$,$\overrightarrow {OB}= 3\overrightarrow {b}$,$C$、$D是线段AB$的两个三等分点,则$\overrightarrow {CD}$等于 (
A.$\overrightarrow {a}-\overrightarrow {b}$;
B.$\overrightarrow {b}-\overrightarrow {a}$;
C.$\overrightarrow {a}+\overrightarrow {b}$;
D.$-\overrightarrow {a}-\overrightarrow {b}$.
B
)A.$\overrightarrow {a}-\overrightarrow {b}$;
B.$\overrightarrow {b}-\overrightarrow {a}$;
C.$\overrightarrow {a}+\overrightarrow {b}$;
D.$-\overrightarrow {a}-\overrightarrow {b}$.
答案:
【解析】:本题可根据向量的加减法运算法则,结合$C$、$D$是线段$AB$的两个三等分点这一条件,求出$\overrightarrow{CD}$。
步骤一:用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AB}$
已知$\overrightarrow{OA}= 3\overrightarrow{a}$,$\overrightarrow{OB}= 3\overrightarrow{b}$,根据向量减法的三角形法则:$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,将$\overrightarrow{OA}= 3\overrightarrow{a}$,$\overrightarrow{OB}= 3\overrightarrow{b}$代入可得:
$\overrightarrow{AB}=3\overrightarrow{b}-3\overrightarrow{a}$
步骤二:用$\overrightarrow{AB}$表示$\overrightarrow{CD}$
因为$C$、$D$是线段$AB$的两个三等分点,所以$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{AB}$。
将$\overrightarrow{AB}=3\overrightarrow{b}-3\overrightarrow{a}$代入$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{AB}$可得:
$\overrightarrow{CD}=\frac{1}{3}(3\overrightarrow{b}-3\overrightarrow{a})=\overrightarrow{b}-\overrightarrow{a}$
【答案】:B
步骤一:用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AB}$
已知$\overrightarrow{OA}= 3\overrightarrow{a}$,$\overrightarrow{OB}= 3\overrightarrow{b}$,根据向量减法的三角形法则:$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,将$\overrightarrow{OA}= 3\overrightarrow{a}$,$\overrightarrow{OB}= 3\overrightarrow{b}$代入可得:
$\overrightarrow{AB}=3\overrightarrow{b}-3\overrightarrow{a}$
步骤二:用$\overrightarrow{AB}$表示$\overrightarrow{CD}$
因为$C$、$D$是线段$AB$的两个三等分点,所以$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{AB}$。
将$\overrightarrow{AB}=3\overrightarrow{b}-3\overrightarrow{a}$代入$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{AB}$可得:
$\overrightarrow{CD}=\frac{1}{3}(3\overrightarrow{b}-3\overrightarrow{a})=\overrightarrow{b}-\overrightarrow{a}$
【答案】:B
4. 已知$\overrightarrow {a}$、$\overrightarrow {b}$是两个不平行的向量,$\overrightarrow {c}= \frac {1}{2}\overrightarrow {a}-\overrightarrow {b}$,则向量$\overrightarrow {c}在\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量分别是
$\frac{1}{2}\overrightarrow{a}$,$-\overrightarrow{b}$
.
答案:
【解析】:
本题考查平面向量的基本定理及其意义,这个定理表明,如果$\overrightarrow {a}$、$\overrightarrow {b}$是同一平面内的两个不共线向量,那么对于该平面内的任一向量$\overrightarrow {c}$,有且只有一对实数$\lambda$、$\mu$,使$\overrightarrow {c}=\lambda \overrightarrow {a}+\mu \overrightarrow {b}$,其中把不共线的向量$\overrightarrow {a}$、$\overrightarrow {b}$叫做表示这一平面内所有向量的一组基底。记$\overrightarrow {c}= \lambda \overrightarrow {a}+\mu \overrightarrow {b}$,则$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量分别是$\lambda \overrightarrow {a}$和$\mu \overrightarrow {b}$。本题根据平面向量的基本定理,结合已知条件,即可得出答案。
根据平面向量的基本定理,如果$\overrightarrow {a}$、$\overrightarrow {b}$是同一平面内的两个不共线向量,
那么对于该平面内的任一向量$\overrightarrow {c}$,存在唯一的一对实数$\lambda$、$\mu$,
使得$\overrightarrow {c}=\lambda \overrightarrow {a}+\mu \overrightarrow {b}$,
其中$\lambda \overrightarrow {a}$和$\mu \overrightarrow {b}$分别是向量$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量。
题目给出了$\overrightarrow {c}= \frac {1}{2}\overrightarrow {a}-\overrightarrow {b}$,
对比平面向量的基本定理,我们可以得出:
$\lambda = \frac{1}{2}$,$\mu = -1$,
因此,向量$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量分别是$\frac{1}{2}\overrightarrow {a}$和$- \overrightarrow {b}$。
【答案】:
$\frac{1}{2}\overrightarrow {a}$,$- \overrightarrow {b}$
本题考查平面向量的基本定理及其意义,这个定理表明,如果$\overrightarrow {a}$、$\overrightarrow {b}$是同一平面内的两个不共线向量,那么对于该平面内的任一向量$\overrightarrow {c}$,有且只有一对实数$\lambda$、$\mu$,使$\overrightarrow {c}=\lambda \overrightarrow {a}+\mu \overrightarrow {b}$,其中把不共线的向量$\overrightarrow {a}$、$\overrightarrow {b}$叫做表示这一平面内所有向量的一组基底。记$\overrightarrow {c}= \lambda \overrightarrow {a}+\mu \overrightarrow {b}$,则$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量分别是$\lambda \overrightarrow {a}$和$\mu \overrightarrow {b}$。本题根据平面向量的基本定理,结合已知条件,即可得出答案。
根据平面向量的基本定理,如果$\overrightarrow {a}$、$\overrightarrow {b}$是同一平面内的两个不共线向量,
那么对于该平面内的任一向量$\overrightarrow {c}$,存在唯一的一对实数$\lambda$、$\mu$,
使得$\overrightarrow {c}=\lambda \overrightarrow {a}+\mu \overrightarrow {b}$,
其中$\lambda \overrightarrow {a}$和$\mu \overrightarrow {b}$分别是向量$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量。
题目给出了$\overrightarrow {c}= \frac {1}{2}\overrightarrow {a}-\overrightarrow {b}$,
对比平面向量的基本定理,我们可以得出:
$\lambda = \frac{1}{2}$,$\mu = -1$,
因此,向量$\overrightarrow {c}$在$\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量分别是$\frac{1}{2}\overrightarrow {a}$和$- \overrightarrow {b}$。
【答案】:
$\frac{1}{2}\overrightarrow {a}$,$- \overrightarrow {b}$
5. 已知在平行四边形$ABCD$中,点$M$、$N分别是边DC$、$BC$的中点,$\overrightarrow {AB}= \overrightarrow {a}$,$\overrightarrow {AD}= \overrightarrow {b}$,那么$MN关于\overrightarrow {a}$、$\overrightarrow {b}$的分解式是______
$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$
.
答案:
解:在平行四边形$ABCD$中,$\overrightarrow{DC}=\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{b}$。
因为点$M$是边$DC$的中点,所以$\overrightarrow{MC}=\frac{1}{2}\overrightarrow{DC}=\frac{1}{2}\overrightarrow{a}$。
因为点$N$是边$BC$的中点,所以$\overrightarrow{NC}=-\frac{1}{2}\overrightarrow{BC}=-\frac{1}{2}\overrightarrow{b}$。
则$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\overrightarrow{MC}-\overrightarrow{NC}=\frac{1}{2}\overrightarrow{a}-\left(-\frac{1}{2}\overrightarrow{b}\right)=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$。
$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$
因为点$M$是边$DC$的中点,所以$\overrightarrow{MC}=\frac{1}{2}\overrightarrow{DC}=\frac{1}{2}\overrightarrow{a}$。
因为点$N$是边$BC$的中点,所以$\overrightarrow{NC}=-\frac{1}{2}\overrightarrow{BC}=-\frac{1}{2}\overrightarrow{b}$。
则$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\overrightarrow{MC}-\overrightarrow{NC}=\frac{1}{2}\overrightarrow{a}-\left(-\frac{1}{2}\overrightarrow{b}\right)=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$。
$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$
6. 如果点$O是\triangle ABC$的重心,则$\overrightarrow {OA}+\overrightarrow {OB}+\overrightarrow {OC}= $
$\vec{0}$
.
答案:
解:因为点$O$是$\triangle ABC$的重心,延长$AO$交$BC$于点$D$,则$D$为$BC$中点,且$AO = \frac{2}{3}AD$。
$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AB} + \frac{1}{2}\overrightarrow{BC} = \overrightarrow{AB} + \frac{1}{2}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$
$\overrightarrow{AO} = \frac{2}{3}\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$
$\overrightarrow{OA} = -\overrightarrow{AO} = -\frac{1}{3}\overrightarrow{AB} - \frac{1}{3}\overrightarrow{AC}$
同理,延长$BO$交$AC$于点$E$,$E$为$AC$中点,$\overrightarrow{OB} = -\frac{1}{3}\overrightarrow{BA} - \frac{1}{3}\overrightarrow{BC}$
延长$CO$交$AB$于点$F$,$F$为$AB$中点,$\overrightarrow{OC} = -\frac{1}{3}\overrightarrow{CA} - \frac{1}{3}\overrightarrow{CB}$
$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = -\frac{1}{3}(\overrightarrow{AB} + \overrightarrow{BA} + \overrightarrow{AC} + \overrightarrow{CA} + \overrightarrow{BC} + \overrightarrow{CB}) = -\frac{1}{3}(\vec{0} + \vec{0} + \vec{0}) = \vec{0}$
$\vec{0}$
$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AB} + \frac{1}{2}\overrightarrow{BC} = \overrightarrow{AB} + \frac{1}{2}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$
$\overrightarrow{AO} = \frac{2}{3}\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$
$\overrightarrow{OA} = -\overrightarrow{AO} = -\frac{1}{3}\overrightarrow{AB} - \frac{1}{3}\overrightarrow{AC}$
同理,延长$BO$交$AC$于点$E$,$E$为$AC$中点,$\overrightarrow{OB} = -\frac{1}{3}\overrightarrow{BA} - \frac{1}{3}\overrightarrow{BC}$
延长$CO$交$AB$于点$F$,$F$为$AB$中点,$\overrightarrow{OC} = -\frac{1}{3}\overrightarrow{CA} - \frac{1}{3}\overrightarrow{CB}$
$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = -\frac{1}{3}(\overrightarrow{AB} + \overrightarrow{BA} + \overrightarrow{AC} + \overrightarrow{CA} + \overrightarrow{BC} + \overrightarrow{CB}) = -\frac{1}{3}(\vec{0} + \vec{0} + \vec{0}) = \vec{0}$
$\vec{0}$
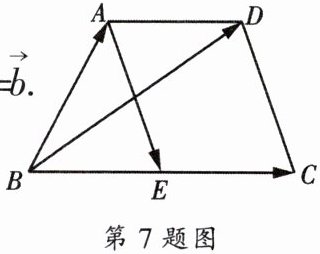
7. 如图,在梯形$ABCD$中,$AD// BC$,$BC= 2AD$,$E是BC$的中点.已知$\overrightarrow {BC}= \overrightarrow {a}$,$\overrightarrow {BA}= \overrightarrow {b}$.
(1)请使用$\overrightarrow {a}$、$\overrightarrow {b}的线性组合表示向量\overrightarrow {BD}$、$\overrightarrow {AE}$;
(2)画出$\overrightarrow {BD}分别在\overrightarrow {BC}$、$\overrightarrow {BA}$方向上的分向量.(不写画法,保留画图痕迹)
(1)请使用$\overrightarrow {a}$、$\overrightarrow {b}的线性组合表示向量\overrightarrow {BD}$、$\overrightarrow {AE}$;
(2)画出$\overrightarrow {BD}分别在\overrightarrow {BC}$、$\overrightarrow {BA}$方向上的分向量.(不写画法,保留画图痕迹)

答案:
【解析】:
本题主要考查平面向量的线性运算以及向量在特定方向上的分解,涉及到梯形的性质、向量的加减法等知识点。
(1)求$\overrightarrow{BD}$和$\overrightarrow{AE}$:
对于$\overrightarrow{BD}$,根据向量加法的三角形法则,$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}$。
已知$AD// BC$,$BC = 2AD$,$E$是$BC$的中点,所以$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{BC}$,又因为$\overrightarrow{BC}=\overrightarrow{a}$,$\overrightarrow{BA}=\overrightarrow{b}$,则$\overrightarrow{BD}=\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}$。
对于$\overrightarrow{AE}$,因为$E$是$BC$中点,$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}\overrightarrow{a}$,根据向量加法的三角形法则$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}$,而$\overrightarrow{AB}=-\overrightarrow{BA}=-\overrightarrow{b}$,所以$\overrightarrow{AE}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}$。
(2)画$\overrightarrow{BD}$分别在$\overrightarrow{BC}$、$\overrightarrow{BA}$方向上的分向量:
过点$D$作$DM// BA$交$BC$于点$M$,过点$D$作$DN// BC$交$BA$的延长线于点$N$。
则$\overrightarrow{DM}$就是$\overrightarrow{BD}$在$\overrightarrow{BC}$方向上的分向量,$\overrightarrow{BN}$就是$\overrightarrow{BD}$在$\overrightarrow{BA}$方向上的分向量。
【答案】:
(1)$\overrightarrow {BD}=\overrightarrow {b}+\frac {1}{2}\overrightarrow {a}$,$\overrightarrow {AE}=\frac {1}{2}\overrightarrow {a}-\overrightarrow {b}$。
(2)图略。
本题主要考查平面向量的线性运算以及向量在特定方向上的分解,涉及到梯形的性质、向量的加减法等知识点。
(1)求$\overrightarrow{BD}$和$\overrightarrow{AE}$:
对于$\overrightarrow{BD}$,根据向量加法的三角形法则,$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}$。
已知$AD// BC$,$BC = 2AD$,$E$是$BC$的中点,所以$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{BC}$,又因为$\overrightarrow{BC}=\overrightarrow{a}$,$\overrightarrow{BA}=\overrightarrow{b}$,则$\overrightarrow{BD}=\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}$。
对于$\overrightarrow{AE}$,因为$E$是$BC$中点,$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}\overrightarrow{a}$,根据向量加法的三角形法则$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}$,而$\overrightarrow{AB}=-\overrightarrow{BA}=-\overrightarrow{b}$,所以$\overrightarrow{AE}=-\overrightarrow{b}+\frac{1}{2}\overrightarrow{a}$。
(2)画$\overrightarrow{BD}$分别在$\overrightarrow{BC}$、$\overrightarrow{BA}$方向上的分向量:
过点$D$作$DM// BA$交$BC$于点$M$,过点$D$作$DN// BC$交$BA$的延长线于点$N$。
则$\overrightarrow{DM}$就是$\overrightarrow{BD}$在$\overrightarrow{BC}$方向上的分向量,$\overrightarrow{BN}$就是$\overrightarrow{BD}$在$\overrightarrow{BA}$方向上的分向量。
【答案】:
(1)$\overrightarrow {BD}=\overrightarrow {b}+\frac {1}{2}\overrightarrow {a}$,$\overrightarrow {AE}=\frac {1}{2}\overrightarrow {a}-\overrightarrow {b}$。
(2)图略。
查看更多完整答案,请扫码查看


