《2025年中学生世界九年级数学上册沪教版五四制》

9. 如果$k = 0或\overrightarrow a = \overrightarrow 0$,那么$k\overrightarrow a = $$\overrightarrow 0$.

答案： 【解析】：
本题考查实数与向量相乘的性质。根据实数与向量相乘的定义，当实数为0或向量为零向量时，它们的乘积为零向量。
【答案】：
$\overrightarrow 0$

10. 已知非零向量$\overrightarrow {OA} = \overrightarrow a$,向量$\overrightarrow {OB}与\overrightarrow a$的方向相同,它的长度是$\left| {\overrightarrow a } \right|$的6倍,则$\overrightarrow {OB} = $$6\overrightarrow{a}$.

答案： 【解析】：
本题考查了向量的数乘性质，特别是当数乘因子为正数时，向量的方向与原向量相同，长度则按数乘因子的绝对值进行伸缩。
已知非零向量$\overrightarrow{OA} = \overrightarrow{a}$，向量$\overrightarrow{OB}$与$\overrightarrow{a}$的方向相同，且其长度是$\left|\overrightarrow{a}\right|$的6倍。
根据向量的数乘定义，当数乘因子为正数时，新向量的方向与原向量相同，长度则变为原向量长度的数乘因子倍。
因此，可以得到$\overrightarrow{OB} = 6\overrightarrow{a}$。
【答案】：
$\overrightarrow{OB} = 6\overrightarrow{a}$

11. 如果非零向量$\overrightarrow a与\overrightarrow b满足等式\overrightarrow a = - 3\overrightarrow b$,那么向量$\overrightarrow a与\overrightarrow b$的方向相反.

答案： 【解析】：
本题考查向量的数乘性质。根据向量数乘的定义，当向量乘以一个正数时，向量的方向不变；当向量乘以一个负数时，向量的方向与原方向相反。由题意，有$\overrightarrow a = - 3\overrightarrow b$，即$\overrightarrow a$是$\overrightarrow b$的-3倍，所以$\overrightarrow a$与$\overrightarrow b$的方向相反。
【答案】：
相反

12. 已知向量$\overrightarrow a与向量\overrightarrow b$的方向相反,且$\left| {\overrightarrow a } \right| = 3\left| {\overrightarrow b } \right|$,则$\overrightarrow a = $-3$\overrightarrow b$.

答案： 【解析】：
题目考查了实数与向量相乘的性质，特别是当两个向量方向相反且模长有特定关系时，如何用一个向量表示另一个向量。
由于向量$\overrightarrow a$与向量$\overrightarrow b$的方向相反，且$|\overrightarrow a| = 3|\overrightarrow b|$，根据实数与向量相乘的定义，当一个向量的模是另一个向量模的k倍，且方向相反时，可以用$-k$倍的另一个向量来表示这个向量。
因此，有$\overrightarrow a = -3\overrightarrow b$。
【答案】：
$\overrightarrow a = -3\overrightarrow b$。

13. 已知在梯形ABCD中,$AD// BC$,点E在AB上,点F在CD上,EF是中位线.若$\overrightarrow {AD} = \overrightarrow a$,$\overrightarrow {EF} = \overrightarrow b$,则用$\overrightarrow a$、$\overrightarrow b表示\overrightarrow {BC} = $$2\overrightarrow{b} - \overrightarrow{a}$.

答案： 【解析】：
本题主要考查了平面向量的线性运算及梯形中位线的性质。
首先，由梯形的性质，我们知道梯形的中位线长度是上下底之和的一半，即：
$EF = \frac{AD + BC}{2}$，
给定$EF$是中位线，且已知向量$\overrightarrow{AD} = \overrightarrow{a}$ 和 $\overrightarrow{EF} = \overrightarrow{b}$。
我们可以将上述梯形中位线的性质转化为向量形式：
$\overrightarrow{EF} = \frac{\overrightarrow{AD} + \overrightarrow{BC}}{2}$，
代入已知的向量值，我们得到：
$\overrightarrow{b} = \frac{\overrightarrow{a} + \overrightarrow{BC}}{2}$，
解这个方程，我们可以找到$\overrightarrow{BC}$的表达式：
$\overrightarrow{BC} = 2\overrightarrow{b} - \overrightarrow{a}$。
【答案】：
$\overrightarrow{BC} = 2\overrightarrow{b} - \overrightarrow{a}$。

14. 已知非零向量$\overrightarrow a$,求作:向量$\frac{3}{4}\overrightarrow a$.

答案： 解：1. 作射线 $ OP $；
2. 在射线 $ OP $ 上取点 $ A $，使 $ \overrightarrow{OA} = \overrightarrow{a} $；
3. 将线段 $ OA $ 四等分，取靠近点 $ O $ 的前三等份，记终点为 $ B $；
4. 则向量 $ \overrightarrow{OB} $ 即为所求作的向量 $ \frac{3}{4}\overrightarrow{a} $。

15. 如图,矩形ABCD中,已知点E、M和F、N分别是AB、DC的三等分点.设$\overrightarrow {AB} = \overrightarrow a$,$\overrightarrow {DA} = \overrightarrow b$,试用向量$\overrightarrow a$、$\overrightarrow b表示向量\overrightarrow {AE}$、$\overrightarrow {AD}$,并写出图中与$\overrightarrow {AE}$、$\overrightarrow {AD}$相等的向量.

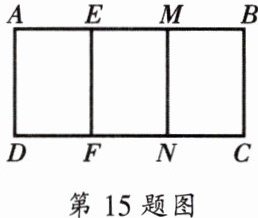
答案： 解：
$\overrightarrow{AE} = \frac{1}{3}\overrightarrow{a}$，
$\overrightarrow{AD} = -\overrightarrow{b}$。
与$\overrightarrow{AE}$相等的向量：$\overrightarrow{EM}$、$\overrightarrow{MB}$、$\overrightarrow{DF}$、$\overrightarrow{FN}$、$\overrightarrow{NC}$；
与$\overrightarrow{AD}$相等的向量：$\overrightarrow{BC}$、$\overrightarrow{EF}$、$\overrightarrow{MN}$。