11. 在直角坐标平面内有一点$P(2,4)$,求$OP与x轴正半轴的夹角α$的四个三角比的值.
答案:
【解析】:
本题主要考察直角坐标系中任意角的三角比的定义。在直角坐标系中,对于任意角$α$,其正弦值为对边长度除以斜边长度,余弦值为邻边长度除以斜边长度,正切值为对边长度除以邻边长度。题目给出了点$P(2,4)$,因此我们可以计算出$OP$的长度,即斜边长度,然后利用三角比的定义求出$α$的正弦、余弦、正切值。
首先,我们需要计算点$P$到原点$O$的距离,即斜边$OP$的长度。根据勾股定理,$OP = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5}$。
然后,我们可以利用三角比的定义来求解。
* 正弦值:$\sinα = \frac{对边}{斜边} = \frac{4}{2\sqrt{5}} = \frac{2\sqrt{5}}{5}$。
* 余弦值:$\cosα = \frac{邻边}{斜边} = \frac{2}{2\sqrt{5}} = \frac{\sqrt{5}}{5}$。
* 正切值:$\tanα = \frac{对边}{邻边} = \frac{4}{2} = 2$。
* 余切值为正切的倒数:$\cotα = \frac{1}{\tanα} = \frac{1}{2}$。
【答案】:
解:
$\sinα = \frac{2\sqrt{5}}{5}$;
$\cosα = \frac{\sqrt{5}}{5}$;
$\tanα = 2$;
$\cotα = \frac{1}{2}$。
本题主要考察直角坐标系中任意角的三角比的定义。在直角坐标系中,对于任意角$α$,其正弦值为对边长度除以斜边长度,余弦值为邻边长度除以斜边长度,正切值为对边长度除以邻边长度。题目给出了点$P(2,4)$,因此我们可以计算出$OP$的长度,即斜边长度,然后利用三角比的定义求出$α$的正弦、余弦、正切值。
首先,我们需要计算点$P$到原点$O$的距离,即斜边$OP$的长度。根据勾股定理,$OP = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5}$。
然后,我们可以利用三角比的定义来求解。
* 正弦值:$\sinα = \frac{对边}{斜边} = \frac{4}{2\sqrt{5}} = \frac{2\sqrt{5}}{5}$。
* 余弦值:$\cosα = \frac{邻边}{斜边} = \frac{2}{2\sqrt{5}} = \frac{\sqrt{5}}{5}$。
* 正切值:$\tanα = \frac{对边}{邻边} = \frac{4}{2} = 2$。
* 余切值为正切的倒数:$\cotα = \frac{1}{\tanα} = \frac{1}{2}$。
【答案】:
解:
$\sinα = \frac{2\sqrt{5}}{5}$;
$\cosα = \frac{\sqrt{5}}{5}$;
$\tanα = 2$;
$\cotα = \frac{1}{2}$。
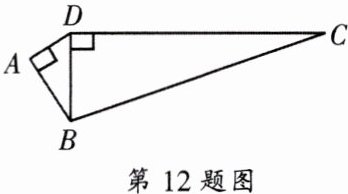
12. 如图,在四边形$ABCD$中,已知$∠BAD = ∠BDC = 90^{\circ}$,且$AD = 3$,$sin∠ABD= \frac{3}{5}$,$sin∠DBC= \frac{12}{13}$,求$AB$、$BC$、$CD$的长.

答案:
解:在Rt△ABD中,∠BAD=90°,AD=3,sin∠ABD=AD/BD=3/5,
设AD=3k,BD=5k,
∵AD=3,
∴3k=3,解得k=1,
∴BD=5k=5,
由勾股定理得:AB=√(BD²-AD²)=√(5²-3²)=4。
在Rt△BDC中,∠BDC=90°,sin∠DBC=CD/BC=12/13,
设CD=12m,BC=13m(m>0),
由勾股定理得:BD=√(BC²-CD²)=√[(13m)²-(12m)²]=5m,
∵BD=5,
∴5m=5,解得m=1,
∴CD=12m=12,BC=13m=13。
综上,AB=4,BC=13,CD=12。
设AD=3k,BD=5k,
∵AD=3,
∴3k=3,解得k=1,
∴BD=5k=5,
由勾股定理得:AB=√(BD²-AD²)=√(5²-3²)=4。
在Rt△BDC中,∠BDC=90°,sin∠DBC=CD/BC=12/13,
设CD=12m,BC=13m(m>0),
由勾股定理得:BD=√(BC²-CD²)=√[(13m)²-(12m)²]=5m,
∵BD=5,
∴5m=5,解得m=1,
∴CD=12m=12,BC=13m=13。
综上,AB=4,BC=13,CD=12。
13. 在$Rt△ABC$中,已知$∠ACB = 90^{\circ}$,$AC = 13$,$CD是斜边AB$上的高,且$CD = 5$,求$∠B$的四个三角比的值.


答案:
解:在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$CD\perp AB$,
$\therefore \angle ADC=\angle CDB=90^{\circ}$,$\angle A+\angle ACD=90^{\circ}$,$\angle A+\angle B=90^{\circ}$,
$\therefore \angle ACD=\angle B$。
在$Rt\triangle ACD$中,$AC=13$,$CD=5$,
$\therefore AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{13^{2}-5^{2}}=12$。
$\sin\angle ACD=\frac{AD}{AC}=\frac{12}{13}$,$\cos\angle ACD=\frac{CD}{AC}=\frac{5}{13}$,
$\tan\angle ACD=\frac{AD}{CD}=\frac{12}{5}$,$\cot\angle ACD=\frac{CD}{AD}=\frac{5}{12}$。
$\because \angle ACD=\angle B$,
$\therefore \sin B=\frac{12}{13}$,$\cos B=\frac{5}{13}$,$\tan B=\frac{12}{5}$,$\cot B=\frac{5}{12}$。
$\therefore \angle ADC=\angle CDB=90^{\circ}$,$\angle A+\angle ACD=90^{\circ}$,$\angle A+\angle B=90^{\circ}$,
$\therefore \angle ACD=\angle B$。
在$Rt\triangle ACD$中,$AC=13$,$CD=5$,
$\therefore AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{13^{2}-5^{2}}=12$。
$\sin\angle ACD=\frac{AD}{AC}=\frac{12}{13}$,$\cos\angle ACD=\frac{CD}{AC}=\frac{5}{13}$,
$\tan\angle ACD=\frac{AD}{CD}=\frac{12}{5}$,$\cot\angle ACD=\frac{CD}{AD}=\frac{5}{12}$。
$\because \angle ACD=\angle B$,
$\therefore \sin B=\frac{12}{13}$,$\cos B=\frac{5}{13}$,$\tan B=\frac{12}{5}$,$\cot B=\frac{5}{12}$。
14. 如图,在$△ABC$中,已知$∠C = 90^{\circ}$,点$D在BC$上,$BD = 4$,$AD = BC$,$cos∠ADC= \frac{3}{5}$.
(1)求$DC$的长;
(2)求$sinB$的值.

(1)求$DC$的长;
(2)求$sinB$的值.

答案:
【解析】:本题主要考查了解直角三角形的相关知识,包括三角函数的定义和应用,以及勾股定理在直角三角形中的运用。
(1)要求$DC$的长,可以通过在$Rt\bigtriangleup ACD$中利用$\cos\angle ADC$的值以及$AD$的长度来求解。
在$Rt\bigtriangleup ACD$中,已知$\cos\angle ADC = \frac{3}{5}$,根据余弦函数的定义,有$\cos\angle ADC = \frac{DC}{AD}$。
设$DC = 3x$,由于$\cos\angle ADC = \frac{3}{5}$,则$AD = 5x$(这里$x$是一个正实数,用于表示$DC$和$AD$的比例关系)。
已知$BD = 4$,且$AD = BC$,所以$BC = 5x$。
根据线段的和差关系,有$BC = BD + DC$,即$5x = 4 + 3x$。
解这个方程,得到$2x = 4$,从而$x = 2$。
将$x = 2$代入$DC = 3x$,得到$DC = 6$。
(2)要求$\sin B$的值,可以通过在$Rt\bigtriangleup ABC$中利用$AC$和$AB$的长度来求解。
由(1)知$AD = 5× 2=10$,即$BC = 10$,且$DC = 6$。
在$Rt\bigtriangleup ACD$中,利用勾股定理,有$AC = \sqrt{AD^{2} - DC^{2}} = \sqrt{10^{2} - 6^{2}} = \sqrt{100 - 36} = \sqrt{64} = 8$。
在$Rt\bigtriangleup ABC$中,再次利用勾股定理,有$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{8^{2} + 10^{2}} = \sqrt{64 + 100} = \sqrt{164} = 2\sqrt{41}$。
根据正弦函数的定义,有$\sin B = \frac{AC}{AB} = \frac{8}{2\sqrt{41}} = \frac{4\sqrt{41}}{41}$。
【答案】:
(1)$DC = 6$
(2)$\sin B = \frac{4\sqrt{41}}{41}$
(1)要求$DC$的长,可以通过在$Rt\bigtriangleup ACD$中利用$\cos\angle ADC$的值以及$AD$的长度来求解。
在$Rt\bigtriangleup ACD$中,已知$\cos\angle ADC = \frac{3}{5}$,根据余弦函数的定义,有$\cos\angle ADC = \frac{DC}{AD}$。
设$DC = 3x$,由于$\cos\angle ADC = \frac{3}{5}$,则$AD = 5x$(这里$x$是一个正实数,用于表示$DC$和$AD$的比例关系)。
已知$BD = 4$,且$AD = BC$,所以$BC = 5x$。
根据线段的和差关系,有$BC = BD + DC$,即$5x = 4 + 3x$。
解这个方程,得到$2x = 4$,从而$x = 2$。
将$x = 2$代入$DC = 3x$,得到$DC = 6$。
(2)要求$\sin B$的值,可以通过在$Rt\bigtriangleup ABC$中利用$AC$和$AB$的长度来求解。
由(1)知$AD = 5× 2=10$,即$BC = 10$,且$DC = 6$。
在$Rt\bigtriangleup ACD$中,利用勾股定理,有$AC = \sqrt{AD^{2} - DC^{2}} = \sqrt{10^{2} - 6^{2}} = \sqrt{100 - 36} = \sqrt{64} = 8$。
在$Rt\bigtriangleup ABC$中,再次利用勾股定理,有$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{8^{2} + 10^{2}} = \sqrt{64 + 100} = \sqrt{164} = 2\sqrt{41}$。
根据正弦函数的定义,有$\sin B = \frac{AC}{AB} = \frac{8}{2\sqrt{41}} = \frac{4\sqrt{41}}{41}$。
【答案】:
(1)$DC = 6$
(2)$\sin B = \frac{4\sqrt{41}}{41}$
(1)如图1、2所示,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较$18^{\circ}$、$35^{\circ}$、$50^{\circ}$、$62^{\circ}$、$88^{\circ}$这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小:(在空格处填写“<”“>”或“=”)
若$α = 45^{\circ}$,则$sinα$
若$α < 45^{\circ}$,则$sinα$
若$α > 45^{\circ}$,则$sinα$
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:$sin10^{\circ}$,$cos30^{\circ}$,$sin50^{\circ}$,$cos70^{\circ}$.
随着锐角度数的增大,它的正弦值增大,余弦值减小
(2)根据你探索到的规律,试比较$18^{\circ}$、$35^{\circ}$、$50^{\circ}$、$62^{\circ}$、$88^{\circ}$这些锐角的正弦值的大小和余弦值的大小.
$\sin18^{\circ}<\sin35^{\circ}<\sin50^{\circ}<\sin62^{\circ}<\sin88^{\circ}$,$\cos18^{\circ}>\cos35^{\circ}>\cos50^{\circ}>\cos62^{\circ}>\cos88^{\circ}$
(3)比较大小:(在空格处填写“<”“>”或“=”)
若$α = 45^{\circ}$,则$sinα$
=
$cosα$;若$α < 45^{\circ}$,则$sinα$
<
$cosα$;若$α > 45^{\circ}$,则$sinα$
>
$cosα$.(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:$sin10^{\circ}$,$cos30^{\circ}$,$sin50^{\circ}$,$cos70^{\circ}$.
$\sin10^{\circ}<\cos70^{\circ}<\sin50^{\circ}<\cos30^{\circ}$
答案:
【解析】:
(1)由图1,当锐角增大时,$AC$不变,$BC$增大,
$\sin\alpha=\frac{BC}{AB}$随着增大,即正弦值增大,
$\cos\alpha=\frac{AC}{AB}$随着减小,即余弦值减小,
所以,随着锐角度数的增大,它的正弦值增大,余弦值减小。
(2)由(1)知:
$\sin18^{\circ}<\sin35^{\circ}<\sin50^{\circ}<\sin62^{\circ}<\sin88^{\circ}$,
$\cos18^{\circ}>\cos35^{\circ}>\cos50^{\circ}>\cos62^{\circ}>\cos88^{\circ}$。
(3)由(1)知:
若$\alpha=45^{\circ}$,则$\sin\alpha=\frac{\sqrt{2}}{2},\cos\alpha=\frac{\sqrt{2}}{2}$,
则$\sin\alpha=\cos\alpha$;
若$\alpha<45^{\circ}$,则$\sin\alpha<\sin45^{\circ},\cos\alpha>\cos45^{\circ}$,
则$\sin\alpha<\cos\alpha$;
若$\alpha>45^{\circ}$,则$\sin\alpha>\sin45^{\circ},\cos\alpha<\cos45^{\circ}$,
则$\sin\alpha>\cos\alpha$。
(4)因为$\cos30^{\circ}=\sin60^{\circ},\cos70^{\circ}=\sin20^{\circ}$,
所以$\sin10^{\circ}<\cos70^{\circ}<\sin50^{\circ}<\cos30^{\circ}$。
【答案】:
(1)随着锐角度数的增大,它的正弦值增大,余弦值减小;
(2)$\sin18^{\circ}<\sin35^{\circ}<\sin50^{\circ}<\sin62^{\circ}<\sin88^{\circ}$,$\cos18^{\circ}>\cos35^{\circ}>\cos50^{\circ}>\cos62^{\circ}>\cos88^{\circ}$;
(3)$=$;$<$;$>$;
(4)$\sin10^{\circ}<\cos70^{\circ}<\sin50^{\circ}<\cos30^{\circ}$。
(1)由图1,当锐角增大时,$AC$不变,$BC$增大,
$\sin\alpha=\frac{BC}{AB}$随着增大,即正弦值增大,
$\cos\alpha=\frac{AC}{AB}$随着减小,即余弦值减小,
所以,随着锐角度数的增大,它的正弦值增大,余弦值减小。
(2)由(1)知:
$\sin18^{\circ}<\sin35^{\circ}<\sin50^{\circ}<\sin62^{\circ}<\sin88^{\circ}$,
$\cos18^{\circ}>\cos35^{\circ}>\cos50^{\circ}>\cos62^{\circ}>\cos88^{\circ}$。
(3)由(1)知:
若$\alpha=45^{\circ}$,则$\sin\alpha=\frac{\sqrt{2}}{2},\cos\alpha=\frac{\sqrt{2}}{2}$,
则$\sin\alpha=\cos\alpha$;
若$\alpha<45^{\circ}$,则$\sin\alpha<\sin45^{\circ},\cos\alpha>\cos45^{\circ}$,
则$\sin\alpha<\cos\alpha$;
若$\alpha>45^{\circ}$,则$\sin\alpha>\sin45^{\circ},\cos\alpha<\cos45^{\circ}$,
则$\sin\alpha>\cos\alpha$。
(4)因为$\cos30^{\circ}=\sin60^{\circ},\cos70^{\circ}=\sin20^{\circ}$,
所以$\sin10^{\circ}<\cos70^{\circ}<\sin50^{\circ}<\cos30^{\circ}$。
【答案】:
(1)随着锐角度数的增大,它的正弦值增大,余弦值减小;
(2)$\sin18^{\circ}<\sin35^{\circ}<\sin50^{\circ}<\sin62^{\circ}<\sin88^{\circ}$,$\cos18^{\circ}>\cos35^{\circ}>\cos50^{\circ}>\cos62^{\circ}>\cos88^{\circ}$;
(3)$=$;$<$;$>$;
(4)$\sin10^{\circ}<\cos70^{\circ}<\sin50^{\circ}<\cos30^{\circ}$。
查看更多完整答案,请扫码查看


