1. 在$Rt\triangle ABC$中,已知$\angle C = 90^{\circ}$。若$AB = 5$,$AC = 4$,则$\cot A$等于(
A.$\frac{3}{5}$;
B.$\frac{4}{5}$;
C.$\frac{3}{4}$;
D.$\frac{4}{3}$。
D
)A.$\frac{3}{5}$;
B.$\frac{4}{5}$;
C.$\frac{3}{4}$;
D.$\frac{4}{3}$。
答案:
【解析】:
本题主要考察锐角三角比的定义。在直角三角形中,对于任意一个锐角,其余弦($\cos$)、正弦($\sin$)、正切($\tan$)和余切($\cot$)都有特定的定义。对于锐角$A$,其余切$\cot A$定义为邻边长度除以对边长度。在$Rt \bigtriangleup ABC$中,已知$\angle C = 90^{\circ}$,$AB = 5$,$AC = 4$,需要通过勾股定理计算出$BC$的长度,即$BC = \sqrt{AB^{2} - AC^{2}} = \sqrt{5^{2} - 4^{2}} = 3$。然后根据余切的定义,有$\cot A = \frac{AC}{BC} = \frac{4}{3}$。
【答案】:
D. $\frac{4}{3}$。
本题主要考察锐角三角比的定义。在直角三角形中,对于任意一个锐角,其余弦($\cos$)、正弦($\sin$)、正切($\tan$)和余切($\cot$)都有特定的定义。对于锐角$A$,其余切$\cot A$定义为邻边长度除以对边长度。在$Rt \bigtriangleup ABC$中,已知$\angle C = 90^{\circ}$,$AB = 5$,$AC = 4$,需要通过勾股定理计算出$BC$的长度,即$BC = \sqrt{AB^{2} - AC^{2}} = \sqrt{5^{2} - 4^{2}} = 3$。然后根据余切的定义,有$\cot A = \frac{AC}{BC} = \frac{4}{3}$。
【答案】:
D. $\frac{4}{3}$。
2. 在$\triangle ABC$中,已知$\angle C = 90^{\circ}$,$BC = 2$,$\tan A = \frac{2}{3}$,则边$AB$的长是(
A.$\sqrt{13}$;
B.$3$;
C.$\frac{3}{4}$;
D.$\sqrt{5}$。
A
)A.$\sqrt{13}$;
B.$3$;
C.$\frac{3}{4}$;
D.$\sqrt{5}$。
答案:
【解析】:
本题主要考察直角三角形中三角函数的应用以及勾股定理的使用。
在直角三角形$\triangle ABC$中,已知$\angle C = 90^{\circ}$,$BC = 2$,$\tan A = \frac{2}{3}$。
由正切函数的定义,我们有
$\tan A = \frac{BC}{AC} = \frac{2}{3}$
将已知的$BC = 2$代入上式,得到
$\frac{2}{AC} = \frac{2}{3} \implies AC = 3$
接下来,我们使用勾股定理来求边$AB$的长度。
勾股定理公式为$AB^2 = AC^2 + BC^2$,代入$AC = 3$,$BC = 2$,得到
$AB^2 = 3^2 + 2^2 = 9 + 4 = 13$
所以,$AB = \sqrt{13}$。
【答案】:A. $\sqrt{13}$。
本题主要考察直角三角形中三角函数的应用以及勾股定理的使用。
在直角三角形$\triangle ABC$中,已知$\angle C = 90^{\circ}$,$BC = 2$,$\tan A = \frac{2}{3}$。
由正切函数的定义,我们有
$\tan A = \frac{BC}{AC} = \frac{2}{3}$
将已知的$BC = 2$代入上式,得到
$\frac{2}{AC} = \frac{2}{3} \implies AC = 3$
接下来,我们使用勾股定理来求边$AB$的长度。
勾股定理公式为$AB^2 = AC^2 + BC^2$,代入$AC = 3$,$BC = 2$,得到
$AB^2 = 3^2 + 2^2 = 9 + 4 = 13$
所以,$AB = \sqrt{13}$。
【答案】:A. $\sqrt{13}$。
3. 如图,已知$P是\angle \alpha的边OA$上一点,且点$P的坐标为(3,4)$,则$\cot \alpha$的值为(
A.$\frac{3}{5}$;
B.$\frac{4}{5}$;
C.$\frac{3}{4}$;
D.$\frac{4}{3}$。
C
)A.$\frac{3}{5}$;
B.$\frac{4}{5}$;
C.$\frac{3}{4}$;
D.$\frac{4}{3}$。
答案:
【解析】:
本题可根据三角函数的定义来求解$\cot\alpha$的值。
在直角三角形中,对于锐角$\alpha$,余切函数$\cot\alpha$的定义为$\cot\alpha=\frac{邻边}{对边}$。
已知点$P$的坐标为$(3,4)$,过点$P$作$PB\perp x$轴于点$B$,则$OB = 3$,$PB = 4$。
在$Rt\triangle POB$中,$\angle\alpha$的邻边为$OB$,对边为$PB$,根据余切函数的定义可得$\cot\alpha=\frac{OB}{PB}$。
将$OB = 3$,$PB = 4$代入$\cot\alpha=\frac{OB}{PB}$,可得$\cot\alpha=\frac{3}{4}$。
【答案】:C。
本题可根据三角函数的定义来求解$\cot\alpha$的值。
在直角三角形中,对于锐角$\alpha$,余切函数$\cot\alpha$的定义为$\cot\alpha=\frac{邻边}{对边}$。
已知点$P$的坐标为$(3,4)$,过点$P$作$PB\perp x$轴于点$B$,则$OB = 3$,$PB = 4$。
在$Rt\triangle POB$中,$\angle\alpha$的邻边为$OB$,对边为$PB$,根据余切函数的定义可得$\cot\alpha=\frac{OB}{PB}$。
将$OB = 3$,$PB = 4$代入$\cot\alpha=\frac{OB}{PB}$,可得$\cot\alpha=\frac{3}{4}$。
【答案】:C。
4. 已知$\angle A$为锐角,且$\cot A = \frac{5}{12}$,则$\tan A = $
$\frac{12}{5}$
。
答案:
【解析】:
本题主要考察锐角三角函数中的余切和正切的关系。
已知$\cot A = \frac{5}{12}$,根据余切的定义,我们有$\cot A = \frac{\text{邻边}}{\text{对边}}$。
因此,可以设直角三角形中,与角$A$相邻的直角边长度为$5k$,与角$A$相对的直角边长度为$12k$(其中$k > 0$)。
接下来,我们需要求$\tan A$。根据正切的定义,$\tan A = \frac{\text{对边}}{\text{邻边}}$。
将已知的边长代入,得到$\tan A = \frac{12k}{5k} = \frac{12}{5}$。
【答案】:
$\frac{12}{5}$。
本题主要考察锐角三角函数中的余切和正切的关系。
已知$\cot A = \frac{5}{12}$,根据余切的定义,我们有$\cot A = \frac{\text{邻边}}{\text{对边}}$。
因此,可以设直角三角形中,与角$A$相邻的直角边长度为$5k$,与角$A$相对的直角边长度为$12k$(其中$k > 0$)。
接下来,我们需要求$\tan A$。根据正切的定义,$\tan A = \frac{\text{对边}}{\text{邻边}}$。
将已知的边长代入,得到$\tan A = \frac{12k}{5k} = \frac{12}{5}$。
【答案】:
$\frac{12}{5}$。
5. 在$Rt\triangle ABC$中,已知$\angle C = 90^{\circ}$,$\cot A = \frac{3}{5}$,$b = 6$,则$c = $
$2\sqrt{34}$
。
答案:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\cot A = \frac{b}{a} = \frac{3}{5}$。
因为$b = 6$,所以$\frac{6}{a} = \frac{3}{5}$,解得$a = 10$。
由勾股定理得$c = \sqrt{a^2 + b^2} = \sqrt{10^2 + 6^2} = \sqrt{136} = 2\sqrt{34}$。
$2\sqrt{34}$
因为$b = 6$,所以$\frac{6}{a} = \frac{3}{5}$,解得$a = 10$。
由勾股定理得$c = \sqrt{a^2 + b^2} = \sqrt{10^2 + 6^2} = \sqrt{136} = 2\sqrt{34}$。
$2\sqrt{34}$
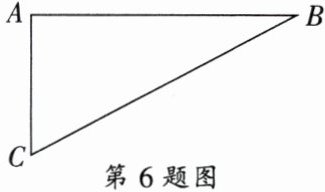
6. 如图,为测一河两岸相对两电线杆$A$、$B$间的距离,在距点$17m的C处(AC\perp AB)测得\angle ACB = 50^{\circ}$,则$A$、$B$间的距离应为______$m$。

20.26
答案:
解:在Rt△ABC中,∠A=90°,AC=17m,∠ACB=50°。
tan∠ACB=AB/AC,
AB=AC·tan∠ACB=17·tan50°≈17×1.1918≈20.26(m)。
20.26
tan∠ACB=AB/AC,
AB=AC·tan∠ACB=17·tan50°≈17×1.1918≈20.26(m)。
20.26
7. 在$\triangle ABC$中,已知$\angle C = 90^{\circ}$,$a$、$b$、$c分别是\angle A$、$\angle B$、$\angle C$的对边长,则$b = $
$\sqrt{c^2 - a^2}$
。(用代数式表示)
答案:
在直角三角形中,根据勾股定理$a^2 + b^2 = c^2$,可得$b^2 = c^2 - a^2$,所以$b = \sqrt{c^2 - a^2}$($b > 0$)。
$\sqrt{c^2 - a^2}$
$\sqrt{c^2 - a^2}$
8. 若直角三角形的斜边长和一条直角边长之比为$25:24$,则其中最小角的正切值是______
$\frac{7}{24}$
。
答案:
【解析】:
本题主要考察直角三角形中三角比的应用。
首先,根据题目描述,设直角三角形的斜边长为$25k$,一条直角边长为$24k$($k > 0$)。
利用勾股定理,可以求出另一条直角边的长度。
勾股定理公式为:$c^2 = a^2 + b^2$,其中$c$是斜边,$a$和$b$是直角边。
设另一条直角边为$b$,则有:
$(25k)^2 = (24k)^2 + b^2$,
$625k^2 = 576k^2 + b^2$,
$b^2 = 49k^2$,
$b = 7k$,
接下来,需要找出直角三角形中最小角的正切值。
正切值的定义为对边长度除以邻边长度。
在这个直角三角形中,最小的角对应的对边是最短的直角边$7k$,邻边是较长的直角边$24k$。
因此,最小角的正切值为:
$\tan(\theta) = \frac{7k}{24k} = \frac{7}{24}$,
【答案】:
$\frac{7}{24}$。
本题主要考察直角三角形中三角比的应用。
首先,根据题目描述,设直角三角形的斜边长为$25k$,一条直角边长为$24k$($k > 0$)。
利用勾股定理,可以求出另一条直角边的长度。
勾股定理公式为:$c^2 = a^2 + b^2$,其中$c$是斜边,$a$和$b$是直角边。
设另一条直角边为$b$,则有:
$(25k)^2 = (24k)^2 + b^2$,
$625k^2 = 576k^2 + b^2$,
$b^2 = 49k^2$,
$b = 7k$,
接下来,需要找出直角三角形中最小角的正切值。
正切值的定义为对边长度除以邻边长度。
在这个直角三角形中,最小的角对应的对边是最短的直角边$7k$,邻边是较长的直角边$24k$。
因此,最小角的正切值为:
$\tan(\theta) = \frac{7k}{24k} = \frac{7}{24}$,
【答案】:
$\frac{7}{24}$。
9. 若直角三角形中较长的直角边长为$30$,这边所对角的余切为$\frac{8}{15}$,则此三角形的周长为
80
,面积为240
。
答案:
【解析】:
本题主要考查直角三角形的三角比定义和计算。在直角三角形中,已知较长的直角边长和该边所对角的余切值,可以通过余切的定义求出另一条直角边的长度,再通过勾股定理求出斜边的长度,最后计算三角形的周长和面积。
设较长的直角边长为$a=30$,较短的直角边长为$b$,斜边长为$c$。
由余切的定义,有$\cot \theta = \frac{b}{a}$,其中$\theta$为较长直角边所对的角。
根据题意,得$\frac{b}{30} = \frac{8}{15}$。
解这个方程,可以得到$b = 16$。
利用勾股定理$a^{2} + b^{2} = c^{2}$,可以求出斜边$c$的长度:
$c = \sqrt{a^{2} + b^{2}} = \sqrt{30^{2} + 16^{2}} = \sqrt{900 + 256} = \sqrt{1156} = 34$,
三角形的周长为$a + b + c = 30 + 16 + 34 = 80$。
三角形的面积为$\frac{1}{2} × a × b = \frac{1}{2} × 30 × 16 = 240$。
【答案】:
周长为$80$;面积为$240$。
本题主要考查直角三角形的三角比定义和计算。在直角三角形中,已知较长的直角边长和该边所对角的余切值,可以通过余切的定义求出另一条直角边的长度,再通过勾股定理求出斜边的长度,最后计算三角形的周长和面积。
设较长的直角边长为$a=30$,较短的直角边长为$b$,斜边长为$c$。
由余切的定义,有$\cot \theta = \frac{b}{a}$,其中$\theta$为较长直角边所对的角。
根据题意,得$\frac{b}{30} = \frac{8}{15}$。
解这个方程,可以得到$b = 16$。
利用勾股定理$a^{2} + b^{2} = c^{2}$,可以求出斜边$c$的长度:
$c = \sqrt{a^{2} + b^{2}} = \sqrt{30^{2} + 16^{2}} = \sqrt{900 + 256} = \sqrt{1156} = 34$,
三角形的周长为$a + b + c = 30 + 16 + 34 = 80$。
三角形的面积为$\frac{1}{2} × a × b = \frac{1}{2} × 30 × 16 = 240$。
【答案】:
周长为$80$;面积为$240$。
10. 如图,将一把梯子的下端放在地面上,它的上端靠着墙面,把墙面和地面所形成的角画成一个直角,梯子画成一条线段$AB$,得到一个$Rt\triangle AOB$。如果将梯子的两端分别沿着墙面和地面滑动,当$\angle A = 30^{\circ}$时,$\frac{OB}{AO} = $

$\frac{\sqrt{3}}{3}$
;当$\angle A = 45^{\circ}$时,$\frac{OB}{AO} = $$1$
。
答案:
解:在$Rt\triangle AOB$中,$\angle AOB = 90^{\circ}$,$\frac{OB}{AO} = \tan\angle A$。
当$\angle A = 30^{\circ}$时,$\tan30^{\circ} = \frac{\sqrt{3}}{3}$,所以$\frac{OB}{AO} = \frac{\sqrt{3}}{3}$。
当$\angle A = 45^{\circ}$时,$\tan45^{\circ} = 1$,所以$\frac{OB}{AO} = 1$。
$\frac{\sqrt{3}}{3}$;$1$
当$\angle A = 30^{\circ}$时,$\tan30^{\circ} = \frac{\sqrt{3}}{3}$,所以$\frac{OB}{AO} = \frac{\sqrt{3}}{3}$。
当$\angle A = 45^{\circ}$时,$\tan45^{\circ} = 1$,所以$\frac{OB}{AO} = 1$。
$\frac{\sqrt{3}}{3}$;$1$
查看更多完整答案,请扫码查看


