《2025年中学生世界九年级数学上册沪教版五四制》

1. 如图,已知$AD⊥BC于点D$,$CE⊥AB于点E$,交$AD于点F$,则图中相似三角形的对数是(D)
A.3;
B.4;
C.5;
D.6.

答案： 解：
∵AD⊥BC，CE⊥AB，
∴∠ADB=∠ADC=∠CEB=∠CEA=90°。
1. 在△ABD和△CBE中，∠B=∠B，∠ADB=∠CEB=90°，
∴△ABD∽△CBE；
2. 在△ABD和△AFE中，∠BAD=∠FAE，∠ADB=∠AEF=90°，
∴△ABD∽△AFE；
3. 由△ABD∽△CBE和△ABD∽△AFE，得△CBE∽△AFE；
4. 在△AEF和△CDF中，∠AEF=∠CDF=90°，∠AFE=∠CFD（对顶角），
∴△AEF∽△CDF；
5. 由△CBE∽△AFE和△AFE∽△CDF，得△CBE∽△CDF；
6. 在△ABD和△CDF中，由△ABD∽△CBE和△CBE∽△CDF，得△ABD∽△CDF。
综上，相似三角形共6对。
答案：D

2. 下列各组图形有可能不相似的是(A)
A.各有一个角是$45^{\circ}$的两个等腰三角形;
B.各有一个角是$60^{\circ}$的两个等腰三角形;
C.各有一个角是$105^{\circ}$的两个等腰三角形;
D.两个等腰直角三角形.

答案： 【解析】：
本题主要考察相似三角形的判定条件。
对于选项A，各有一个角是$45^{\circ}$的两个等腰三角形，这个$45^{\circ}$的角可能是顶角，也可能是底角。
如果是底角，那么另一个底角也是$45^{\circ}$，顶角则是$90^{\circ}$；
如果是顶角，那么两个底角各是$(180^{\circ}-45^{\circ})÷ 2=67.5^{\circ}$。
由于存在两种可能性，所以这两个三角形不一定相似。
对于选项B，各有一个角是$60^{\circ}$的两个等腰三角形，由于等腰三角形的两个底角相等，且三角形内角和为$180^{\circ}$，
如果其中一个角是$60^{\circ}$，那么它只能是顶角（因为两个底角之和已经超过$120^{\circ}$，如果$60^{\circ}$是底角，则另一个底角也是$60^{\circ}$，顶角就是$60^{\circ}$，与等腰三角形的性质矛盾）。
所以，这两个三角形都是等边三角形，因此一定相似。
对于选项C，各有一个角是$105^{\circ}$的两个等腰三角形，这个角只能是顶角（因为两个底角之和必须小于$180^{\circ}-105^{\circ}=75^{\circ}× 2=150^{\circ}$，所以底角不能是$105^{\circ}$）。
由于顶角相等，且都是等腰三角形，所以这两个三角形一定相似。
对于选项D，两个等腰直角三角形，它们的两个底角都是$45^{\circ}$，顶角都是$90^{\circ}$，所以一定相似。
综上所述，只有选项A中的两个等腰三角形不一定相似。
【答案】：
A

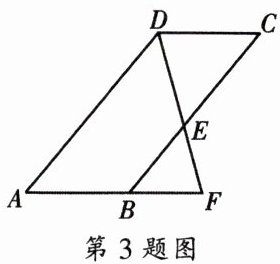
3. 如图,已知点$F在平行四边形ABCD的边AB$的延长线上,联结$DF$,交$BC于点E$,则图中与$\triangle BEF$相似的三角形有(B)

A.1个;
B.2个;
C.3个;
D.4个.

答案： 【解析】：
本题可根据平行四边形的性质以及相似三角形的判定定理来找出与$\triangle BEF$相似的三角形。
步骤一：分析平行四边形的性质
已知四边形$ABCD$是平行四边形，根据平行四边形的性质可知$AB// CD$，$AD// BC$。
步骤二：根据平行关系找相似三角形
找与$\triangle BEF$相似的三角形（利用$AB// CD$）
因为$AB// CD$，所以$BF// CD$，根据“平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似”，可得$\triangle BEF\sim\triangle CDE$。
找与$\triangle BEF$相似的三角形（利用$AD// BC$）
因为$AD// BC$，即$AD// BE$，同理可得$\triangle BEF\sim\triangle ADF$。
综上，与$\triangle BEF$相似的三角形有$\triangle CDE$和$\triangle ADF$，共$2$个。
【答案】：B。

4. 已知两个三角形相似,其中一个三角形的两个角分别为$72^{\circ}$、$63^{\circ}$,则另一个三角形的最小的内角为$45^{\circ}$.

答案： 【解析】：
本题主要考查相似三角形的性质，即相似三角形的对应角相等。
首先，根据三角形内角和为$180^{\circ}$的性质，我们可以求出给定三角形的第三个角。
已知两个角分别为$72^{\circ}$和$63^{\circ}$，则第三个角为：
$180^{\circ} - 72^{\circ} - 63^{\circ} = 45^{\circ}$
由于两个三角形相似，根据相似三角形的性质，它们的对应角必须相等。
因此，另一个三角形的三个角也分别为$72^{\circ}$、$63^{\circ}$和$45^{\circ}$。
其中，最小的内角为$45^{\circ}$。
【答案】：
$45^{\circ}$

5. 如图,已知点$D$、$E分别在\triangle ABC的边AB$、$AC$上,且$∠AED= ∠B$.若$AB= 7$,$AC= 4$,$AD= 2$,则$AE= $$\frac{7}{2}$.

答案： 【解析】：
本题主要考查相似三角形的判定和性质。
因为$\angle AED=\angle B$，并且$\angle A$为公共角，
根据相似三角形的判定定理：
如果两个三角形的两个角分别对应相等，那么这两个三角形相似，
可得$\triangle AED\sim \triangle ABC$，
由于相似三角形的对应边成比例，
可得$\frac{AE}{AB}=\frac{AD}{AC}$，
将已知的边长代入比例式中，得到$\frac{AE}{7}=\frac{2}{4}$，
解这个比例式，得到$AE=\frac{7}{2}$。
【答案】：
$\frac{7}{2}$

6. 如图,已知$AB$、$CD相交于点O$,且$∠A= ∠C$.若$OA= 3$,$OD= 4$,$OB= 2$,则$OC= $1.5.

答案： 【解析】：
由题可知，该题需要证明三角形相似，需要用到相似三角形的判定定理，即如果两个三角形的两个角分别对应相等，‌那么这两个三角形相似，
已知$AB$，$CD$相交于点$O$，
所以$\angle AOD=\angle COB$，
因为$\angle A=\angle C$，
所以$\triangle AOD\sim \triangle COB$，
根据相似三角形的性质，可得$\frac{OA}{OC}=\frac{OD}{OB}$，
已知$OA=3$，$OD=4$，$OB=2$，
所以$\frac{3}{OC}=\frac{4}{2}$，
解得$OC=1.5$。
【答案】：
$1.5$。

7. 如图,在$□ ABCD$中,$AE= EB$,$AF= 3$,则$FC= $6.

答案： 【解析】：本题可根据平行四边形的性质以及相似三角形的判定和性质来求解$FC$的长度。
步骤一：分析已知条件
已知四边形$ABCD$是平行四边形，根据平行四边形的性质可知$AB// CD$，$AB = CD$。
因为$AE = EB$，所以$AE=\frac{1}{2}AB$，又因为$AB = CD$，所以$AE=\frac{1}{2}CD$。
步骤二：证明三角形相似
由于$AB// CD$，即$AE// CD$，那么$\triangle AEF$和$\triangle CDF$中，$\angle FAE=\angle FCD$，$\angle FEA=\angle FDC$（两直线平行，内错角相等）。
根据两角分别相等的两个三角形相似，可得$\triangle AEF\sim\triangle CDF$。
步骤三：根据相似三角形的性质列比例式
相似三角形对应边成比例，因为$\triangle AEF\sim\triangle CDF$，所以$\frac{AF}{FC}=\frac{AE}{CD}$。
由$AE=\frac{1}{2}CD$，可得$\frac{AE}{CD}=\frac{1}{2}$，即$\frac{AF}{FC}=\frac{1}{2}$。
步骤四：求解$FC$的长度
已知$AF = 3$，将其代入$\frac{AF}{FC}=\frac{1}{2}$中，得到$\frac{3}{FC}=\frac{1}{2}$，交叉相乘可得$FC = 3×2 = 6$。
【答案】：$6$