《2025年中学生世界九年级数学上册沪教版五四制》

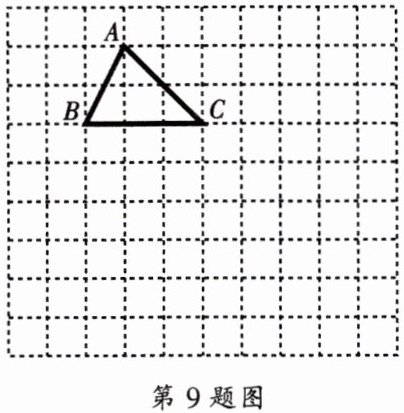
9. 如图,请在方格图中画出一个与 $ \triangle ABC $ 相似且相似比不为 $ 1 $ 的 $ \triangle DEF $. ($ D $、$ E $、$ F $ 必须在方格图的交叉点上)

答案： 解：
1. 计算△ABC各边长：设方格边长为1，AB=√[(1-0)²+(2-1)²]=√2，BC=3，AC=√[(3-1)²+(1-2)²]=√5。
2. 取相似比为2，放大后边长：DE=2√2，EF=6，DF=2√5。
3. 在方格中确定点D(5,0)，E(5,6)，F(9,2)，连接D、E、F得△DEF。
（注：图中D、E、F需在交叉点上，具体坐标可调整，满足相似比不为1即可。）
（此处需根据方格图实际绘制△DEF，文字描述坐标仅为示例。）

10. 在下列方格图中,分别画出 $ \triangle ABC $ 和四边形 $ ABCD $ 的一个相似图形.

答案： 【解析】：
题目考查了相似图形的画法，对于相似图形，对应角相等，对应边成比例，我们可以选择一个合适的相似比，比如$2:1$，然后根据这个相似比在方格图中画出相似图形，对于$\triangle ABC$，先确定其各顶点的位置，然后按照相似比确定新三角形各顶点的位置并连接，对于四边形$ABCD$，同样先确定各顶点位置，再按相似比确定新四边形各顶点位置并连接。
【答案】：
图略（在方格图中，对于$\triangle ABC$，以$A$点为例，假设原$A$点坐标对应的方格位置，按照相似比$2:1$，新$A$点在相应方向上距离原点的方格数变为原来的$2$倍，同理确定$B$、$C$的新位置，连接新三点得到相似三角形；对于四边形$ABCD$，同样按此方法确定$A$、$B$、$C$、$D$的新位置，连接新四点得到相似四边形）。

11. 如图,已知矩形外框的长、宽分别为 $ 12 $, $ 6 $.
(1)当 $ x = y = 2 $ 时,矩形内、外框相似吗? 请说明理由;
(2)请取一对符合条件的 $ x $, $ y $ 的值,使矩形内、外框相似.

答案：
(1)不相似。理由：当$x = y = 2$时，内框矩形的长为$12 - 2y=12 - 2×2 = 8$，宽为$6 - 2x=6 - 2×2 = 2$。外框矩形长与宽的比为$12:6 = 2:1$，内框矩形长与宽的比为$8:2 = 4:1$。因为$2:1≠4:1$，所以矩形内、外框不相似。
(2)设内框矩形的长为$12 - 2y$，宽为$6 - 2x$。要使内、外框相似，则$\frac{12 - 2y}{12}=\frac{6 - 2x}{6}$，化简得$12 - 2y = 2(6 - 2x)$，即$12 - 2y = 12 - 4x$，所以$2y = 4x$，即$y = 2x$。取$x = 1$，则$y = 2$（答案不唯一）。

思维与拓展 1
如图,在下列方格图中,将等腰三角形 $ ABC $ 缩小,缩小后图形对应线段的比值为 $ \frac{1}{2} $.
(1) 画出缩小后的相似图形 $ \triangle A'B'C' $;
(2) 若每个小方格的边长为 $ 1 $,试计算 $ \triangle A'B'C' $ 的面积 $ S $;
(3) 比较两个三角形面积的比值和对应边的比值,你有怎样的发现?

答案：
(1) 图略（以点A为位似中心，分别取AB、AC中点A'、B'、C'，连接A'B'、B'C'、C'A'；或以点B为位似中心，或其他位似中心，按比例缩小）。
(2) 解：由图可知原等腰三角形ABC的底BC长为6，高为6，面积为$\frac{1}{2}×6×6=18$。因为缩小后对应线段比值为$\frac{1}{2}$，所以面积比为$(\frac{1}{2})^2=\frac{1}{4}$，则$\triangle A'B'C'$的面积$S=18×\frac{1}{4}=4.5$。
(3) 两个三角形面积的比值等于对应边比值的平方。