《2025年中学生世界九年级数学上册沪教版五四制》

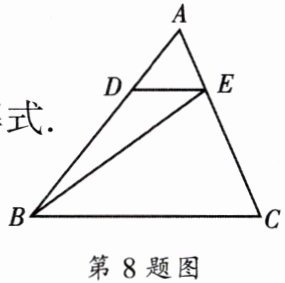
8. 如图,已知点$D$、$E分别在\triangle ABC的边AB$、$AC$上,$DE// BC$,$AD= \frac {1}{2}DB$,如果向量$\overrightarrow {BA}= \overrightarrow {a}$,向量$\overrightarrow {BC}= \overrightarrow {b}$.
(1)试用$\overrightarrow {a}$、$\overrightarrow {b}表示向量\overrightarrow {AE}$;
(2)求作:向量$\overrightarrow {BE}在向量\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量,写出向量$\overrightarrow {BE}关于\overrightarrow {a}$、$\overrightarrow {b}$的分解式.

答案： 【解析】：本题主要考查平面向量的线性运算以及向量的分解。
（1）因为$DE// BC$，根据平行线分线段成比例定理，可得$\frac{AD}{DB}=\frac{AE}{EC}$。
已知$AD = \frac{1}{2}DB$，则$\frac{AD}{DB}=\frac{1}{2}$，所以$\frac{AE}{EC}=\frac{1}{2}$，即$EC = 2AE$，那么$AC=AE + EC = 3AE$。
因为$\overrightarrow{BC}=\overrightarrow{b}$，$\overrightarrow{BA}=\overrightarrow{a}$，且$\overrightarrow{AC}=\overrightarrow{BC}-\overrightarrow{BA}=\overrightarrow{b}-\overrightarrow{a}$。
又因为$\overrightarrow{AE}=\frac{1}{3}\overrightarrow{AC}$，所以$\overrightarrow{AE}=\frac{1}{3}(\overrightarrow{b}-\overrightarrow{a})=-\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$。
（2）因为$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}$，由（1）知$\overrightarrow{AE}=-\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$，且$\overrightarrow{BA}=\overrightarrow{a}$，所以$\overrightarrow{BE}=\overrightarrow{a}+(-\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b})=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$。
向量$\overrightarrow{BE}$在向量$\overrightarrow{a}$方向上的分向量：
与$\overrightarrow{a}$共线且长度为$\vert\frac{2}{3}\overrightarrow{a}\vert$的向量，方向与$\overrightarrow{a}$相同，即$\frac{2}{3}\overrightarrow{a}$。
向量$\overrightarrow{BE}$在向量$\overrightarrow{b}$方向上的分向量：
与$\overrightarrow{b}$共线且长度为$\vert\frac{1}{3}\overrightarrow{b}\vert$的向量，方向与$\overrightarrow{b}$相同，即$\frac{1}{3}\overrightarrow{b}$。
【答案】：
(1)$\overrightarrow {AE}=-\frac {1}{3}\overrightarrow {a}+\frac {1}{3}\overrightarrow {b}$；
(2)向量$\overrightarrow {BE}$在向量$\overrightarrow {a}$方向上的分向量为$\frac {2}{3}\overrightarrow {a}$，在向量$\overrightarrow {b}$方向上的分向量为$\frac {1}{3}\overrightarrow {b}$，$\overrightarrow {BE}=\frac {2}{3}\overrightarrow {a}+\frac {1}{3}\overrightarrow {b}$。

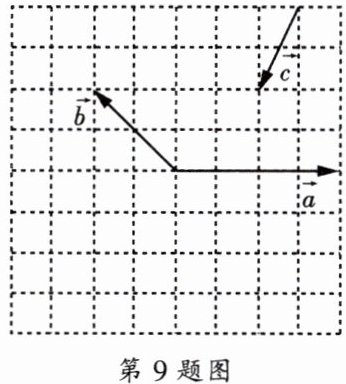
9. 如图,已知非零向量$\overrightarrow {a}$、$\overrightarrow {b}$、$\overrightarrow {c}$.
(1)求作:$\frac {1}{2}\overrightarrow {a}+\overrightarrow {b}$;
(2)求作:向量$\overrightarrow {c}分别在\overrightarrow {a}$、$\overrightarrow {b}$方向上的分向量.(不写作法,但须说明结论)

答案： 1. （1）
解：
首先，取向量$\overrightarrow{a}$的中点$A$，则$\overrightarrow{OA}=\frac{1}{2}\overrightarrow{a}$（$O$为$\overrightarrow{a}$的起点）。
然后，以$\frac{1}{2}\overrightarrow{a}$的终点$A$为起点，作向量$\overrightarrow{AB}=\overrightarrow{b}$。
最后，向量$\overrightarrow{OB}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$（根据向量加法的三角形法则：$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$）。
2. （2）
解：
过向量$\overrightarrow{c}$的终点分别作平行于$\overrightarrow{a}$和$\overrightarrow{b}$的直线，与$\overrightarrow{a}$、$\overrightarrow{b}$所在直线（或其延长线）相交。
设与$\overrightarrow{a}$方向平行的分向量为$\overrightarrow{c_1}$，与$\overrightarrow{b}$方向平行的分向量为$\overrightarrow{c_2}$，则$\overrightarrow{c}=\overrightarrow{c_1}+\overrightarrow{c_2}$，其中$\overrightarrow{c_1}$是$\overrightarrow{c}$在$\overrightarrow{a}$方向上的分向量，$\overrightarrow{c_2}$是$\overrightarrow{c}$在$\overrightarrow{b}$方向上的分向量。

如图,等腰三角形$ABC$中,$AB= AC$,点$P在边BC$上,点$E在边AC$上,$∠BPD= ∠CPE$,在线段$EA上取点F$,使得$EF= BD$.
(1) 求证:$PE// BF$;
(2) 若$CP:BP= 1:3$,$\overrightarrow {PC}= \overrightarrow {a}$,$\overrightarrow {EC}= \overrightarrow {b}$,试用$\overrightarrow {a}$、$\overrightarrow {b}表示\overrightarrow {BF}$.

答案：
(1) 证明：
∵AB=AC，
∴∠ABC=∠ACB。
∵∠BPD=∠CPE，
∴△BPD∽△CPE。
∴$\frac{BD}{CE}=\frac{BP}{CP}$。
∵EF=BD，
∴$\frac{EF}{CE}=\frac{BP}{CP}$，即$\frac{EF}{EC}=\frac{BP}{PC}$。
又∠FEC=∠PCE，
∴△FEC∽△PBC。
∴∠EFC=∠BPC，
∴PE//BF。
(2) 解：
∵CP:BP=1:3，$\overrightarrow{PC}=\overrightarrow{a}$，
∴$\overrightarrow{BP}=3\overrightarrow{PC}=-3\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{BP}+\overrightarrow{PC}=-2\overrightarrow{a}$。
∵△BPD∽△CPE，$\frac{BD}{CE}=\frac{BP}{CP}=3$，
∴BD=3CE。
∵EF=BD，
∴EF=3CE。
∵$\overrightarrow{EC}=\overrightarrow{b}$，
∴$\overrightarrow{EF}=3\overrightarrow{EC}=3\overrightarrow{b}$，$\overrightarrow{FC}=\overrightarrow{FE}+\overrightarrow{EC}=-3\overrightarrow{b}+\overrightarrow{b}=-2\overrightarrow{b}$。
∵AB=AC，△FEC∽△PBC，$\frac{FC}{BC}=\frac{EC}{PC}=1$，
∴FC=BC。
$\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{CF}=-2\overrightarrow{a}+2\overrightarrow{b}$。
答案：
(2)$\overrightarrow{BF}=-2\overrightarrow{a}+2\overrightarrow{b}$