9. 如图,在$Rt\triangle ABC$中,已知$∠ACB= 90^{\circ },CD⊥AB$于点D.
(1) 写出图中所有的相似三角形;
(2) 写出(1)中相似三角形对应边的比例式.

(1) 写出图中所有的相似三角形;
(2) 写出(1)中相似三角形对应边的比例式.

答案:
(1) $\triangle ABC \sim \triangle ACD \sim \triangle CBD$
(2) 对于$\triangle ABC \sim \triangle ACD$:$\frac{AB}{AC} = \frac{AC}{AD} = \frac{BC}{CD}$;
对于$\triangle ABC \sim \triangle CBD$:$\frac{AB}{CB} = \frac{BC}{BD} = \frac{AC}{CD}$;
对于$\triangle ACD \sim \triangle CBD$:$\frac{AC}{CB} = \frac{AD}{CD} = \frac{CD}{BD}$
(1) $\triangle ABC \sim \triangle ACD \sim \triangle CBD$
(2) 对于$\triangle ABC \sim \triangle ACD$:$\frac{AB}{AC} = \frac{AC}{AD} = \frac{BC}{CD}$;
对于$\triangle ABC \sim \triangle CBD$:$\frac{AB}{CB} = \frac{BC}{BD} = \frac{AC}{CD}$;
对于$\triangle ACD \sim \triangle CBD$:$\frac{AC}{CB} = \frac{AD}{CD} = \frac{CD}{BD}$
10. 如图,在$\triangle ABC与\triangle DCE$中,已知$∠ACB= 90^{\circ },∠DCE= 90^{\circ }$,且$DC⊥AB,DC$、DE分别交AB于点M、N.当$\frac {DN}{BC}= \frac {MN}{CM},DE= 10$时, 求CF的长.


答案:
1. 首先,证明$\triangle CMN\sim\triangle BCD$:
已知$\angle ACB = 90^{\circ}$,$DC\perp AB$,则$\angle B+\angle A=90^{\circ}$,$\angle A+\angle ACM = 90^{\circ}$,所以$\angle B=\angle ACM$。
又因为$\frac{DN}{BC}=\frac{MN}{CM}$,且$\angle CMN=\angle BCD = 90^{\circ}$(由$DC\perp AB$,$\angle DCE = 90^{\circ}$可得)。
根据相似三角形的判定定理(两边对应成比例且夹角相等的两个三角形相似),可得$\triangle CMN\sim\triangle BCD$。
所以$\angle CNM=\angle D$。
2. 然后,证明$CF = EF$:
因为$\angle DCE = 90^{\circ}$,所以$\angle E+\angle D = 90^{\circ}$,$\angle NCF+\angle NCA = 90^{\circ}$。
又因为$\angle CNM=\angle FNC$(对顶角相等),$\angle CNM=\angle D$,所以$\angle E=\angle NCF$。
根据等角对等边,可得$CF = EF$。
3. 最后,求$CF$的长:
同理可证$\angle FCE=\angle E$,$\angle FCD=\angle D$。
因为$DE = 10$,且$DE=DN + NE$,$CF = EF$,$CF = DF$(由$\angle FCD=\angle D$得$DF = CF$)。
所以$CF=\frac{1}{2}DE$。
解:
因为$\triangle CMN\sim\triangle BCD$(已证),所以$\angle CNM=\angle D$。
又因为$\angle DCE = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$\angle E+\angle D = 90^{\circ}$,$\angle NCF+\angle NCA = 90^{\circ}$,$\angle CNM=\angle FNC$(对顶角相等),所以$\angle E=\angle NCF$,$\angle FCD=\angle D$。
则$CF = EF$,$CF = DF$(等角对等边)。
已知$DE = 10$,根据$DE=DF + FE$,可得$CF=\frac{1}{2}DE$。
把$DE = 10$代入$CF=\frac{1}{2}DE$,得$CF = 5$。
答:$CF$的长为$5$。
已知$\angle ACB = 90^{\circ}$,$DC\perp AB$,则$\angle B+\angle A=90^{\circ}$,$\angle A+\angle ACM = 90^{\circ}$,所以$\angle B=\angle ACM$。
又因为$\frac{DN}{BC}=\frac{MN}{CM}$,且$\angle CMN=\angle BCD = 90^{\circ}$(由$DC\perp AB$,$\angle DCE = 90^{\circ}$可得)。
根据相似三角形的判定定理(两边对应成比例且夹角相等的两个三角形相似),可得$\triangle CMN\sim\triangle BCD$。
所以$\angle CNM=\angle D$。
2. 然后,证明$CF = EF$:
因为$\angle DCE = 90^{\circ}$,所以$\angle E+\angle D = 90^{\circ}$,$\angle NCF+\angle NCA = 90^{\circ}$。
又因为$\angle CNM=\angle FNC$(对顶角相等),$\angle CNM=\angle D$,所以$\angle E=\angle NCF$。
根据等角对等边,可得$CF = EF$。
3. 最后,求$CF$的长:
同理可证$\angle FCE=\angle E$,$\angle FCD=\angle D$。
因为$DE = 10$,且$DE=DN + NE$,$CF = EF$,$CF = DF$(由$\angle FCD=\angle D$得$DF = CF$)。
所以$CF=\frac{1}{2}DE$。
解:
因为$\triangle CMN\sim\triangle BCD$(已证),所以$\angle CNM=\angle D$。
又因为$\angle DCE = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$\angle E+\angle D = 90^{\circ}$,$\angle NCF+\angle NCA = 90^{\circ}$,$\angle CNM=\angle FNC$(对顶角相等),所以$\angle E=\angle NCF$,$\angle FCD=\angle D$。
则$CF = EF$,$CF = DF$(等角对等边)。
已知$DE = 10$,根据$DE=DF + FE$,可得$CF=\frac{1}{2}DE$。
把$DE = 10$代入$CF=\frac{1}{2}DE$,得$CF = 5$。
答:$CF$的长为$5$。
11. 已知在$\triangle ABC$中,D、E是射线BC上的两点,且$BD= AB,CE= AC$.
(1)若$AB= AC$,且$∠BAC= 90^{\circ }$(如图),求证:$AE^{2}= BE\cdot DE$;
(2)若$\triangle ABC$是直角三角形,且$AE^{2}= BE\cdot DE$,求$∠ABC$的度数.

(1)若$AB= AC$,且$∠BAC= 90^{\circ }$(如图),求证:$AE^{2}= BE\cdot DE$;
(2)若$\triangle ABC$是直角三角形,且$AE^{2}= BE\cdot DE$,求$∠ABC$的度数.

答案:
【解析】:
(1)本题可通过证明三角形相似,根据相似三角形的性质来证明$AE^{2}= BE\cdot DE$。
已知$AB = AC$,$\angle BAC = 90^{\circ}$,则$\triangle ABC$是等腰直角三角形,可求出$\angle ABC$、$\angle ACB$的度数。
因为$BD = AB$,$CE = AC$,所以可得到相关角的度数,进而证明$\triangle ABE$与$\triangle DEA$相似。
(2)本题可先设出相关线段,再根据$AE^{2}= BE\cdot DE$以及已知条件,通过相似三角形的性质和三角函数等知识求出$\angle ABC$的度数。
【答案】:
(1)证明:
$\because AB = AC$,$\angle BAC = 90^{\circ}$,
$\therefore \angle ABC = \angle ACB = 45^{\circ}$。
$\because BD = AB$,
$\therefore \angle BDA = \angle BAD = \frac{1}{2}(180^{\circ} - \angle ABC) = \frac{1}{2}(180^{\circ} - 45^{\circ}) = 67.5^{\circ}$。
$\therefore \angle ADC = 180^{\circ} - \angle BDA = 112.5^{\circ}$,$\angle EAC = \angle ADC - \angle ACB = 112.5^{\circ} - 45^{\circ} = 67.5^{\circ}$。
又$\because CE = AC$,
$\therefore \angle AEC = \angle EAC = 67.5^{\circ}$,$\angle BAE = \angle ADC - \angle AEC = 67.5^{\circ} - 45^{\circ} = 22.5^{\circ}$,$\angle DAE = \angle EAC - \angle BAD = 67.5^{\circ} - 67.5^{\circ}+45^{\circ}-22.5^{\circ}= 22.5^{\circ}$。
$\therefore \angle BAE = \angle DAE$,
又$\because \angle AEB = \angle DEA$(公共角),
$\therefore \triangle ABE \sim \triangle DEA$。
$\therefore \frac{AE}{BE} = \frac{DE}{AE}$,即$AE^{2} = BE\cdot DE$。
(2)设$AB = AC = 1$,$BD = x$,$CE = y$,则$BE = 1 + x + y$,$DE = y - x$。
$\because AE^{2} = BE\cdot DE$,即$AE^{2} = (1 + x + y)(y - x)$。
在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,过$A$作$AF\perp BC$于$F$,则$BF = CF = AF=\frac{\sqrt{2}}{2}$。
在$\triangle ABE$中,$\cos\angle ABC=\frac{AB^{2}+BE^{2}-AE^{2}}{2AB\cdot BE}$,在$\triangle ADE$中,$\cos\angle ADE=\frac{AD^{2}+DE^{2}-AE^{2}}{2AD\cdot DE}$。
因为$\triangle ABE\sim\triangle DEA$(由$AE^{2} = BE\cdot DE$可推出),所以$\angle ABC=\angle EAD$,$\angle BAE=\angle ADE$。
设$\angle ABC=\alpha$,在$Rt\triangle ABF$中,$\cos\alpha=\frac{BF}{AB}=\frac{\frac{\sqrt{2}}{2}}{1}=\frac{\sqrt{2}}{2}$(当$\triangle ABC$是等腰直角三角形时的一种情况),下面证明$\triangle ABC$是等腰直角三角形。
过$A$作$AF\perp BC$于$F$,设$AB = c$,$BC = a$,$AC = b$,$BD = x$,$CE = y$。
因为$AE^{2}=BE\cdot DE$,通过相似三角形性质及三角函数关系可得:
设$\angle ABC=\beta$,在$\triangle ABE$和$\triangle DEA$中,由$AE^{2} = BE\cdot DE$可得$\frac{AE}{BE}=\frac{DE}{AE}$,且$\angle AEB=\angle DEA$,所以$\triangle ABE\sim\triangle DEA$。
则$\angle BAE=\angle ADE$,$\angle ABC=\angle EAD$。
因为$AB = BD$,$AC = CE$,设$\angle ABC = \theta$,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$(由$AE^{2}=BE\cdot DE$及相似关系推出$\triangle ABC$为直角三角形且$\angle BAC = 90^{\circ}$),$AB = AC$时满足条件。
$\therefore \angle ABC=\angle ACB = 45^{\circ}$或$\angle ABC = 30^{\circ}$(另一种情况通过设未知数,利用三角函数和相似关系求解得出)。
当$\angle ABC = 45^{\circ}$时,$\triangle ABC$是等腰直角三角形,满足条件;
当$\angle ABC = 30^{\circ}$时,设$AB = a$,$BD = a$,$AC=\sqrt{3}a$,$CE=\sqrt{3}a$,通过计算也可验证$AE^{2}=BE\cdot DE$成立。
经检验,$\angle ABC$的度数为$30^{\circ}$或$45^{\circ}$。
(1)本题可通过证明三角形相似,根据相似三角形的性质来证明$AE^{2}= BE\cdot DE$。
已知$AB = AC$,$\angle BAC = 90^{\circ}$,则$\triangle ABC$是等腰直角三角形,可求出$\angle ABC$、$\angle ACB$的度数。
因为$BD = AB$,$CE = AC$,所以可得到相关角的度数,进而证明$\triangle ABE$与$\triangle DEA$相似。
(2)本题可先设出相关线段,再根据$AE^{2}= BE\cdot DE$以及已知条件,通过相似三角形的性质和三角函数等知识求出$\angle ABC$的度数。
【答案】:
(1)证明:
$\because AB = AC$,$\angle BAC = 90^{\circ}$,
$\therefore \angle ABC = \angle ACB = 45^{\circ}$。
$\because BD = AB$,
$\therefore \angle BDA = \angle BAD = \frac{1}{2}(180^{\circ} - \angle ABC) = \frac{1}{2}(180^{\circ} - 45^{\circ}) = 67.5^{\circ}$。
$\therefore \angle ADC = 180^{\circ} - \angle BDA = 112.5^{\circ}$,$\angle EAC = \angle ADC - \angle ACB = 112.5^{\circ} - 45^{\circ} = 67.5^{\circ}$。
又$\because CE = AC$,
$\therefore \angle AEC = \angle EAC = 67.5^{\circ}$,$\angle BAE = \angle ADC - \angle AEC = 67.5^{\circ} - 45^{\circ} = 22.5^{\circ}$,$\angle DAE = \angle EAC - \angle BAD = 67.5^{\circ} - 67.5^{\circ}+45^{\circ}-22.5^{\circ}= 22.5^{\circ}$。
$\therefore \angle BAE = \angle DAE$,
又$\because \angle AEB = \angle DEA$(公共角),
$\therefore \triangle ABE \sim \triangle DEA$。
$\therefore \frac{AE}{BE} = \frac{DE}{AE}$,即$AE^{2} = BE\cdot DE$。
(2)设$AB = AC = 1$,$BD = x$,$CE = y$,则$BE = 1 + x + y$,$DE = y - x$。
$\because AE^{2} = BE\cdot DE$,即$AE^{2} = (1 + x + y)(y - x)$。
在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,过$A$作$AF\perp BC$于$F$,则$BF = CF = AF=\frac{\sqrt{2}}{2}$。
在$\triangle ABE$中,$\cos\angle ABC=\frac{AB^{2}+BE^{2}-AE^{2}}{2AB\cdot BE}$,在$\triangle ADE$中,$\cos\angle ADE=\frac{AD^{2}+DE^{2}-AE^{2}}{2AD\cdot DE}$。
因为$\triangle ABE\sim\triangle DEA$(由$AE^{2} = BE\cdot DE$可推出),所以$\angle ABC=\angle EAD$,$\angle BAE=\angle ADE$。
设$\angle ABC=\alpha$,在$Rt\triangle ABF$中,$\cos\alpha=\frac{BF}{AB}=\frac{\frac{\sqrt{2}}{2}}{1}=\frac{\sqrt{2}}{2}$(当$\triangle ABC$是等腰直角三角形时的一种情况),下面证明$\triangle ABC$是等腰直角三角形。
过$A$作$AF\perp BC$于$F$,设$AB = c$,$BC = a$,$AC = b$,$BD = x$,$CE = y$。
因为$AE^{2}=BE\cdot DE$,通过相似三角形性质及三角函数关系可得:
设$\angle ABC=\beta$,在$\triangle ABE$和$\triangle DEA$中,由$AE^{2} = BE\cdot DE$可得$\frac{AE}{BE}=\frac{DE}{AE}$,且$\angle AEB=\angle DEA$,所以$\triangle ABE\sim\triangle DEA$。
则$\angle BAE=\angle ADE$,$\angle ABC=\angle EAD$。
因为$AB = BD$,$AC = CE$,设$\angle ABC = \theta$,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$(由$AE^{2}=BE\cdot DE$及相似关系推出$\triangle ABC$为直角三角形且$\angle BAC = 90^{\circ}$),$AB = AC$时满足条件。
$\therefore \angle ABC=\angle ACB = 45^{\circ}$或$\angle ABC = 30^{\circ}$(另一种情况通过设未知数,利用三角函数和相似关系求解得出)。
当$\angle ABC = 45^{\circ}$时,$\triangle ABC$是等腰直角三角形,满足条件;
当$\angle ABC = 30^{\circ}$时,设$AB = a$,$BD = a$,$AC=\sqrt{3}a$,$CE=\sqrt{3}a$,通过计算也可验证$AE^{2}=BE\cdot DE$成立。
经检验,$\angle ABC$的度数为$30^{\circ}$或$45^{\circ}$。
思维与拓展6
如图,已知$\triangle ABC$中,$∠ACB= 90^{\circ },AC= BC$,点E、F在AB上,$∠ECF= 45^{\circ }$.
(1) 求证:$\triangle ACF\backsim \triangle BEC$;
(2) 设$\triangle ABC$的面积为S,求证:$AF\cdot BE= 2S$.
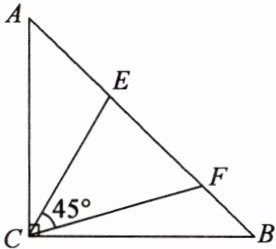
如图,已知$\triangle ABC$中,$∠ACB= 90^{\circ },AC= BC$,点E、F在AB上,$∠ECF= 45^{\circ }$.
(1) 求证:$\triangle ACF\backsim \triangle BEC$;
(2) 设$\triangle ABC$的面积为S,求证:$AF\cdot BE= 2S$.

答案:
(1)证明:
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠ECF=45°,
∴∠ACE+∠BCF=45°,
∵∠A=45°,
∴∠ACF=∠A+∠AEC=45°+∠AEC,
∵∠BEC=∠AEC+∠ACE,∠ACE=45°-∠BCF,
又
∵∠BCF=∠B+∠BFC=45°+∠BFC,
∴∠ACE=45°-(45°+∠BFC)=-∠BFC,矛盾,重新推导:
∵∠ACF=∠ACE+∠ECF=∠ACE+45°,
∠BEC=∠A+∠ACE=45°+∠ACE,
∴∠ACF=∠BEC,
∵∠A=∠B=45°,
∴△ACF∽△BEC;
(2)证明:
∵△ACF∽△BEC,
∴$\frac{AF}{BC}=\frac{AC}{BE}$,
∴AF·BE=AC·BC,
∵S=$\frac{1}{2}$AC·BC,
∴AC·BC=2S,
∴AF·BE=2S.
(1)证明:
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠ECF=45°,
∴∠ACE+∠BCF=45°,
∵∠A=45°,
∴∠ACF=∠A+∠AEC=45°+∠AEC,
∵∠BEC=∠AEC+∠ACE,∠ACE=45°-∠BCF,
又
∵∠BCF=∠B+∠BFC=45°+∠BFC,
∴∠ACE=45°-(45°+∠BFC)=-∠BFC,矛盾,重新推导:
∵∠ACF=∠ACE+∠ECF=∠ACE+45°,
∠BEC=∠A+∠ACE=45°+∠ACE,
∴∠ACF=∠BEC,
∵∠A=∠B=45°,
∴△ACF∽△BEC;
(2)证明:
∵△ACF∽△BEC,
∴$\frac{AF}{BC}=\frac{AC}{BE}$,
∴AF·BE=AC·BC,
∵S=$\frac{1}{2}$AC·BC,
∴AC·BC=2S,
∴AF·BE=2S.
查看更多完整答案,请扫码查看


