11. 求适合下列条件的锐角:
(1)$\sin 2\alpha =\frac {\sqrt {2}}{2}$; (2)$6\cos (\alpha -16^{\circ })= 3\sqrt {3}$.
(1)$\sin 2\alpha =\frac {\sqrt {2}}{2}$; (2)$6\cos (\alpha -16^{\circ })= 3\sqrt {3}$.
答案:
(1)解:因为α为锐角,所以0°<α<90°,则0°<2α<180°。
因为sin2α=$\frac{\sqrt{2}}{2}$,所以2α=45°或2α=135°,
解得α=22.5°或α=67.5°。
(2)解:6cos(α - 16°)=3$\sqrt{3}$,
两边同时除以6得:cos(α - 16°)=$\frac{\sqrt{3}}{2}$,
因为α为锐角,所以0°<α<90°,则-16°<α - 16°<74°,
所以α - 16°=30°,解得α=46°。
(1)解:因为α为锐角,所以0°<α<90°,则0°<2α<180°。
因为sin2α=$\frac{\sqrt{2}}{2}$,所以2α=45°或2α=135°,
解得α=22.5°或α=67.5°。
(2)解:6cos(α - 16°)=3$\sqrt{3}$,
两边同时除以6得:cos(α - 16°)=$\frac{\sqrt{3}}{2}$,
因为α为锐角,所以0°<α<90°,则-16°<α - 16°<74°,
所以α - 16°=30°,解得α=46°。
12. 如图,在$Rt\triangle ABC$中,已知$∠C= 90^{\circ }$,$D是边AC$上一点,$DE⊥AB于点E$,$DE:AE= 1:2$,求$\sin B$、$\cos B$、$\cot A$.
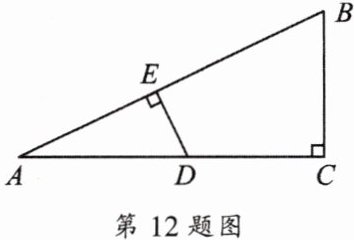

答案:
解:设$DE = k$,则$AE = 2k$。
在$Rt\triangle ADE$中,$\angle AED = 90^\circ$,
$\tan A = \frac{DE}{AE} = \frac{k}{2k} = \frac{1}{2}$,
$\cot A = \frac{1}{\tan A} = 2$。
设$BC = m$,$AC = 2m$(由$\tan A = \frac{BC}{AC} = \frac{1}{2}$得)。
在$Rt\triangle ABC$中,$\angle C = 90^\circ$,
$AB = \sqrt{AC^2 + BC^2} = \sqrt{(2m)^2 + m^2} = \sqrt{5}m$。
$\sin B = \frac{AC}{AB} = \frac{2m}{\sqrt{5}m} = \frac{2\sqrt{5}}{5}$,
$\cos B = \frac{BC}{AB} = \frac{m}{\sqrt{5}m} = \frac{\sqrt{5}}{5}$。
综上,$\sin B = \frac{2\sqrt{5}}{5}$,$\cos B = \frac{\sqrt{5}}{5}$,$\cot A = 2$。
在$Rt\triangle ADE$中,$\angle AED = 90^\circ$,
$\tan A = \frac{DE}{AE} = \frac{k}{2k} = \frac{1}{2}$,
$\cot A = \frac{1}{\tan A} = 2$。
设$BC = m$,$AC = 2m$(由$\tan A = \frac{BC}{AC} = \frac{1}{2}$得)。
在$Rt\triangle ABC$中,$\angle C = 90^\circ$,
$AB = \sqrt{AC^2 + BC^2} = \sqrt{(2m)^2 + m^2} = \sqrt{5}m$。
$\sin B = \frac{AC}{AB} = \frac{2m}{\sqrt{5}m} = \frac{2\sqrt{5}}{5}$,
$\cos B = \frac{BC}{AB} = \frac{m}{\sqrt{5}m} = \frac{\sqrt{5}}{5}$。
综上,$\sin B = \frac{2\sqrt{5}}{5}$,$\cos B = \frac{\sqrt{5}}{5}$,$\cot A = 2$。
13. 如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角$\alpha一般要满足50^{\circ }≤\alpha ≤75^{\circ }$. 现有一个长$6m$的梯子,问:使用这个梯子最高可以安全攀上多高的墙?(精确到$0.01m$)


答案:
解:由题意知,梯子长度为6m,梯子与地面所成角α满足50°≤α≤75°,墙高BC为梯子顶端到地面的距离,∠ACB=90°。
在Rt△ABC中,sinα=BC/AB,所以BC=AB·sinα。
因为AB=6m,且sinα随α增大而增大,当α=75°时,BC取得最大值。
则BC=6×sin75°≈6×0.9659≈5.7954≈5.80m。
答:使用这个梯子最高可以安全攀上约5.80m高的墙。
在Rt△ABC中,sinα=BC/AB,所以BC=AB·sinα。
因为AB=6m,且sinα随α增大而增大,当α=75°时,BC取得最大值。
则BC=6×sin75°≈6×0.9659≈5.7954≈5.80m。
答:使用这个梯子最高可以安全攀上约5.80m高的墙。
思维与拓展13
在$Rt\triangle ABC$中,已知$∠C= 90^{\circ }$,$∠BAC= 30^{\circ }$,延长$CA到点D$,使$AD= AB$,联结$BD$. 你能运用锐角三角比的知识求出$∠D$的正切和余切值吗?
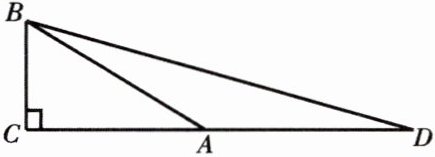
在$Rt\triangle ABC$中,已知$∠C= 90^{\circ }$,$∠BAC= 30^{\circ }$,延长$CA到点D$,使$AD= AB$,联结$BD$. 你能运用锐角三角比的知识求出$∠D$的正切和余切值吗?

答案:
【解析】:本题主要考察了直角三角形中锐角三角比的知识,包括正切和余切的计算。
首先,根据直角三角形的性质,在$Rt \bigtriangleup ABC$中,已知$\angle C= 90^{\circ }$,$\angle BAC= 30^{\circ }$,可以利用三角函数求出$BC$与$AB$的关系。
设$BC = a$,由于$\angle BAC= 30^{\circ }$,则$AB = 2a$(根据$30^{\circ }$角所对的直角边等于斜边的一半)。
利用勾股定理,可以求出$AC$的长度:
$AC = \sqrt{AB^2 - BC^2} = \sqrt{(2a)^2 - a^2} = \sqrt{3}a$,
由于$AD = AB = 2a$,所以$CD = AC + AD = \sqrt{3}a + 2a = (2 + \sqrt{3})a$,
在$Rt \bigtriangleup BCD$中,利用正切和余切的定义,可以求出$\angle D$的正切和余切值:
$\tan D = \frac{BC}{CD} = \frac{a}{(2 + \sqrt{3})a} = 2 - \sqrt{3}$,
$\cot D = \frac{CD}{BC} = \frac{(2 + \sqrt{3})a}{a} = 2 + \sqrt{3}$。
【答案】:$\tan D =2 - \sqrt{3}$;$\cot D =2 + \sqrt{3}$。
首先,根据直角三角形的性质,在$Rt \bigtriangleup ABC$中,已知$\angle C= 90^{\circ }$,$\angle BAC= 30^{\circ }$,可以利用三角函数求出$BC$与$AB$的关系。
设$BC = a$,由于$\angle BAC= 30^{\circ }$,则$AB = 2a$(根据$30^{\circ }$角所对的直角边等于斜边的一半)。
利用勾股定理,可以求出$AC$的长度:
$AC = \sqrt{AB^2 - BC^2} = \sqrt{(2a)^2 - a^2} = \sqrt{3}a$,
由于$AD = AB = 2a$,所以$CD = AC + AD = \sqrt{3}a + 2a = (2 + \sqrt{3})a$,
在$Rt \bigtriangleup BCD$中,利用正切和余切的定义,可以求出$\angle D$的正切和余切值:
$\tan D = \frac{BC}{CD} = \frac{a}{(2 + \sqrt{3})a} = 2 - \sqrt{3}$,
$\cot D = \frac{CD}{BC} = \frac{(2 + \sqrt{3})a}{a} = 2 + \sqrt{3}$。
【答案】:$\tan D =2 - \sqrt{3}$;$\cot D =2 + \sqrt{3}$。
查看更多完整答案,请扫码查看


