1. 如图,在$\triangle ABC$中,点$D$、$E分别在边AB$、$AC$上,且$DE// BC$。若$AD:DB = 3:1$,$AE = 6$,则$EC$等于(
A.2;
B.3;
C.4;
D.8.
A
)A.2;
B.3;
C.4;
D.8.
答案:
【解析】:本题可根据平行线分线段成比例定理来求解$EC$的长度。
已知$DE// BC$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
在$\triangle ABC$中,因为$DE// BC$,所以有$\frac{AD}{DB}=\frac{AE}{EC}$。
题目中已给出$AD:DB = 3:1$,即$\frac{AD}{DB}=\frac{3}{1}$,同时$AE = 6$,设$EC=x$,将已知条件代入到$\frac{AD}{DB}=\frac{AE}{EC}$中,可得$\frac{3}{1}=\frac{6}{x}$。
接下来求解上述方程:
根据比例的基本性质“两内项之积等于两外项之积”,可得$3x = 6×1$,即$3x = 6$。
两边同时除以$3$,解得$x = 2$,也就是$EC = 2$。
【答案】:A
已知$DE// BC$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
在$\triangle ABC$中,因为$DE// BC$,所以有$\frac{AD}{DB}=\frac{AE}{EC}$。
题目中已给出$AD:DB = 3:1$,即$\frac{AD}{DB}=\frac{3}{1}$,同时$AE = 6$,设$EC=x$,将已知条件代入到$\frac{AD}{DB}=\frac{AE}{EC}$中,可得$\frac{3}{1}=\frac{6}{x}$。
接下来求解上述方程:
根据比例的基本性质“两内项之积等于两外项之积”,可得$3x = 6×1$,即$3x = 6$。
两边同时除以$3$,解得$x = 2$,也就是$EC = 2$。
【答案】:A
2. 如图,在梯形$ABCD$中,$AD// BC$,$AC与BD相交于点O$,则下列说法正确的是(
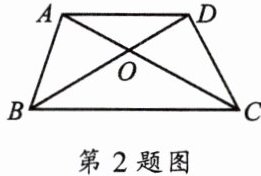
A.$\triangle AOD与\triangle BOC$的面积相等;
B.$\frac{OA}{OC}= \frac{OD}{OB}$;
C.$CO = 2AO$;
D.$BO = CO$.
B
)
A.$\triangle AOD与\triangle BOC$的面积相等;
B.$\frac{OA}{OC}= \frac{OD}{OB}$;
C.$CO = 2AO$;
D.$BO = CO$.
答案:
【解析】:本题可根据梯形的性质以及相似三角形的判定和性质来逐一分析选项。
选项A:判断$\triangle AOD$与$\triangle BOC$的面积是否相等
在梯形$ABCD$中,$AD// BC$,所以$\triangle AOD$与$\triangle BOC$相似(两角分别相等的两个三角形相似,因为$AD// BC$,所以$\angle OAD = \angle OCB$,$\angle ODA = \angle OBC$)。
但仅知道它们相似,并不能得出它们的面积相等,因为相似三角形面积比等于相似比的平方,而这里并没有给出相似比为$1$的条件,所以$\triangle AOD$与$\triangle BOC$的面积不一定相等,A选项错误。
选项B:判断$\frac{OA}{OC}= \frac{OD}{OB}$是否成立
由于$AD// BC$,根据平行线分线段成比例定理(三条平行线截两条直线,所得的对应线段成比例),可得$\triangle AOD\sim\triangle BOC$。
根据相似三角形的性质(相似三角形对应边成比例),可知$\frac{OA}{OC}=\frac{OD}{OB}$,B选项正确。
选项C:判断$CO = 2AO$是否成立
由前面分析可知$\triangle AOD\sim\triangle BOC$,但仅根据现有条件无法得出$\frac{OA}{OC}=\frac{1}{2}$,即不能得出$CO = 2AO$,C选项错误。
选项D:判断$BO = CO$是否成立
同样,仅由$AD// BC$得到$\triangle AOD\sim\triangle BOC$,不能得出$BO = CO$,D选项错误。
【答案】:B。
选项A:判断$\triangle AOD$与$\triangle BOC$的面积是否相等
在梯形$ABCD$中,$AD// BC$,所以$\triangle AOD$与$\triangle BOC$相似(两角分别相等的两个三角形相似,因为$AD// BC$,所以$\angle OAD = \angle OCB$,$\angle ODA = \angle OBC$)。
但仅知道它们相似,并不能得出它们的面积相等,因为相似三角形面积比等于相似比的平方,而这里并没有给出相似比为$1$的条件,所以$\triangle AOD$与$\triangle BOC$的面积不一定相等,A选项错误。
选项B:判断$\frac{OA}{OC}= \frac{OD}{OB}$是否成立
由于$AD// BC$,根据平行线分线段成比例定理(三条平行线截两条直线,所得的对应线段成比例),可得$\triangle AOD\sim\triangle BOC$。
根据相似三角形的性质(相似三角形对应边成比例),可知$\frac{OA}{OC}=\frac{OD}{OB}$,B选项正确。
选项C:判断$CO = 2AO$是否成立
由前面分析可知$\triangle AOD\sim\triangle BOC$,但仅根据现有条件无法得出$\frac{OA}{OC}=\frac{1}{2}$,即不能得出$CO = 2AO$,C选项错误。
选项D:判断$BO = CO$是否成立
同样,仅由$AD// BC$得到$\triangle AOD\sim\triangle BOC$,不能得出$BO = CO$,D选项错误。
【答案】:B。
3. 如图,在平行四边形$ABCD$中,已知$E是AD$上的一点,联结$CE并延长交BA的延长线于点F$,则下列结论错误的是(
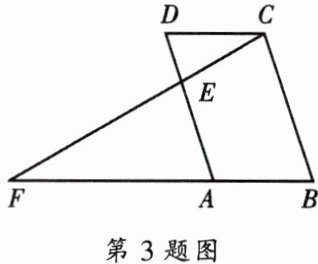
A.$\angle AEF= \angle DEC$;
B.$\frac{FA}{CD}= \frac{AE}{BC}$;
C.$\frac{FA}{AB}= \frac{FE}{EC}$;
D.$AB = DC$.
B
)
A.$\angle AEF= \angle DEC$;
B.$\frac{FA}{CD}= \frac{AE}{BC}$;
C.$\frac{FA}{AB}= \frac{FE}{EC}$;
D.$AB = DC$.
答案:
【解析】:首先,逐一分析每个选项:
A. $\angle AEF= \angle DEC$
由于$AB // CD$(因为$ABCD$是平行四边形),
根据平行线的性质,我们有$\angle F = \angle ECD$和$\angle FAE = \angle D$。
因此,$\triangle FAE \sim \triangle CDE$(AA相似)。
所以,$\angle AEF = \angle DEC$,选项A是正确的。
B. $\frac{FA}{CD}= \frac{AE}{BC}$
由于$\triangle FAE \sim \triangle CDE$,
我们有$\frac{FA}{CD} = \frac{FE}{EC}$。
但是,$\frac{FE}{EC} \neq \frac{AE}{BC}$,因为$AE$和$BC$不是相似三角形的对应边。
所以,选项B是错误的。
C. $\frac{FA}{AB}= \frac{FE}{EC}$
由于$\triangle FAE \sim \triangle CDE$,并且$AB = CD$(因为$ABCD$是平行四边形),
我们可以得到$\frac{FA}{CD} = \frac{FE}{EC}$,
进一步得到$\frac{FA}{AB} = \frac{FE}{EC}$。
所以,选项C是正确的。
D. $AB = DC$
这是平行四边形$ABCD$的一个基本性质,即对边相等。
所以,选项D是正确的。
综上所述,错误的选项是B。
【答案】:B。
A. $\angle AEF= \angle DEC$
由于$AB // CD$(因为$ABCD$是平行四边形),
根据平行线的性质,我们有$\angle F = \angle ECD$和$\angle FAE = \angle D$。
因此,$\triangle FAE \sim \triangle CDE$(AA相似)。
所以,$\angle AEF = \angle DEC$,选项A是正确的。
B. $\frac{FA}{CD}= \frac{AE}{BC}$
由于$\triangle FAE \sim \triangle CDE$,
我们有$\frac{FA}{CD} = \frac{FE}{EC}$。
但是,$\frac{FE}{EC} \neq \frac{AE}{BC}$,因为$AE$和$BC$不是相似三角形的对应边。
所以,选项B是错误的。
C. $\frac{FA}{AB}= \frac{FE}{EC}$
由于$\triangle FAE \sim \triangle CDE$,并且$AB = CD$(因为$ABCD$是平行四边形),
我们可以得到$\frac{FA}{CD} = \frac{FE}{EC}$,
进一步得到$\frac{FA}{AB} = \frac{FE}{EC}$。
所以,选项C是正确的。
D. $AB = DC$
这是平行四边形$ABCD$的一个基本性质,即对边相等。
所以,选项D是正确的。
综上所述,错误的选项是B。
【答案】:B。
4. 如图,已知点$D$、$E$、$F分别在\triangle ABC$的三边上,且$DE// BC$,$EF// AB$,则下列等式不成立的是(
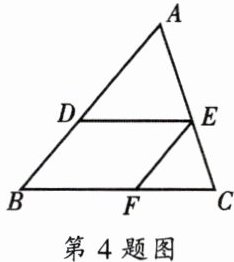
A.$\frac{AD}{AB}= \frac{AE}{AC}$;
B.$\frac{AE}{EC}= \frac{BF}{FC}$;
C.$\frac{AD}{BD}= \frac{BF}{FC}$;
D.$\frac{BD}{AD}= \frac{BF}{FC}$.
D
)
A.$\frac{AD}{AB}= \frac{AE}{AC}$;
B.$\frac{AE}{EC}= \frac{BF}{FC}$;
C.$\frac{AD}{BD}= \frac{BF}{FC}$;
D.$\frac{BD}{AD}= \frac{BF}{FC}$.
答案:
【解析】:本题可根据平行线分线段成比例定理以及相似三角形的性质来逐一分析选项。
已知$DE// BC$,$EF// AB$。
选项A:
因为$DE// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,可得$\frac{AD}{AB}=\frac{AE}{AC}$,所以该选项成立。
选项B:
由于$DE// BC$,$EF// AB$,则四边形$BDEF$是平行四边形,所以$DE = BF$。
又因为$DE// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,$\frac{AE}{EC}=\frac{AD}{DB}$;同时因为$EF// AB$,在$\triangle ABC$中,$\frac{AE}{EC}=\frac{BF}{FC}$,所以该选项成立。
选项C:
由$DE// BC$,根据平行线分线段成比例定理可得$\frac{AD}{BD}=\frac{AE}{EC}$;
因为$EF// AB$,所以$\frac{AE}{EC}=\frac{BF}{FC}$,那么$\frac{AD}{BD}=\frac{BF}{FC}$,该选项成立。
选项D:
由$DE// BC$,根据平行线分线段成比例定理可得$\frac{BD}{AD}=\frac{EC}{AE}$;
而$\frac{BF}{FC}=\frac{AE}{EC}$,所以$\frac{BD}{AD}\neq\frac{BF}{FC}$,该选项不成立。
【答案】:D。
已知$DE// BC$,$EF// AB$。
选项A:
因为$DE// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,可得$\frac{AD}{AB}=\frac{AE}{AC}$,所以该选项成立。
选项B:
由于$DE// BC$,$EF// AB$,则四边形$BDEF$是平行四边形,所以$DE = BF$。
又因为$DE// BC$,根据平行线分线段成比例定理,在$\triangle ABC$中,$\frac{AE}{EC}=\frac{AD}{DB}$;同时因为$EF// AB$,在$\triangle ABC$中,$\frac{AE}{EC}=\frac{BF}{FC}$,所以该选项成立。
选项C:
由$DE// BC$,根据平行线分线段成比例定理可得$\frac{AD}{BD}=\frac{AE}{EC}$;
因为$EF// AB$,所以$\frac{AE}{EC}=\frac{BF}{FC}$,那么$\frac{AD}{BD}=\frac{BF}{FC}$,该选项成立。
选项D:
由$DE// BC$,根据平行线分线段成比例定理可得$\frac{BD}{AD}=\frac{EC}{AE}$;
而$\frac{BF}{FC}=\frac{AE}{EC}$,所以$\frac{BD}{AD}\neq\frac{BF}{FC}$,该选项不成立。
【答案】:D。
5. 如图,已知$M$、$N分别是直角梯形ABCD两腰AD$、$CB$的中点,$DE\perp AB于点E$。将$\triangle ADE沿DE$翻折,若点$M与点N$恰好重合,则$AE:BE$等于(
A.$2:1$;
B.$1:2$;
C.$3:2$;
D.$2:3$.
A
)A.$2:1$;
B.$1:2$;
C.$3:2$;
D.$2:3$.
答案:
解:设 $ AE = x $,$ BE = y $,$ DE = h $。
由题意,$ DE \perp AB $,梯形 $ ABCD $ 为直角梯形,故 $ DEBC $ 为矩形,$ CD = BE = y $,$ BC = DE = h $。
$ M $、$ N $ 分别为 $ AD $、$ CB $ 中点,$ AD = \sqrt{AE^2 + DE^2} = \sqrt{x^2 + h^2} $,
则 $ M $ 坐标(以 $ A $ 为原点,$ AB $ 为 $ x $ 轴):$ \left( \frac{x}{2}, \frac{h}{2} \right) $,
$ N $ 坐标:$ \left( x + y, \frac{h}{2} \right) $。
翻折后 $ M $ 与 $ N $ 重合,$ M $ 关于 $ DE $($ x = x $)对称点为 $ N $,
对称点横坐标满足:$ x - \frac{x}{2} = x + y - x $,即 $ \frac{x}{2} = y $,
故 $ x:y = 2:1 $,即 $ AE:BE = 2:1 $。
答案:A。
由题意,$ DE \perp AB $,梯形 $ ABCD $ 为直角梯形,故 $ DEBC $ 为矩形,$ CD = BE = y $,$ BC = DE = h $。
$ M $、$ N $ 分别为 $ AD $、$ CB $ 中点,$ AD = \sqrt{AE^2 + DE^2} = \sqrt{x^2 + h^2} $,
则 $ M $ 坐标(以 $ A $ 为原点,$ AB $ 为 $ x $ 轴):$ \left( \frac{x}{2}, \frac{h}{2} \right) $,
$ N $ 坐标:$ \left( x + y, \frac{h}{2} \right) $。
翻折后 $ M $ 与 $ N $ 重合,$ M $ 关于 $ DE $($ x = x $)对称点为 $ N $,
对称点横坐标满足:$ x - \frac{x}{2} = x + y - x $,即 $ \frac{x}{2} = y $,
故 $ x:y = 2:1 $,即 $ AE:BE = 2:1 $。
答案:A。
6. 如图,已知$AB// CD$,若$OA = 3$,$AD = 7$,$OC = 5$,则$CB = $______.
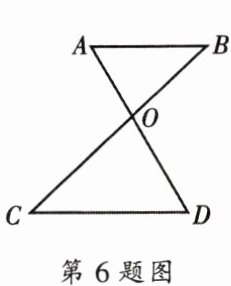

$\frac{35}{4}$
答案:
解:
∵AB//CD,
∴$\frac{OA}{OD}=\frac{OB}{OC}$。
∵OA=3,AD=7,
∴OD=AD - OA=7 - 3=4。
∵OC=5,
∴$\frac{3}{4}=\frac{OB}{5}$,解得OB=$\frac{15}{4}$。
∴CB=OB + OC=$\frac{15}{4}+5=\frac{35}{4}$。
$\frac{35}{4}$
∵AB//CD,
∴$\frac{OA}{OD}=\frac{OB}{OC}$。
∵OA=3,AD=7,
∴OD=AD - OA=7 - 3=4。
∵OC=5,
∴$\frac{3}{4}=\frac{OB}{5}$,解得OB=$\frac{15}{4}$。
∴CB=OB + OC=$\frac{15}{4}+5=\frac{35}{4}$。
$\frac{35}{4}$
7. 如图,在$\triangle ABC$中,已知$DE// BC$,$AB = 4$,$AC = 8$,$DB = AE$,则$AE = $
$\frac{8}{3}$
.
答案:
【解析】:本题可根据平行线分线段成比例定理列出关于$AE$的方程,进而求解$AE$的长度。
步骤一:根据平行线分线段成比例定理列出比例式
已知$DE// BC$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
可得$\frac{AD}{AB}=\frac{AE}{AC}$。
步骤二:用$AE$表示$AD$
因为$AB = 4$,$DB = AE$,所以$AD=AB - DB=4 - AE$。
步骤三:代入比例式求解$AE$
将$AD = 4 - AE$,$AB = 4$,$AC = 8$代入$\frac{AD}{AB}=\frac{AE}{AC}$中,得到$\frac{4 - AE}{4}=\frac{AE}{8}$。
交叉相乘可得:$8×(4 - AE)=4× AE$。
去括号:$32 - 8AE = 4AE$。
移项:$32 = 4AE + 8AE$。
合并同类项:$12AE = 32$。
系数化为$1$:$AE=\frac{32}{12}=\frac{8}{3}$。
【答案】:$\frac{8}{3}$
步骤一:根据平行线分线段成比例定理列出比例式
已知$DE// BC$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
可得$\frac{AD}{AB}=\frac{AE}{AC}$。
步骤二:用$AE$表示$AD$
因为$AB = 4$,$DB = AE$,所以$AD=AB - DB=4 - AE$。
步骤三:代入比例式求解$AE$
将$AD = 4 - AE$,$AB = 4$,$AC = 8$代入$\frac{AD}{AB}=\frac{AE}{AC}$中,得到$\frac{4 - AE}{4}=\frac{AE}{8}$。
交叉相乘可得:$8×(4 - AE)=4× AE$。
去括号:$32 - 8AE = 4AE$。
移项:$32 = 4AE + 8AE$。
合并同类项:$12AE = 32$。
系数化为$1$:$AE=\frac{32}{12}=\frac{8}{3}$。
【答案】:$\frac{8}{3}$
查看更多完整答案,请扫码查看


