《2025年中学生世界九年级数学上册沪教版五四制》

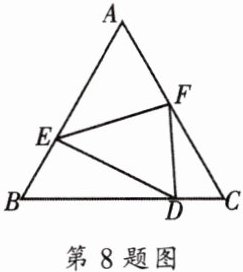
8. 如图,已知等边三角形ABC的边长为6,D是边BC上的一个动点,折叠$\triangle ABC$,使得点A恰好与边BC上的点D重合,折痕为EF(点E、F分别在边AB、AC上).
(1)当$AE:AF= 5:4$时,求BD的长；
(2)当以B、E、D为顶点的三角形与$\triangle DEF$相似时,求BD的长.

答案：
(1) 设 $ AE = 5k $, $ AF = 4k $, 则 $ BE = 6 - 5k $, $ CF = 6 - 4k $. 由折叠性质, 得 $ DE = AE = 5k $, $ DF = AF = 4k $. 设 $ BD = x $, 则 $ DC = 6 - x $.
在等边 $ \triangle ABC $ 中, $ \angle B = \angle C = 60^\circ $. 在 $ \triangle BDE $ 中, 由余弦定理: $ DE^2 = BE^2 + BD^2 - 2 \cdot BE \cdot BD \cdot \cos 60^\circ $, 即 $ (5k)^2 = (6 - 5k)^2 + x^2 - 2(6 - 5k)x \cdot \frac{1}{2} $, 化简得 $ 30k = x^2 - 6x + 36 - 5kx $. ①
在 $ \triangle CDF $ 中, 同理: $ DF^2 = CF^2 + CD^2 - 2 \cdot CF \cdot CD \cdot \cos 60^\circ $, 即 $ (4k)^2 = (6 - 4k)^2 + (6 - x)^2 - 2(6 - 4k)(6 - x) \cdot \frac{1}{2} $, 化简得 $ 24k = (6 - x)^2 - 6(6 - x) + 36 - 4k(6 - x) $. ②
联立①②, 消去 $ k $, 解得 $ x = 3 $, 即 $ BD = 3 $.
(2) 由折叠知 $ \angle EDF = \angle A = 60^\circ $, $ \angle B = 60^\circ $, 故 $ \angle EDF = \angle B $. 若 $ \triangle BED \sim \triangle DEF $, 则有两种情况:
情况1: $ \angle BED = \angle DEF $. 由折叠, $ \angle AEF = \angle DEF $, 故 $ \angle BED = \angle AEF $. 又 $ \angle AEF + \angle FEB = 180^\circ $, 则 $ \angle BED + \angle FEB = 180^\circ $, 即 $ E, F, D $ 共线, 矛盾, 舍去.
情况2: $ \angle BDE = \angle DEF $. 则 $ \triangle BED \sim \triangle DFE $, 故 $ \frac{BE}{DF} = \frac{BD}{DE} = \frac{DE}{EF} $. 设 $ BD = x $, $ AE = DE = m $, $ AF = DF = n $, 则 $ BE = 6 - m $. 由 $ \frac{BE}{DF} = \frac{BD}{DE} $, 得 $ \frac{6 - m}{n} = \frac{x}{m} $, 即 $ m(6 - m) = nx $. ③
由
(1)中 $ \triangle BDE $ 余弦定理: $ m^2 = (6 - m)^2 + x^2 - x(6 - m) $, 化简得 $ 12m = x^2 - 6x + 36 + mx $. ④
同理 $ \triangle AEF $ 中, $ EF^2 = m^2 + n^2 - mn $. 由相似比 $ \frac{DE}{EF} = \frac{BD}{DE} $, 得 $ EF = \frac{m^2}{x} $. 又 $ \angle EDF = 60^\circ $, 在 $ \triangle DEF $ 中, $ EF^2 = DE^2 + DF^2 - 2 \cdot DE \cdot DF \cdot \cos 60^\circ $, 即 $ \left( \frac{m^2}{x} \right)^2 = m^2 + n^2 - mn $. ⑤
联立③④⑤, 解得 $ x = 2 $ 或 $ x = 4 $.
综上, $ BD = 2 $ 或 $ 4 $.
答案:
(1) $ 3 $;
(2) $ 2 $ 或 $ 4 $.

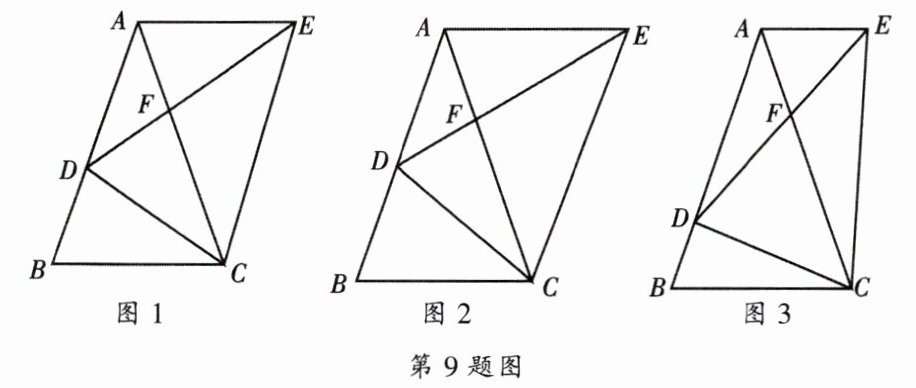
9. 如图,已知在$\triangle ABC$中,$AB= AC$,点D在边AB上,以DC为底边作等腰三角形EDC,腰DE与AC交于点F,联结AE.
(1)如图1,当$∠EFC= ∠ADC$时,求证：$AD^{2}= AF\cdot AB;$
(2)如图2,当$AF\cdot CF= DF\cdot EF$时,求证：$AE// BC;$
(3)如图3,当$AE// BC$时,求证：$\triangle EDC\backsim \triangle ABC.$

答案：
(1) 证明：
∵AB=AC，
∴∠B=∠ACB。
∵∠EFC=∠ADC，∠EFC=∠AFD（对顶角），
∴∠ADC=∠AFD。
∵∠A=∠A，
∴△ADF∽△ACD。
∴AD/AC=AF/AD，即AD²=AF·AC。
∵AB=AC，
∴AD²=AF·AB。
(2) 证明：
∵AF·CF=DF·EF，
∴AF/DF=EF/CF。
∵∠AFE=∠DFC（对顶角），
∴△AFE∽△DFC。
∴∠EAF=∠CDF。
∵AB=AC，
∴∠BAC=180°-2∠ACB。
∵ED=EC，
∴∠EDC=∠ECD，∠BAC=∠EAF+∠EAC=∠CDF+∠EAC。
∵∠CDF=∠B+∠BCD=∠ACB+∠BCD=∠ACD，
∴∠BAC=∠ACD+∠EAC。
∵∠BAC=180°-∠ADC-∠ACD，
∴180°-∠ADC-∠ACD=∠ACD+∠EAC，∠EAC=180°-∠ADC-2∠ACD。
∵∠ADC=180°-∠EDC=180°-∠ACD，
∴∠EAC=180°-(180°-∠ACD)-2∠ACD=-∠ACD。
∵∠EAC=∠ACB，
∴AE//BC。
(3) 证明：
∵AE//BC，
∴∠EAC=∠ACB。
∵AB=AC，
∴∠B=∠ACB=∠EAC。
∵∠AFC=∠B+∠FCD=∠EAC+∠AEF，
∴∠FCD=∠AEF。
∵∠AFE=∠DFC，
∴△AFE∽△CFD，AF/CF=EF/DF。
∵∠AFD=∠CFE，
∴△AFD∽△CFE，∠ADF=∠CEF。
∵ED=EC，
∴∠EDC=∠ECD=∠ADF+∠BDC=∠CEF+∠FED=∠CED。
∵∠B=∠EDC，∠ACB=∠ECD，
∴△EDC∽△ABC。

思维与拓展9
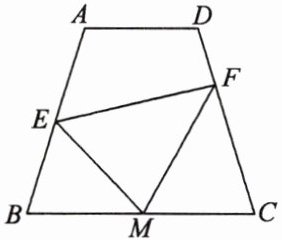
如图,在梯形ABCD中,$AD// BC$,$AB= CD= BC= 4$,$AD= 2$,点M为边BC的中点,以点M为顶点作$∠EMF= ∠B$,射线ME交边AB于点E,射线MF交边CD于点F,联结EF.
(1)指出图中所有与$\triangle BEM$相似的三角形,并加以证明；
(2)设$BE= x$,$CF= y$,求y关于x的函数解析式,并写出定义域；
(3)如果$\triangle BEM$是以BM为腰的等腰三角形,求EF的长.

答案： 1. （1）
与$\triangle BEM$相似的三角形有$\triangle CMF$和$\triangle MEF$。
证明$\triangle BEM\sim\triangle CMF$：
因为$AD// BC$，$AB = CD$，所以$\angle B=\angle C$。
又因为$\angle EMF+\angle FMC=\angle B + \angle BEM$，且$\angle EMF=\angle B$，所以$\angle BEM=\angle FMC$。
根据两角分别相等的两个三角形相似，可得$\triangle BEM\sim\triangle CMF$。
证明$\triangle BEM\sim\triangle MEF$：
由$\triangle BEM\sim\triangle CMF$，可得$\frac{BE}{CM}=\frac{EM}{FM}$。
因为$M$是$BC$中点，$BC = 4$，所以$BM = CM = 2$，则$\frac{BE}{BM}=\frac{EM}{FM}$。
又因为$\angle B=\angle EMF$，根据两边成比例且夹角相等的两个三角形相似，可得$\triangle BEM\sim\triangle MEF$。
2. （2）
因为$\triangle BEM\sim\triangle CMF$，所以$\frac{BE}{CM}=\frac{BM}{CF}$。
已知$BE = x$，$BM = CM = 2$，$CF = y$，则$\frac{x}{2}=\frac{2}{y}$，即$y=\frac{4}{x}$。
定义域：
当$E$与$A$重合时，$BE$最大。过$A$作$AH// DC$交$BC$于$H$，则$BH = BC - AD = 2$，$\triangle ABH$是等边三角形，$AB = 4$，所以$BE$最大为$4$；当$E$靠近$B$时，$BE\gt0$，所以定义域是$1\leqslant x\leqslant4$。
3. （3）EF长为3或4