《2025年中学生世界九年级数学上册沪教版五四制》

11. 已知$\triangle ABC \backsim \triangle A_1B_1C_1$,其相似比为$\frac{2}{3}$；$\triangle A_1B_1C_1 \backsim \triangle A_2B_2C_2$,其相似比为$\frac{5}{4}$,则$\triangle ABC与\triangle A_2B_2C_2$的对应角平分线长之比为$\frac{5}{6}$。

答案： 解：因为$\triangle ABC \backsim \triangle A_1B_1C_1$，相似比为$\frac{2}{3}$，所以$\triangle ABC$与$\triangle A_1B_1C_1$对应角平分线长之比为$\frac{2}{3}$。
因为$\triangle A_1B_1C_1 \backsim \triangle A_2B_2C_2$，相似比为$\frac{5}{4}$，所以$\triangle A_1B_1C_1$与$\triangle A_2B_2C_2$对应角平分线长之比为$\frac{5}{4}$。
设$\triangle ABC$、$\triangle A_1B_1C_1$、$\triangle A_2B_2C_2$的对应角平分线长分别为$d$、$d_1$、$d_2$，则$\frac{d}{d_1}=\frac{2}{3}$，$\frac{d_1}{d_2}=\frac{5}{4}$，所以$\frac{d}{d_2}=\frac{d}{d_1} \cdot \frac{d_1}{d_2}=\frac{2}{3} × \frac{5}{4}=\frac{5}{6}$。
故$\triangle ABC$与$\triangle A_2B_2C_2$的对应角平分线长之比为$\frac{5}{6}$。
答案：$\frac{5}{6}$

12. 如图,已知点$D在\triangle ABC的边BC$上,若$\angle DAC = \angle B$,且$BD = 5$,$AC = 6$,则$CD$的长为______4。

答案： 【解析】：
本题可根据相似三角形的判定定理和性质来求解$CD$的长。
步骤一：证明$\triangle CAD$与$\triangle CBA$相似
已知在$\triangle ABC$中，$\angle DAC = \angle B$，且$\angle C$是$\triangle CAD$与$\triangle CBA$的公共角，即$\angle C=\angle C$。
根据两角分别相等的两个三角形相似，可得$\triangle CAD\sim\triangle CBA$。
步骤二：根据相似三角形的性质列出比例式
因为相似三角形对应边成比例，由于$\triangle CAD\sim\triangle CBA$，所以$\frac{CD}{AC}=\frac{AC}{BC}$。
设$CD = x$，已知$BD = 5$，$AC = 6$，则$BC=BD + CD=5 + x$，代入上述比例式可得$\frac{x}{6}=\frac{6}{5 + x}$。
步骤三：求解上述方程
交叉相乘可得$x(5 + x)=36$，展开得到$x^{2}+5x - 36 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$（$a\neq0$），这里$a = 1$，$b = 5$，$c = -36$，可使用因式分解法求解，将方程$x^{2}+5x - 36 = 0$因式分解为$(x + 9)(x - 4)=0$。
则$x + 9 = 0$或$x - 4 = 0$，解得$x_{1}=-9$，$x_{2}=4$。
因为线段的长度不能为负，所以舍去$x_{1}=-9$，得到$x = 4$，即$CD = 4$。
【答案】：$4$

13. 在$\triangle ABC和\triangle DEF$中,已知$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} = \frac{3}{1}$,边$AB上的高为24$,求边$DE$上的高。

答案： 【解析】：
本题主要考察相似三角形的性质，即相似三角形对应高的比等于相似比。
已知两个三角形$\triangle ABC$和$\triangle DEF$是相似的，且它们的相似比为$\frac{3}{1}$。
根据相似三角形的性质，我们知道相似三角形对应高的比也等于相似比。
设边$DE$上的高为$h$，则有：
$\frac{AB \text{上的高}}{DE \text{上的高}} = \frac{3}{1}$
代入已知的$AB$上的高为$24$，我们得到：
$\frac{24}{h} = \frac{3}{1}$
解这个方程，我们可以得到$h$的值。
【答案】：
解：设边$DE$上的高为$h$。
根据相似三角形的性质，我们有：
$\frac{24}{h} = \frac{3}{1}$
解这个方程，我们得到：
$h = \frac{24}{3} = 8$
所以，边$DE$上的高为$8$。

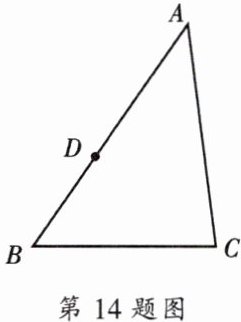
14. 如图,$\triangle ABC$中,已知$AB = 6$,$AC = 5$,$BC = 4$,点$D在边AB$上,且$AD = 4$,点$E在边AC$上。若以点$A$、$D$、$E为顶点的三角形与\triangle ABC$相似,试求$DE$的长。

答案： 【解析】：本题考查相似三角形的性质，利用相似三角形对应边成比例来求解$DE$的长，需要分情况讨论$\triangle ADE$与$\triangle ABC$的相似情况。
已知$\triangle ADE$与$\triangle ABC$相似，存在两种情况：
情况一：$\triangle ADE\sim\triangle ABC$，根据相似三角形对应边成比例，可得$\frac{DE}{BC}=\frac{AD}{AB}$。
情况二：$\triangle AED\sim\triangle ABC$，根据相似三角形对应边成比例，可得$\frac{DE}{BC}=\frac{AE}{AC}$，同时还需要根据$AE$与$AC$的关系进一步求解$DE$。
【答案】：解：
情况一：当$\triangle ADE\sim\triangle ABC$时，
根据相似三角形对应边成比例，可得$\frac{DE}{BC}=\frac{AD}{AB}$。
已知$AB = 6$，$AD = 4$，$BC = 4$，将其代入上式可得：
$\frac{DE}{4}=\frac{4}{6}$
$DE=\frac{4×4}{6}=\frac{8}{3}$
情况二：当$\triangle AED\sim\triangle ABC$时，
根据相似三角形对应边成比例，可得$\frac{DE}{BC}=\frac{AD}{AC}$。
已知$AC = 5$，$AD = 4$，$BC = 4$，将其代入上式可得：
$\frac{DE}{4}=\frac{4}{5}$
$DE=\frac{4×4}{5}=\frac{16}{5}$
综上，$DE$的长为$\frac{8}{3}$或$\frac{16}{5}$。

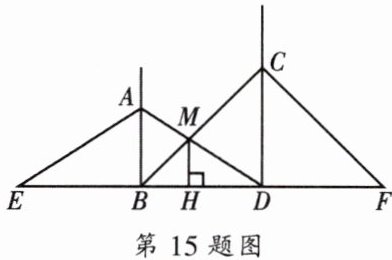
15. 如图,$AB和CD$两根电线杆,分别在高$10m的A处和15m的C$处用钢索将两杆固定,求钢索$AD与钢索BC的交点M离地面的高度MH$。

答案： 解：设MH = h，BD = x，BH = m，HD = n，则m + n = x。
因为AB⊥EF，CD⊥EF，MH⊥EF，所以AB//MH//CD。
所以△MHD∽△ABD，△MHB∽△CDB。
由△MHD∽△ABD，得$\frac{MH}{AB} = \frac{HD}{BD}$，即$\frac{h}{10} = \frac{n}{x}$ ①。
由△MHB∽△CDB，得$\frac{MH}{CD} = \frac{BH}{BD}$，即$\frac{h}{15} = \frac{m}{x}$ ②。
① + ②，得$\frac{h}{10} + \frac{h}{15} = \frac{m + n}{x} = 1$。
解得$h = 6$。
答：钢索AD与钢索BC的交点M离地面的高度MH为6m。