《2025年中学生世界九年级数学上册沪教版五四制》

13. 如图,已知$AD$、$BE是\triangle ABC$的两条高线.
求证：$\frac{BC}{AC}= \frac{BE}{AD}$.

答案： 【解析】：本题可根据三角形面积公式来证明$\frac{BC}{AC}= \frac{BE}{AD}$。
三角形的面积公式为$S = \frac{1}{2}×底×高$。
对于$\triangle ABC$，以$BC$为底时，$AD$是高，则其面积$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD$；
以$AC$为底时，$BE$是高，则其面积$S_{\triangle ABC}=\frac{1}{2}AC\cdot BE$。
由于$\triangle ABC$的面积是固定的，所以$\frac{1}{2}BC\cdot AD=\frac{1}{2}AC\cdot BE$，
等式两边同时除以$\frac{1}{2}AC\cdot AD$，即可得到$\frac{BC}{AC}= \frac{BE}{AD}$。
【答案】：证明：
∵$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD$，$S_{\triangle ABC}=\frac{1}{2}AC\cdot BE$
∴$\frac{1}{2}BC\cdot AD=\frac{1}{2}AC\cdot BE$
∴$\frac{BC}{AC}= \frac{BE}{AD}$

14. 已知点$C是线段AB$的黄金分割点,$BC = AC + 2$,求线段$AC$的长.

答案： 【解析】：
本题主要考查黄金分割点的性质。
设线段$AC$的长度为$x$，根据题意有$BC = x + 2$。
由于点C是线段AB的黄金分割点，根据黄金分割的定义，有$\frac{AC}{BC} = \frac{\sqrt{5} - 1}{2}$。
代入$AC$和$BC$的表达式，得到方程：$\frac{x}{x + 2} = \frac{\sqrt{5} - 1}{2}$。
接下来我们解这个方程：
首先，将方程两边同时乘以$2(x + 2)$，得到：
$2x = (\sqrt{5} - 1)(x + 2)$
展开并整理得：
$2x = \sqrt{5}x + 2\sqrt{5} - x - 2$
将所有含$x$的项移到方程的一边，常数项移到另一边，得：
$2x - \sqrt{5}x + x = 2\sqrt{5} - 2$
合并同类项，得：
$(3 - \sqrt{5})x = 2(\sqrt{5} - 1)$
最后，解出$x$，即：
$x = \frac{2(\sqrt{5} - 1)}{3 - \sqrt{5}}$
为了消去分母中的根号，我们可以用共轭式的方法，即乘以$\frac{3 + \sqrt{5}}{3 + \sqrt{5}}$，得：
$x = \frac{2(\sqrt{5} - 1)(3 + \sqrt{5})}{(3 - \sqrt{5})(3 + \sqrt{5})}$
展开并简化得：
$x = \frac{2(3\sqrt{5} + 5 - 3 - \sqrt{5})}{9 - 5}$
$x = \frac{2(2\sqrt{5} + 2)}{4}$
$x = \frac{4\sqrt{5} + 4}{4}$
$x = \sqrt{5} + 1$
【答案】：
$AC = \sqrt{5} + 1$

15. 如图,在梯形$ABCD$中,已知$AD// BC$.
(1)求证：$S_{\triangle AOB}= S_{\triangle COD}$；
(2)求证：$\frac{AO}{AC}= \frac{DO}{DB}$.

答案： 【解析】：
(1) 本题考查梯形中位线的性质以及三角形面积的计算。由于$AD// BC$，所以梯形$ABCD$是梯形，根据梯形的性质，我们可以得到$\triangle ADB$和$\triangle ACB$的面积相等，即$S_{\triangle ADB} = S_{\triangle ACB}$。由于$\triangle AOB$是这两个三角形的公共部分，所以$S_{\triangle AOB} = S_{\triangle ADB} - S_{\triangle AOD} = S_{\triangle ACB} - S_{\triangle AOD} = S_{\triangle COD}$（等量代换）。也可以利用$\triangle ADO$和$\triangle CBO$相似，得到面积比等于相似比的平方，再通过等量代换得到$S_{\triangle AOB} = S_{\triangle COD}$。
(2) 本题考查比例线段的性质。由于$AD// BC$，根据平行线分线段成比例定理，我们有$\frac{AO}{OC} = \frac{DO}{OB}$。通过交叉相乘，我们得到$AO × OB = DO × OC$。再根据比例的性质，我们可以得到$\frac{AO}{AO + OC} = \frac{DO}{DO + OB}$，即$\frac{AO}{AC} = \frac{DO}{DB}$。
【答案】：
(1) 证明：
∵$S_{\triangle ADB} = \frac{1}{2}AD × 高$，$S_{\triangle ACB} = \frac{1}{2}BC × 同一高$，
∵$AD// BC$，所以高相同，
∴$S_{\triangle ADB} = S_{\triangle ACB}$，
∵$S_{\triangle AOB} = S_{\triangle ADB} - S_{\triangle AOD}$，$S_{\triangle COD} = S_{\triangle ACB} - S_{\triangle AOD}$，
∴$S_{\triangle AOB} = S_{\triangle COD}$。
(2) 证明：
∵$AD// BC$，
∴$\frac{AO}{OC} = \frac{DO}{OB}$，
∴$AO × OB = DO × OC$，
∴$\frac{AO}{AO + OC} = \frac{DO}{DO + OB}$，
即$\frac{AO}{AC} = \frac{DO}{DB}$。

思维与拓展3
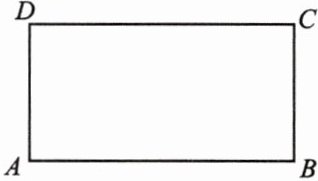
若一个矩形的短边与长边的比值是$\frac{\sqrt{5}-1}{2}$(黄金比),就称这样的矩形是黄金矩形.
(1)操作：请你在如图所示的黄金矩形$ABCD(AB ＞ AD)$内,以短边$AD为一边作正方形AEFD$；
(2)探究：在(1)中的四边形$EBCF$是不是黄金矩形.请说明理由.

答案： 【解析】：本题主要考查对黄金矩形的理解和证明。首先，我们需要明确黄金矩形的定义，即短边与长边的比值为黄金比$\frac{\sqrt{5}-1}{2}$。接着，我们通过作正方形AEFD，得到新的四边形EBCF。为了证明四边形EBCF是黄金矩形，我们需要计算其短边与长边的比值，并验证其是否等于黄金比。
(1)根据题目要求，我们可以在黄金矩形$ABCD$内，以短边$AD$为一边作正方形$AEFD$。
(2)为了证明四边形$EBCF$是黄金矩形，我们可以按照以下步骤进行：
第一步，由于四边形$AEFD$是正方形，所以$\angle AEF = 90^\circ$，$AE=AD$，又因为矩形$ABCD$中$\angle B=\angle C= \angle D= \angle A=90^\circ$，所以$EF// CD$，即$\angle B=\angle C= \angle BEF=90^\circ$，根据矩形的判定：有三个角是直角的四边形是矩形，所以四边形$EBCF$是矩形。
第二步，设$AD=x$，由于矩形$ABCD$是黄金矩形，根据黄金矩形的定义，我们有$\frac{AD}{AB}=\frac{\sqrt{5}-1}{2}$，即$AB=\frac{2x}{\sqrt{5}-1}$，为了化简这个表达式，我们可以使用有理化分母的方法，得到：
$AB=\frac{2x}{\sqrt{5}-1}=\frac{2x(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}=\frac{2x(\sqrt{5}+1)}{5-1}=\frac{x(\sqrt{5}+1)}{2}$。
第三步，计算$BE$的长度，$BE=AB-AE=\frac{x(\sqrt{5}+1)}{2}-x=\frac{x(\sqrt{5}-1)}{2}$。
第四步，验证四边形$EBCF$是否为黄金矩形，即验证$\frac{BE}{BC}$是否等于黄金比。由于$BC=AD=x$，我们有：
$\frac{BE}{BC}=\frac{\frac{x(\sqrt{5}-1)}{2}}{x}=\frac{\sqrt{5}-1}{2}$，这恰好是黄金比。
所以，我们可以得出结论：四边形$EBCF$是黄金矩形。
【答案】：
(1)见解析；
(2)四边形$EBCF$是黄金矩形，理由见解析。