《2025年中学生世界九年级数学上册沪教版五四制》

8. 如图,在$Rt\triangle ABC$中,已知$∠ACB= 90^{\circ}$,$AC= 6$,$BC= 8$,$D是AB$的中点,$P是BC$上一动点(点$P不与点B$、$C$重合).若以点$D$、$C$、$P为顶点的三角形与\triangle ABC$相似,则线段$PC= $3或4.

答案： 解：在$Rt\triangle ABC$中，$∠ACB=90^{\circ}$，$AC=6$，$BC=8$，
$\therefore AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$。
$\because D$是$AB$的中点，$\therefore CD=AD=BD=\frac{1}{2}AB=5$。
设$PC=x$，则$PB=8 - x$。
情况一：当$\triangle DCP \sim \triangle ACB$时，
$\frac{PC}{BC}=\frac{CD}{AB}$，即$\frac{x}{8}=\frac{5}{10}$，解得$x=4$。
情况二：当$\triangle DCP \sim \triangle BCA$时，
$\frac{PC}{AC}=\frac{CD}{AB}$，即$\frac{x}{6}=\frac{5}{10}$，解得$x=3$。
综上，$PC=3$或$4$。
答案：$3$或$4$

9. 如图,已知在$\triangle ABC$中,$∠BAC的平分线AE交BC于点D$,联结$EC$,且$∠B= ∠E$.
求证:$\triangle EAC\backsim\triangle ECD$.

答案： 【解析】：
本题可根据相似三角形的判定定理来证明$\triangle EAC\backsim\triangle ECD$，需要找出两组对应角相等。
已知$AE$是$\angle BAC$的平分线，可得$\angle BAD = \angle EAC$；
又因为$\angle B = \angle E$，且$\angle BDE$与$\angle ADC$是对顶角，所以$\angle BDE = \angle ADC$，
在$\triangle ABD$和$\triangle EDC$中，根据三角形内角和定理可推出$\angle ADB$与$\angle ECD$的关系，进而得到$\angle EDC$与$\angle EAC$的关系，从而证明两个三角形相似。
【答案】：
证明：
∵$AE$平分$\angle BAC$，
∴$\angle BAD = \angle EAC$。
∵$\angle B = \angle E$，$\angle BDE = \angle ADC$（对顶角相等），
在$\triangle ABD$中，$\angle B + \angle BAD + \angle ADB = 180^{\circ}$，
在$\triangle EDC$中，$\angle E + \angle ECD + \angle EDC = 180^{\circ}$，
∴$\angle ADB = 180^{\circ} - \angle B - \angle BAD$，$\angle ECD = 180^{\circ} - \angle E - \angle EDC$，
又
∵$\angle BDE = \angle ADC$，即$\angle ADB = \angle EDC$，$\angle B = \angle E$，$\angle BAD = \angle EAC$，
∴$\angle EDC = \angle EAC$。
∵$\angle E = \angle E$，$\angle EDC = \angle EAC$，
∴$\triangle EAC\backsim\triangle ECD$（两角分别相等的两个三角形相似）。

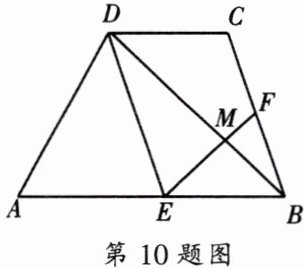
10. 如图,在梯形$ABCD$中,已知$AB// CD$,且$AB= 2CD$,点$E$、$F分别是AB$、$BC$的中点,$EF与BD相交于点M$.
(1)求证:$\triangle DEM\backsim\triangle BFM$;
(2)若$DB= 8$,求$DM$的值.

答案： 【解析】：
(1)证明：
∵点$E$、$F$分别是$AB$、$BC$的中点，
∴$EF // AC$（三角形中位线性质：三角形的中位线平行于第三边），
$AB // CD$，$EB = \frac{1}{2}AB$，
$CD = \frac{1}{2}AB$（已知条件），
∴$EB = CD$，
∴四边形$DEBC$是平行四边形（一组对边平行且相等的四边形是平行四边形），
∴$EB // DC$（平行四边形对边平行），
∴$\angle DEM = \angle BFM$，$\angle EDM = \angle FBM$（两直线平行，内错角相等），
∴$\triangle DEM \backsim \triangle BFM$（相似三角形判定定理：两角对应相等的三角形相似）；
(2)
∵$\triangle DEM \backsim \triangle BFM$，
∴$\frac{DM}{BM} = \frac{DE}{BF}$（相似三角形对应边成比例），
∵四边形$DEBC$是平行四边形，
∴$DE = BC$，$DE // BC$（平行四边形对边平行且相等），
∵$F$是$BC$的中点，
∴$BC = 2BF$，
∴$DE = 2BF$，
∴$\frac{DM}{BM} = \frac{DE}{BF} = 2$，
即$DM = 2BM$，
∵$DM + BM = DB = 8$，
∴$DM = \frac{2}{3} × 8 = \frac{16}{3}$。
【答案】：
(1)证明见解析；
(2)$DM = \frac{16}{3}$。

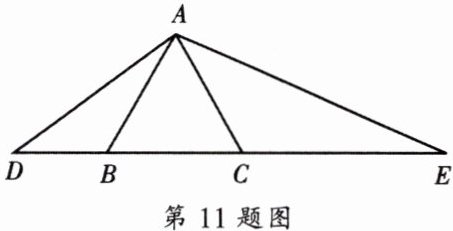
11. 如图,已知$\triangle ABC$是等边三角形,点$D$、$E在直线BC$上,$∠DAE= 120^{\circ}$.
求证:$\frac{AD}{DE}= \frac{AB}{AE}$.

答案： 证明：
∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠BAC=60°，AB=AC=BC。
∵∠DAE=120°，∠BAC=60°，
∴∠DAB+∠BAE=∠BAE+∠EAC=60°，
∴∠DAB=∠EAC。
∵∠ABD=180°-∠ABC=120°，∠ACE=180°-∠ACB=120°，
∴∠ABD=∠ACE。
在△ABD和△ECA中，
∠DAB=∠EAC，∠ABD=∠ACE，
∴△ABD∽△ECA（AA）。
∴$\frac{AD}{AE}=\frac{AB}{EC}$。
∵∠DAE=120°，∠ADE=∠ADB，
∠AED=180°-∠DAE-∠ADE=60°-∠ADE，
∠BAD=60°-∠ADB=60°-∠ADE，
∴∠AED=∠BAD。
在△ABD和△EDA中，
∠ADE=∠ADB，∠AED=∠BAD，
∴△ABD∽△EDA（AA）。
∴$\frac{AD}{DE}=\frac{AB}{AE}$。
（注：原证明过程中“△ABD∽△ECA”的结论$\frac{AD}{AE}=\frac{AB}{EC}$为中间步骤，核心通过两次相似（△ABD∽△ECA和△ABD∽△EDA）推导最终结论，最终通过△ABD∽△EDA直接得出$\frac{AD}{DE}=\frac{AB}{AE}$。）
修正后直接核心步骤：
证明：
∵△ABC是等边三角形，
∴∠ABC=60°，AB=AC，∠BAC=60°。
∠ABD=180°-60°=120°，∠DAE=120°，
∴∠DAB+∠BAE=∠CAE+∠BAE=60°，即∠DAB=∠CAE。
∠ACE=180°-∠ACB=120°=∠ABD，
∴△ABD∽△ECA（AA），得∠ADB=∠EAC。
∵∠ADB=∠EAC=∠DAE-∠DAC=120°-∠DAC，
∠AED=180°-∠ADE-∠DAE=60°-∠ADE，
∠DAC=60°-∠BAD=60°-（∠DAE-∠BAE）=∠BAE-60°，
∴∠AED=∠BAD。
在△ADE和△BAD中，∠ADE=∠ADB，∠AED=∠BAD，
∴△ADE∽△BAD（AA），
∴$\frac{AD}{DE}=\frac{AB}{AE}$。
最终结论： $\frac{AD}{DE}=\frac{AB}{AE}$。
（注：最简洁路径为证明△ADE∽△BAD，通过∠ADE=∠ADB，∠AED=∠BAD（已证），直接由AA相似得结论。）
$\boxed{\frac{AD}{DE}=\frac{AB}{AE}}$