《2025年中学生世界九年级数学上册沪教版五四制》

1. 两个相似三角形对应中线的比为$4:5$,周长之和为36,那么较大三角形的周长是 (B)
A.16；
B.20；
C.24；
D.12.

答案： 【解析】：
本题考查相似三角形的性质。
根据相似三角形的性质，如果两个相似三角形的对应边（或对应中线）之比为 $k$，
则它们的周长之比也为 $k$。
题目给出两个相似三角形对应中线的比为 $4:5$，周长之和为$36$。
设较小三角形的周长为 $4x$，较大三角形的周长为 $5x$。
根据周长之和，可以列出方程：
$4x + 5x = 36$，
解这个方程，得到 ：
$x = 4$，
将 $x = 4$ 代入 $5x$，得到较大三角形的周长为 $5 × 4 = 20$。
【答案】：
B. $20$。

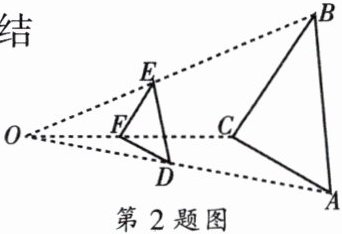
2. 如图,按如下方法,将$\triangle ABC的三边缩小到原来的\frac {1}{2}$,任取一点O,联结AO、BO、CO,并取它们的中点D、E、F,得$\triangle DEF$,则下列说法正确的是( C )
①$\triangle ABC与\triangle DEF$是相似图形；
②$\triangle ABC与\triangle DEF的周长之比为1:2;$
③$\triangle ABC与\triangle DEF的面积之比为4:1.$

A.①、②；
B.②、③；
C.①、③；
D.①、②、③.

答案： 【解析】：本题可根据相似三角形的判定定理和性质来逐一分析各说法。
判断①$\triangle ABC$与$\triangle DEF$是否为相似图形：
已知$D$、$E$、$F$分别是$AO$、$BO$、$CO$的中点，根据三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。
在$\triangle ABC$中，$DE$是$\triangle OAB$的中位线，则$DE// AB$，且$DE = \frac{1}{2}AB$；同理$EF// BC$，且$EF = \frac{1}{2}BC$；$DF// AC$，且$DF = \frac{1}{2}AC$。
因为$\angle EDF=\angle BAC$（两直线平行，同位角相等），$\angle DEF=\angle ABC$，$\angle DFE=\angle ACB$，所以$\triangle DEF\sim\triangle ABC$，即$\triangle ABC$与$\triangle DEF$是相似图形，故①正确。
判断②$\triangle ABC$与$\triangle DEF$的周长之比是否为$1:2$：
由相似三角形的性质：相似三角形周长的比等于相似比。
因为$\triangle DEF\sim\triangle ABC$，且$DE = \frac{1}{2}AB$，$EF = \frac{1}{2}BC$，$DF = \frac{1}{2}AC$，所以$\triangle ABC$与$\triangle DEF$的相似比为$2:1$，那么它们的周长之比也为$2:1$，而不是$1:2$，故②错误。
判断③$\triangle ABC$与$\triangle DEF$的面积之比是否为$4:1$：
根据相似三角形的性质：相似三角形面积的比等于相似比的平方。
由于$\triangle ABC$与$\triangle DEF$的相似比为$2:1$，所以它们的面积之比为$2^2:1^2 = 4:1$，故③正确。
综上，①③正确，答案选C。
【答案】：C

3. 已知梯形ABCD的对角线交于点O,$AD// BC$,有以下四个结论：
①$\triangle AOB\backsim \triangle COD$；②$\triangle AOD\backsim \triangle BOC$；③$S_{\triangle COD}:S_{\triangle AOD}= BC:AD$；④$S_{\triangle COD}= S_{\triangle AOB}.$
其中正确的结论有 (B)
A.1个；
B.2个；
C.3个；
D.4个.

答案： 解：
①
∵AD//BC，
∴∠OAD=∠OCB，∠ODA=∠OBC，
∴△AOD∽△COB（AA），则△AOB与△COD不相似，①错误；
② 由①知△AOD∽△COB，②正确；
③
∵△COD与△AOD等高，
∴S△COD:S△AOD=OC:OA，又△AOD∽△COB，得OC:OA=BC:AD，
∴S△COD:S△AOD=BC:AD，③正确；
④ 设AD=a，BC=b，相似比为a:b，S△AOD:S△COB=a²:b²，S△AOB=S△COD，若a≠b，则S△COD≠S△AOB，④错误。
正确结论为②③，共2个。
答案：B

4. 如图,已知在$\triangle ABC$中,点D、E分别在边AB、AC上,$DE// BC$,$DE= 2cm$,$BC= 5cm$,四边形BCED的周长为16cm,则$\triangle ADE$的周长为____6cm.

答案： 1. 首先，因为$DE// BC$，所以$\triangle ADE\sim\triangle ABC$。
根据相似三角形的性质，相似三角形的周长比等于相似比。相似比$k = \frac{DE}{BC}$，已知$DE = 2cm$，$BC = 5cm$，则$k=\frac{DE}{BC}=\frac{2}{5}$。
设$\triangle ADE$的周长为$C_{1}$，$\triangle ABC$的周长为$C_{2}$，则$\frac{C_{1}}{C_{2}}=\frac{DE}{BC}=\frac{2}{5}$，即$C_{2}=\frac{5}{2}C_{1}$。
2. 然后，分析周长关系：
因为$C_{2}=C_{1}+C_{四边形BCED}-DE - BC$（$C_{四边形BCED}=BD + BC+CE + DE$，$C_{2}=AD + BD+BC + CE+AE$，$C_{1}=AD + AE+DE$）。
已知$C_{四边形BCED}=16cm$，$DE = 2cm$，$BC = 5cm$，所以$C_{2}=C_{1}+16-(2 + 5)$。
3. 接着，将$C_{2}=\frac{5}{2}C_{1}$代入$C_{2}=C_{1}+16-(2 + 5)$：
把$C_{2}=\frac{5}{2}C_{1}$代入$C_{2}=C_{1}+9$中，得到$\frac{5}{2}C_{1}=C_{1}+9$。
移项可得：$\frac{5}{2}C_{1}-C_{1}=9$。
通分：$\frac{5C_{1}-2C_{1}}{2}=9$，即$\frac{3C_{1}}{2}=9$。
两边同时乘以$\frac{2}{3}$，解得$C_{1}=6$。
所以$\triangle ADE$的周长为$6cm$。

5. 已知四边形ABCD是矩形,$AB= \sqrt {3}$,对角线AC的中垂线与直线BC交于点M,与直线AD交于点N. 若$\frac {DN}{CM}= \frac {1}{2}$,则边AD的长为3.

答案： 1. 设$AD = x$，$DN = y$，则$CM = 2y$：
因为四边形$ABCD$是矩形，所以$AD// BC$，$\angle B=\angle D = 90^{\circ}$，$AD = BC=x$，$AB = CD=\sqrt{3}$。
由于$MN$是$AC$的中垂线，所以$AN = CN$，$AM = CM$。
则$AN=AD - DN=x - y$，$BM=BC - CM=x - 2y$，$AM = CM = 2y$。
2. 在$Rt\triangle ABM$中，根据勾股定理$AB^{2}+BM^{2}=AM^{2}$：
已知$AB = \sqrt{3}$，$BM=x - 2y$，$AM = 2y$，代入勾股定理公式$a^{2}+b^{2}=c^{2}$（这里$a = AB$，$b = BM$，$c = AM$）可得：
$(\sqrt{3})^{2}+(x - 2y)^{2}=(2y)^{2}$。
展开式子：$3+x^{2}-4xy + 4y^{2}=4y^{2}$。
化简得：$x^{2}-4xy+3 = 0$。
又因为$CN=AN=x - y$，在$Rt\triangle CDN$中，根据勾股定理$CD^{2}+DN^{2}=CN^{2}$，$CD=\sqrt{3}$，$DN = y$，$CN=x - y$，则$(\sqrt{3})^{2}+y^{2}=(x - y)^{2}$。
展开式子：$3 + y^{2}=x^{2}-2xy + y^{2}$。
化简得：$x^{2}-2xy-3 = 0$。
3. 联立方程组：
由$\begin{cases}x^{2}-4xy + 3 = 0\\x^{2}-2xy-3 = 0\end{cases}$，用第二个方程$x^{2}-2xy-3 = 0$减去第一个方程$x^{2}-4xy + 3 = 0$：
$(x^{2}-2xy-3)-(x^{2}-4xy + 3)=0$。
去括号得：$x^{2}-2xy-3 - x^{2}+4xy - 3 = 0$。
合并同类项得：$2xy-6 = 0$，即$xy = 3$，$y=\frac{3}{x}$。
将$y=\frac{3}{x}$代入$x^{2}-2xy-3 = 0$中，得到$x^{2}-2x×\frac{3}{x}-3 = 0$。
化简：$x^{2}-6 - 3 = 0$。
即$x^{2}=9$。
因为$x\gt0$（边长大于$0$），所以$x = 3$。
所以边$AD$的长为$3$。

6. 在$\triangle ABC$中,已知$∠ACB= 90^{\circ }$,$CD⊥AB$,垂足是D,$\frac {AD}{AC}= \frac {3}{5}$,$\triangle ABC$的周长是25,则$\triangle ACD$的周长是____18.

答案： 解：设$AD = 3k$，则$AC = 5k$。
在$Rt\triangle ACD$中，$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(5k)^{2}-(3k)^{2}} = 4k$。
因为$\angle ACB = 90^{\circ}$，$CD\perp AB$，所以$\triangle ACD\sim\triangle ABC$。
相似比为$\frac{AC}{AB}=\frac{AD}{AC}=\frac{3}{5}$，即$\frac{5k}{AB}=\frac{3}{5}$，解得$AB=\frac{25k}{3}$。
$\triangle ABC$周长为$AB + BC + AC=\frac{25k}{3}+BC + 5k = 25$，由相似比$\frac{BC}{CD}=\frac{5}{3}$得$BC=\frac{5}{3}CD=\frac{20k}{3}$。
代入周长：$\frac{25k}{3}+\frac{20k}{3}+5k = 25$，解得$k=\frac{3}{2}$。
$\triangle ACD$周长为$AD + CD + AC=3k + 4k + 5k = 12k=12×\frac{3}{2}=18$。
18

7. 如图,在$\triangle ABC$中,$AB= 10$,$AC= 15$,点D、E分别在AB、AC上,使$∠AED= ∠B$,$S_{\triangle ADE}= 4$,$S_{\triangle ABC}= 25$.求AD、AE的长.

答案： 【解析】：
本题可根据相似三角形的判定定理得出$\triangle ADE$与$\triangle ABC$相似，再利用相似三角形的性质列出关于$AD$、$AE$的方程，进而求解$AD$、$AE$的长。
步骤一：证明$\triangle ADE$与$\triangle ABC$相似
已知$\angle AED = \angle B$，且$\angle A$是$\triangle ADE$与$\triangle ABC$的公共角，即$\angle A=\angle A$。
根据两角分别相等的两个三角形相似，可得$\triangle ADE\sim\triangle ABC$。
步骤二：根据相似三角形的性质列出比例式
相似三角形面积比等于相似比的平方，因为$\triangle ADE\sim\triangle ABC$，所以$\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{AD}{AB})^2 = (\frac{AE}{AC})^2$。
已知$S_{\triangle ADE} = 4$，$S_{\triangle ABC} = 25$，$AB = 10$，$AC = 15$，代入上式可得$(\frac{AD}{10})^2 = \frac{4}{25}$，$(\frac{AE}{15})^2 = \frac{4}{25}$。
步骤三：求解$AD$、$AE$的长
对$(\frac{AD}{10})^2 = \frac{4}{25}$求解：
等式两边同时开平方可得$\frac{AD}{10}=\pm\sqrt{\frac{4}{25}}=\pm\frac{2}{5}$。
因为$AD$为线段长度，大于$0$，所以舍去$\frac{AD}{10}=-\frac{2}{5}$，则$\frac{AD}{10}=\frac{2}{5}$，解得$AD = 10×\frac{2}{5}= 4$。
对$(\frac{AE}{15})^2 = \frac{4}{25}$求解：
等式两边同时开平方可得$\frac{AE}{15}=\pm\sqrt{\frac{4}{25}}=\pm\frac{2}{5}$。
因为$AE$为线段长度，大于$0$，所以舍去$\frac{AE}{15}=-\frac{2}{5}$，则$\frac{AE}{15}=\frac{2}{5}$，解得$AE = 15×\frac{2}{5}= 6$。
【答案】：
$AD = 4$，$AE = 6$。