《2025年中学生世界九年级数学上册沪教版五四制》

9. 如图,在梯形$ABCD$中,已知$AD// BC$,$EF$是梯形的中位线.若$\overrightarrow{AD}= \vec{a}$,$|\overrightarrow{AD}|= 2$,$|\overrightarrow{BC}|= 3$,则$\overrightarrow{EF}= $$\frac{5}{4}\vec{a}$.(结果用向量表示)

答案： 【解析】：本题考查梯形的中位线性质以及向量的运算。
梯形的中位线性质：梯形的中位线平行于两底，并且等于两底和的一半。
向量的数乘运算：实数与向量相乘，结果仍为向量。
根据梯形的中位线性质，有$EF=\frac{AD + BC}{2}$。
已知$\overrightarrow{AD}=\vec{a}$，$|\overrightarrow{AD}| = 2$，$|\overrightarrow{BC}| = 3$，且$AD// BC$，所以$\overrightarrow{BC}$与$\overrightarrow{AD}$方向相同，可设$\overrightarrow{BC}=k\vec{a}(k\gt0)$。
由$|\overrightarrow{BC}| = 3$，$|\overrightarrow{AD}| = 2$，可得$|k\vec{a}| = 3$，因为$|\vec{a}| = 2$，所以$k|\vec{a}| = 3$，即$2k = 3$，解得$k=\frac{3}{2}$，所以$\overrightarrow{BC}=\frac{3}{2}\vec{a}$。
根据梯形中位线性质求$\overrightarrow{EF}$：
因为$EF$是梯形$ABCD$的中位线，所以$\overrightarrow{EF}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{BC})$。
将$\overrightarrow{AD}=\vec{a}$，$\overrightarrow{BC}=\frac{3}{2}\vec{a}$代入上式可得：
$\overrightarrow{EF}=\frac{1}{2}(\vec{a}+\frac{3}{2}\vec{a})=\frac{1}{2}×\frac{5}{2}\vec{a}=\frac{5}{4}\vec{a}$。
【答案】：$\frac{5}{4}\vec{a}$。

10. 计算：
(1)$3(2\vec{a}+\vec{b})-(\vec{a}-\vec{b})$； (2)$-\frac{3}{2}\vec{a}-(\vec{a}-\frac{3}{2}\vec{b})$.

答案： 【解析】：
本题考查向量的数乘和向量的加减运算。向量的数乘满足分配律和结合律，向量的加减遵循三角形法则或平行四边形法则。
对于形如$k\vec{a} + l\vec{b}$的表达式，我们只需分别将系数与向量相乘，然后根据向量的加减法规则进行计算即可。
【答案】：
(1)
解：原式
$= 3(2\vec{a}+\vec{b})-(\vec{a}-\vec{b})$
$= 6\vec{a} + 3\vec{b} - \vec{a} + \vec{b}$
$= 5\vec{a} + 4\vec{b}$
(2)
解：原式
$= -\frac{3}{2}\vec{a}-(\vec{a}-\frac{3}{2}\vec{b})$
$= -\frac{3}{2}\vec{a} - \vec{a} + \frac{3}{2}\vec{b}$
$= -\frac{5}{2}\vec{a} + \frac{3}{2}\vec{b}$

11. 计算：
(1)$(\vec{a}+\vec{b}-3\vec{c})-2(\vec{a}-\frac{3}{2}\vec{b})$； (2)$2(\vec{a}-\frac{1}{2}\vec{b})-3(\frac{1}{3}\vec{a}+\vec{b})$.

答案： 【解析】：
本题考查向量的线性运算，包括向量的加法、减法和数乘。
对于第一个表达式，我们需要先对表达式进行展开，然后合并同类项。
对于第二个表达式，同样先对表达式进行展开，再合并同类项。
【答案】：
(1)
解：
$\begin{aligned}&(\vec{a}+\vec{b}-3\vec{c})-2(\vec{a}-\frac{3}{2}\vec{b}) \\&= \vec{a} + \vec{b} - 3\vec{c} - 2\vec{a} + 3\vec{b} \\&= -\vec{a} + 4\vec{b} - 3\vec{c}\end{aligned}$
(2)
解：
$\begin{aligned}&2(\vec{a}-\frac{1}{2}\vec{b})-3(\frac{1}{3}\vec{a}+\vec{b}) \\&= 2\vec{a} - \vec{b} - \vec{a} - 3\vec{b} \\&= \vec{a} - 4\vec{b}\end{aligned}$。

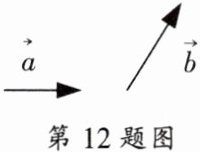
12. 如图,已知不平行的向量$\vec{a}与向量\vec{b}$,求作:向量$2\vec{a}+\vec{b}$.

答案： 解：1. 任取一点O，作向量$\overrightarrow{OA}=2\vec{a}$（即作$\overrightarrow{OA}$与$\vec{a}$同向，长度为$\vec{a}$的2倍）；
2. 以点A为起点，作向量$\overrightarrow{AB}=\vec{b}$（即作$\overrightarrow{AB}$与$\vec{b}$同向，长度相等）；
3. 连接OB，则向量$\overrightarrow{OB}=2\vec{a}+\vec{b}$。
（注：此处需根据实际作图步骤呈现，上述为文字描述作图过程，实际答题中应配合图形完成，由于文本限制，图形略）