《2025年中学生世界九年级数学上册沪教版五四制》

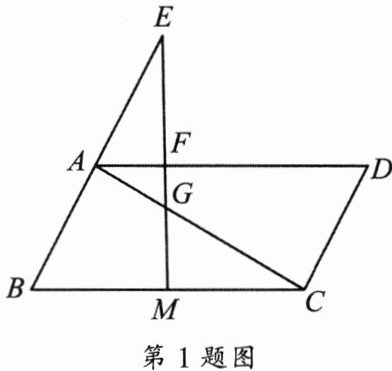
1. 已知: 如图, 在平行四边形 $ A B C D $ 中, $ M $ 是边 $ B C $ 的中点, $ E $ 是边 $ B A $ 延长线上的一点, 联结 $ E M $, 分别交线段 $ A D $ 于点 $ F 、 A C $ 于点 $ G $.
(1) 求证: $ \frac{G F}{G M}= \frac{E F}{E M} $;
(2) 当 $ B C^{2}= 2 B A \cdot B E $ 时, 求证: $ \angle E M B= \angle A C D $.

答案：
(1) 证明：
∵ 四边形 $ABCD$ 是平行四边形，
∴ $AD // BC$，$AD = BC$。
∵ $M$ 是 $BC$ 中点，
∴ $MC = \frac{1}{2}BC$。
∵ $AD // BC$，
∴ $\triangle AFG \sim \triangle CMG$，$\triangle AEF \sim \triangle BEM$。
∴ $\frac{GF}{GM} = \frac{AF}{MC}$，$\frac{EF}{EM} = \frac{AF}{BM}$。
∵ $BM = MC$，
∴ $\frac{GF}{GM} = \frac{EF}{EM}$。
(2) 证明：
∵ $BC^2 = 2BA \cdot BE$，$BC = 2BM$，
∴ $(2BM)^2 = 2BA \cdot BE$，即 $2BM^2 = BA \cdot BE$，
∴ $\frac{BA}{BM} = \frac{BM}{BE}$。
∵ $\angle B = \angle B$，
∴ $\triangle BAM \sim \triangle BME$，
∴ $\angle BMA = \angle BEM$。
∵ $AB // CD$，
∴ $\angle ACD = \angle BAC$。
∵ $AD // BC$，
∴ $\angle BAC = \angle BMA$，
∴ $\angle EMB = \angle ACD$。

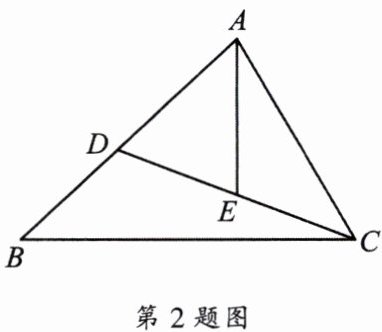
2. 已知: 如图, 在 $ \triangle A B C $ 中, 点 $ D $ 在边 $ A B $ 上, 点 $ E $ 在线段 $ C D $ 上, 且 $ \angle A C D= \angle B= \angle B A E $.
(1) 求证: $ \frac{A D}{B C}= \frac{D E}{A C} $;
(2) 当点 $ E $ 为 $ C D $ 中点时, 求证: $ \frac{A E^{2}}{C E^{2}}= \frac{A B}{A D} $.

(1) 证明：设∠ACD=∠B=∠BAE=α，
∵∠BAE=α，∠B=α，∴∠AEB=180°-∠BAE-∠B=180°-2α，
∵∠AEC=180°-∠AEB，∴∠AEC=2α，
∵∠ACD=α，∴∠DAC=180°-∠ADC-∠ACD=180°-∠ADC-α，
又∠ADC=∠B+∠BCD=α+∠BCD，∴∠DAC=180°-(α+∠BCD)-α=180°-2α-∠BCD，
∵∠ACB=∠ACD+∠BCD=α+∠BCD，∠BAC=∠BAE+∠EAC=α+∠EAC，
在△ABC中，∠BAC+∠B+∠ACB=180°，即(α+∠EAC)+α+(α+∠BCD)=180°，
∴∠EAC=180°-3α-∠BCD，
又∠DAC=∠BAC-∠BAE=(α+∠EAC)-α=∠EAC，∴∠EAC=180°-2α-∠BCD，
∴∠AEC=2α，∠EAC=180°-2α-∠BCD，∠ACD=α，
在△AEC中，∠EAC+∠AEC+∠ACD=180°-2α-∠BCD+2α+α=180°+α-∠BCD=180°，
∴α=∠BCD，即∠BCD=α，
∴∠ADC=α+∠BCD=2α，∴∠ADC=∠AEC，
∵∠ACD=∠B=α，∴△ADC∽△CEA，
∴AD/CE=AC/AE，即AD/AC=CE/AE，
∵∠BAE=∠B=α，∴AE=BE，
∠AED=180°-∠AEC=180°-2α，∠BEC=∠AEC-∠AEB=2α-(180°-2α)=4α-180°，
由∠BCD=α，∠B=α，∴△BCE中，∠BEC=180°-α-α=180°-2α，
∴∠AED=∠BEC，
∠ADE=180°-∠ADC=180°-2α，∴∠ADE=∠BCE，
∴△ADE∽△BCE，
∴AD/BC=DE/CE，
又△ADC∽△CEA得AD/AC=CE/AE，且AE=BE，△ADE∽△BCE得AD/BC=DE/CE，
综上，AD/BC=DE/AC。
(2) 证明：∵E为CD中点，∴CE=DE=CD/2，
由(1)△ADC∽△CEA，得AD/CE=AC/AE=CD/AC，
∴AD/CE=CD/AC，即AD·AC=CE·CD=CE·2CE=2CE²，
AC/AE=CD/AC，即AC²=AE·CD=AE·2CE，
△ABE中，AE=BE，∠BAE=∠B=α，
△ABC中，AC²=AB·AD（由∠ACD=∠B，∠BAC=∠BAC得△ABC∽△ACD），
∴AB·AD=AE·2CE，
由AD·AC=2CE²，得AC=2CE²/AD，
代入AC²=AE·2CE，(2CE²/AD)²=AE·2CE，
4CE⁴/AD²=2AE·CE，即2CE³/AD²=AE，
AB·AD=AE·2CE=2CE·(2CE³/AD²)=4CE⁴/AD²，
∴AB=4CE⁴/AD³，
AE²/CE²=(AE/CE)²，由AC²=AE·2CE得AE=AC²/(2CE)，
∴AE²/CE²=AC⁴/(4CE⁴)，
又AC²=AB·AD，∴AC⁴=AB²·AD²，
∴AE²/CE²=AB²·AD²/(4CE⁴)=AB²·AD²/(2AD·AC·2CE²)=AB²·AD/(2AC·2CE²)，
由AD·AC=2CE²，得AE²/CE²=AB²·AD/(AC·AD·AC)=AB²/AC²=AB²/(AB·AD)=AB/AD，
即AE²/CE²=AB/AD。

答案：
(1) 证明：设∠ACD=∠B=∠BAE=α，
∵∠BAE=α，∠B=α，
∴∠AEB=180°-∠BAE-∠B=180°-2α，
∵∠AEC=180°-∠AEB，
∴∠AEC=2α，
∵∠ACD=α，
∴∠DAC=180°-∠ADC-∠ACD=180°-∠ADC-α，
又∠ADC=∠B+∠BCD=α+∠BCD，
∴∠DAC=180°-(α+∠BCD)-α=180°-2α-∠BCD，
∵∠ACB=∠ACD+∠BCD=α+∠BCD，∠BAC=∠BAE+∠EAC=α+∠EAC，
在△ABC中，∠BAC+∠B+∠ACB=180°，即(α+∠EAC)+α+(α+∠BCD)=180°，
∴∠EAC=180°-3α-∠BCD，
又∠DAC=∠BAC-∠BAE=(α+∠EAC)-α=∠EAC，
∴∠EAC=180°-2α-∠BCD，
∴∠AEC=2α，∠EAC=180°-2α-∠BCD，∠ACD=α，
在△AEC中，∠EAC+∠AEC+∠ACD=180°-2α-∠BCD+2α+α=180°+α-∠BCD=180°，
∴α=∠BCD，即∠BCD=α，
∴∠ADC=α+∠BCD=2α，
∴∠ADC=∠AEC，
∵∠ACD=∠B=α，
∴△ADC∽△CEA，
∴AD/CE=AC/AE，即AD/AC=CE/AE，
∵∠BAE=∠B=α，
∴AE=BE，
∠AED=180°-∠AEC=180°-2α，∠BEC=∠AEC-∠AEB=2α-(180°-2α)=4α-180°，
由∠BCD=α，∠B=α，
∴△BCE中，∠BEC=180°-α-α=180°-2α，
∴∠AED=∠BEC，
∠ADE=180°-∠ADC=180°-2α，
∴∠ADE=∠BCE，
∴△ADE∽△BCE，
∴AD/BC=DE/CE，
又△ADC∽△CEA得AD/AC=CE/AE，且AE=BE，△ADE∽△BCE得AD/BC=DE/CE，
综上，AD/BC=DE/AC。
(2) 证明：
∵E为CD中点，
∴CE=DE=CD/2，
由
(1)△ADC∽△CEA，得AD/CE=AC/AE=CD/AC，
∴AD/CE=CD/AC，即AD·AC=CE·CD=CE·2CE=2CE²，
AC/AE=CD/AC，即AC²=AE·CD=AE·2CE，
△ABE中，AE=BE，∠BAE=∠B=α，
△ABC中，AC²=AB·AD（由∠ACD=∠B，∠BAC=∠BAC得△ABC∽△ACD），
∴AB·AD=AE·2CE，
由AD·AC=2CE²，得AC=2CE²/AD，
代入AC²=AE·2CE，(2CE²/AD)²=AE·2CE，
4CE⁴/AD²=2AE·CE，即2CE³/AD²=AE，
AB·AD=AE·2CE=2CE·(2CE³/AD²)=4CE⁴/AD²，
∴AB=4CE⁴/AD³，
AE²/CE²=(AE/CE)²，由AC²=AE·2CE得AE=AC²/(2CE)，
∴AE²/CE²=AC⁴/(4CE⁴)，
又AC²=AB·AD，
∴AC⁴=AB²·AD²，
∴AE²/CE²=AB²·AD²/(4CE⁴)=AB²·AD²/(2AD·AC·2CE²)=AB²·AD/(2AC·2CE²)，
由AD·AC=2CE²，得AE²/CE²=AB²·AD/(AC·AD·AC)=AB²/AC²=AB²/(AB·AD)=AB/AD，
即AE²/CE²=AB/AD。