《2025年中学生世界九年级数学上册沪教版五四制》

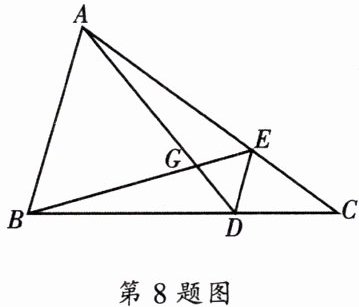
8. 如图,在$\triangle ABC$中,已知$BE$、$AD相交于点G$,$BD = 2CD$,$AE = 2EC$,$\overrightarrow {AB} = \overrightarrow {a}$,$\overrightarrow {AC} = \overrightarrow {b}$,用向量$\overrightarrow {a}与\overrightarrow {b}表示\overrightarrow {BE}和\overrightarrow {BG}$.

答案： 解：
$\overrightarrow{BE} = \overrightarrow{AE} - \overrightarrow{AB}$
$\because AE = 2EC$，$\overrightarrow{AC} = \overrightarrow{b}$
$\therefore \overrightarrow{AE} = \frac{2}{3}\overrightarrow{AC} = \frac{2}{3}\overrightarrow{b}$
$\because \overrightarrow{AB} = \overrightarrow{a}$
$\therefore \overrightarrow{BE} = \frac{2}{3}\overrightarrow{b} - \overrightarrow{a} = -\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}$
$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD}$
$\because BD = 2CD$，$\overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB} = \overrightarrow{b} - \overrightarrow{a}$
$\therefore \overrightarrow{BD} = \frac{2}{3}\overrightarrow{BC} = \frac{2}{3}(\overrightarrow{b} - \overrightarrow{a})$
$\therefore \overrightarrow{AD} = \overrightarrow{a} + \frac{2}{3}(\overrightarrow{b} - \overrightarrow{a}) = \frac{1}{3}\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}$
设$\overrightarrow{AG} = t\overrightarrow{AD} = \frac{t}{3}\overrightarrow{a} + \frac{2t}{3}\overrightarrow{b}$，则$\overrightarrow{BG} = \overrightarrow{AG} - \overrightarrow{AB} = \frac{t}{3}\overrightarrow{a} + \frac{2t}{3}\overrightarrow{b} - \overrightarrow{a} = ( \frac{t}{3} - 1 )\overrightarrow{a} + \frac{2t}{3}\overrightarrow{b}$
又设$\overrightarrow{BG} = s\overrightarrow{BE} = s(-\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}) = -s\overrightarrow{a} + \frac{2s}{3}\overrightarrow{b}$
$\therefore \begin{cases} \frac{t}{3} - 1 = -s \\ \frac{2t}{3} = \frac{2s}{3} \end{cases}$
解得$t = s = \frac{3}{4}$
$\therefore \overrightarrow{BG} = -\frac{3}{4}\overrightarrow{a} + \frac{2}{3} × \frac{3}{4}\overrightarrow{b} = -\frac{3}{4}\overrightarrow{a} + \frac{1}{2}\overrightarrow{b}$
综上，$\overrightarrow{BE} = -\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}$，$\overrightarrow{BG} = -\frac{3}{4}\overrightarrow{a} + \frac{1}{2}\overrightarrow{b}$

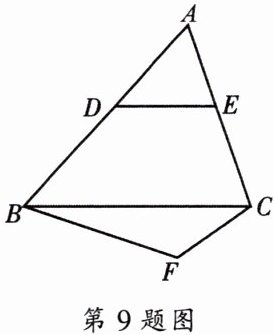
9. 如图,已知$F为\triangle ABC$外一点,点$D$、$E分别在边AB$、$AC$上,且$\frac {AD}{DB} = \frac {2}{3}$,$DE// BC$.若$\overrightarrow {DE} = \overrightarrow {a}$,$\overrightarrow {FC} = \overrightarrow {b}$,试用$\overrightarrow {a}和\overrightarrow {b}表示\overrightarrow {BF}$.

答案： 解：
∵ $ DE // BC $，$\frac{AD}{DB} = \frac{2}{3}$，
∴ $\frac{AD}{AB} = \frac{2}{5}$，$\triangle ADE \sim \triangle ABC$，相似比为$\frac{2}{5}$。
∴ $\overrightarrow{BC} = \frac{5}{2}\overrightarrow{DE} = \frac{5}{2}\overrightarrow{a}$。
∵ $\overrightarrow{BF} = \overrightarrow{BC} + \overrightarrow{CF}$，且$\overrightarrow{CF} = -\overrightarrow{FC} = -\overrightarrow{b}$，
∴ $\overrightarrow{BF} = \frac{5}{2}\overrightarrow{a} - \overrightarrow{b}$。
答案：$\overrightarrow{BF} = \frac{5}{2}\overrightarrow{a} - \overrightarrow{b}$