《2025年中学生世界九年级数学上册沪教版五四制》

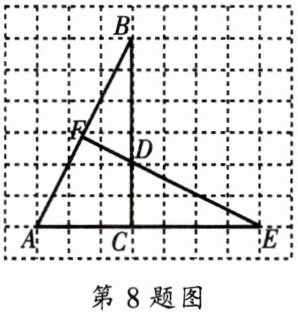
8. 如图, 网格中的每个小正方形的边长都是1, 我们把每个小正方形的顶点叫做 “格点”.$△ACB和△DCE$的顶点都在“格点”上,线段ED的延长线交AB于点F.
(1)求证:$△ACB\backsim △DCE;$
(2)求证:$EF⊥AB.$

答案：
(1)证明：由网格可知，$AC=3$，$BC=6$，$CD=2$，$CE=4$，$\angle ACB=\angle DCE=90^\circ$。
$\because \frac{AC}{DC}=\frac{3}{2}$，$\frac{BC}{EC}=\frac{6}{4}=\frac{3}{2}$，
$\therefore \frac{AC}{DC}=\frac{BC}{EC}$。
又$\because \angle ACB=\angle DCE$，
$\therefore \triangle ACB\backsim\triangle DCE$。
(2)证明：$\because \triangle ACB\backsim\triangle DCE$，
$\therefore \angle ABC=\angle DEC$。
$\because \angle ABC+\angle BAC=90^\circ$，
$\therefore \angle DEC+\angle BAC=90^\circ$。
$\because \angle DEC=\angle AEF$，
$\therefore \angle AEF+\angle BAC=90^\circ$，
$\therefore \angle AFE=90^\circ$，即$EF\perp AB$。

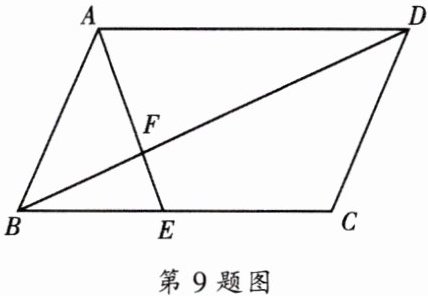
9. 如图,在平行四边形ABCD中,已知AE交BC于点E,交BD于点F,且$BE^{2}= EF\cdot EA.$
求证:$AB^{2}= BF\cdot BD.$

答案： 证明：
∵ $ BE^2 = EF \cdot EA $，
∴ $ \frac{BE}{EF} = \frac{EA}{BE} $。
∵ $ \angle BEF = \angle AEB $，
∴ $ \triangle BEF \sim \triangle AEB $（两边对应成比例且夹角相等的两个三角形相似）。
∴ $ \angle EBF = \angle EAB $。
∵ 四边形 $ ABCD $ 是平行四边形，
∴ $ AD // BC $，
∴ $ \angle ADB = \angle EBF $（两直线平行，内错角相等）。
∴ $ \angle ADB = \angle EAB $。
∵ $ \angle ABF = \angle DBA $，
∴ $ \triangle ABF \sim \triangle DBA $（两角分别相等的两个三角形相似）。
∴ $ \frac{AB}{DB} = \frac{BF}{AB} $，
∴ $ AB^2 = BF \cdot BD $。

10. 如图,在$△ABC$中,已知$AB= AC$,点D、E分别在边BC、AC上,且满足$BD= 2CD,AE= CE$,联结DE并延长,交BA的延长线于点F,联结AD.
(1)求证:$△CDE\backsim △BDA;$
(2)求证:$AB= AF.$

答案：
(1)证明：
∵AB=AC，
∴∠B=∠C。
∵BD=2CD，设CD=x，则BD=2x，BC=3x。
∵AE=CE，
∴CE=1/2AC，又AB=AC，
∴CE=1/2AB。
∴CE/AB=1/2，CD/BD=x/(2x)=1/2，
∴CE/AB=CD/BD。
在△CDE和△BDA中，∠C=∠B，CE/AB=CD/BD，
∴△CDE∽△BDA。
(2)证明：由
(1)知△CDE∽△BDA，
∴DE/DA=CE/AB=1/2，∠CDE=∠BDA。
∵∠CDE=∠BDF，
∴∠BDA=∠BDF，即AD平分∠BDF。
过点A作AG//BC交DF于点G，
∴△AGF∽△BDF，△AGE∽△CDE。
∴AG/BD=AF/BF，AG/CD=AE/CE。
∵AE=CE，
∴AG/CD=1，即AG=CD=x。
∵BD=2x，
∴AG/BD=x/(2x)=1/2，
∴AF/BF=1/2，即BF=2AF。
∵BF=AB+AF，
∴AB+AF=2AF，
∴AB=AF。

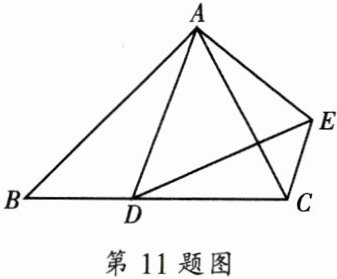
11. 如图,在$△ABC$中,已知$∠ADE= ∠B,∠BAC= ∠DAE.$
(1)求证:$\frac {AD}{AB}= \frac {AE}{AC};$
(2)当$∠BAC= 90^{\circ }$时,求证:$EC⊥BC.$

答案：
(1)证明：因为∠BAC=∠DAE，所以∠BAC - ∠DAC = ∠DAE - ∠DAC，即∠BAD=∠CAE。又因为∠ADE=∠B，所以△ADE∽△ABC，所以AD/AB=AE/AC。
(2)证明：由
(1)知AD/AB=AE/AC，又∠BAD=∠CAE，所以△ABD∽△ACE，所以∠ACE=∠B。因为∠BAC=90°，所以∠B+∠ACB=90°，所以∠ACE+∠ACB=90°，即∠BCE=90°，所以EC⊥BC。