1. 如图,已知$a// b// c,AE= CE= 5,BF= 6$,则BD的长为 (
A.10;
B.6;
C.12;
D.16.
C
)A.10;
B.6;
C.12;
D.16.
答案:
【解析】:本题可根据平行线分线段成比例定理来求解$BD$的长度。
已知$a// b// c$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
可得$\frac{AE}{EC}=\frac{BF}{FD}$。
因为$AE = CE = 5$,$BF = 6$,将其代入到$\frac{AE}{EC}=\frac{BF}{FD}$中,可得$\frac{5}{5}=\frac{6}{FD}$,即$FD = 6$。
那么$BD=BF + FD$,把$BF = 6$,$FD = 6$代入可得$BD=6 + 6 = 12$。
【答案】:C。
已知$a// b// c$,根据平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
可得$\frac{AE}{EC}=\frac{BF}{FD}$。
因为$AE = CE = 5$,$BF = 6$,将其代入到$\frac{AE}{EC}=\frac{BF}{FD}$中,可得$\frac{5}{5}=\frac{6}{FD}$,即$FD = 6$。
那么$BD=BF + FD$,把$BF = 6$,$FD = 6$代入可得$BD=6 + 6 = 12$。
【答案】:C。
2. 如图,已知$l_{1}// l_{2}// l_{3}$,则下列结论正确的是 (

A.$\frac {AB}{BC}= \frac {DE}{EF}$;
B.$\frac {AD}{BE}= \frac {BE}{CF}$;
C.$\frac {AB}{AC}= \frac {BE}{CF}$;
D.$\frac {AB}{AC}= \frac {DE}{EF}$.
A
)
A.$\frac {AB}{BC}= \frac {DE}{EF}$;
B.$\frac {AD}{BE}= \frac {BE}{CF}$;
C.$\frac {AB}{AC}= \frac {BE}{CF}$;
D.$\frac {AB}{AC}= \frac {DE}{EF}$.
答案:
证明:
∵$l_{1}// l_{2}// l_{3}$,
∴由平行线分线段成比例定理得:$\frac{AB}{BC}=\frac{DE}{EF}$。
A
∵$l_{1}// l_{2}// l_{3}$,
∴由平行线分线段成比例定理得:$\frac{AB}{BC}=\frac{DE}{EF}$。
A
3. 如图,已知$AB// CD// EF,BD:DF= 2:5$,那么下列结论正确的是 (
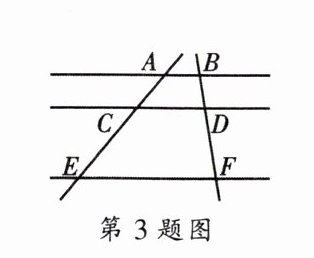
A.$AC:AE= 2:5$;
B.$AB:CD= 2:5$;
C.$CD:EF= 2:5$;
D.$CE:EA= 5:7$.
D
)
A.$AC:AE= 2:5$;
B.$AB:CD= 2:5$;
C.$CD:EF= 2:5$;
D.$CE:EA= 5:7$.
答案:
【解析】:本题可根据平行线分线段成比例定理来逐一分析选项。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知$AB// CD// EF$,根据平行线分线段成比例定理可得:
$\frac{AC}{CE}=\frac{BD}{DF}$,因为$BD:DF = 2:5$,所以$\frac{AC}{CE}=\frac{2}{5}$。
选项A:判断$AC:AE = 2:5$是否正确
由$\frac{AC}{CE}=\frac{2}{5}$,可得$CE=\frac{5}{2}AC$,那么$AE=AC + CE=AC+\frac{5}{2}AC=\frac{7}{2}AC$,所以$\frac{AC}{AE}=\frac{AC}{\frac{7}{2}AC}=\frac{2}{7}$,即$AC:AE = 2:7\neq2:5$,故选项A错误。
选项B:判断$AB:CD = 2:5$是否正确
仅根据$AB// CD// EF$和$BD:DF = 2:5$,无法得出$AB$与$CD$的比值为$2:5$,故选项B错误。
选项C:判断$CD:EF = 2:5$是否正确
同理,仅由已知条件不能得出$CD$与$EF$的比值为$2:5$,故选项C错误。
选项D:判断$CE:EA = 5:7$是否正确
因为$\frac{AC}{CE}=\frac{2}{5}$,设$AC = 2x$,则$CE = 5x$,那么$AE=AC + CE=2x + 5x = 7x$,所以$\frac{CE}{AE}=\frac{5x}{7x}=\frac{5}{7}$,即$CE:EA = 5:7$,故选项D正确。
【答案】:D
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知$AB// CD// EF$,根据平行线分线段成比例定理可得:
$\frac{AC}{CE}=\frac{BD}{DF}$,因为$BD:DF = 2:5$,所以$\frac{AC}{CE}=\frac{2}{5}$。
选项A:判断$AC:AE = 2:5$是否正确
由$\frac{AC}{CE}=\frac{2}{5}$,可得$CE=\frac{5}{2}AC$,那么$AE=AC + CE=AC+\frac{5}{2}AC=\frac{7}{2}AC$,所以$\frac{AC}{AE}=\frac{AC}{\frac{7}{2}AC}=\frac{2}{7}$,即$AC:AE = 2:7\neq2:5$,故选项A错误。
选项B:判断$AB:CD = 2:5$是否正确
仅根据$AB// CD// EF$和$BD:DF = 2:5$,无法得出$AB$与$CD$的比值为$2:5$,故选项B错误。
选项C:判断$CD:EF = 2:5$是否正确
同理,仅由已知条件不能得出$CD$与$EF$的比值为$2:5$,故选项C错误。
选项D:判断$CE:EA = 5:7$是否正确
因为$\frac{AC}{CE}=\frac{2}{5}$,设$AC = 2x$,则$CE = 5x$,那么$AE=AC + CE=2x + 5x = 7x$,所以$\frac{CE}{AE}=\frac{5x}{7x}=\frac{5}{7}$,即$CE:EA = 5:7$,故选项D正确。
【答案】:D
4. 如图,已知直线$l_{1}// l_{2}// l_{3}$,另两条直线分别交$l_{1}$、$l_{2}$、$l_{3}$于点A、B、C及点D、E、F,且$AB= 3,DE= 4,EF= 2$,则 (
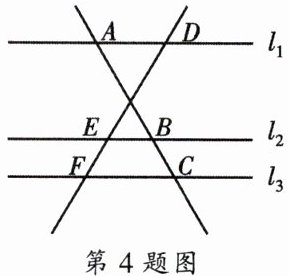
A.$BC:DE= 1:2$;
B.$BC:DE= 2:3$;
C.$BC\cdot DE= 8$;
D.$BC\cdot DE= 6$.
D
)
A.$BC:DE= 1:2$;
B.$BC:DE= 2:3$;
C.$BC\cdot DE= 8$;
D.$BC\cdot DE= 6$.
答案:
【解析】:本题可根据平行线分线段成比例定理来求解$BC$与$DE$的关系。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知直线$l_{1}// l_{2}// l_{3}$,直线$AD$、$BC$分别交$l_{1}$、$l_{2}$、$l_{3}$于点$A$、$B$、$C$及点$D$、$E$、$F$,则可得$\frac{AB}{BC}=\frac{DE}{EF}$。
已知$AB = 3$,$DE = 4$,$EF = 2$,将其代入$\frac{AB}{BC}=\frac{DE}{EF}$中,可得$\frac{3}{BC}=\frac{4}{2}$。
交叉相乘可得:$4× BC=3×2$,即$4BC = 6$,解得$BC=\frac{6}{4}=\frac{3}{2}$。
接下来分析$BC$与$DE$的关系:
选项A:计算$BC:DE=\frac{3}{2}:4=\frac{3}{2}×\frac{1}{4}=\frac{3}{8}=3:8\neq1:2$,所以选项A错误。
选项B:计算$BC:DE=\frac{3}{2}:4 = 3:8\neq2:3$,所以选项B错误。
选项C:计算$BC\cdot DE=\frac{3}{2}×4 = 6\neq8$,所以选项C错误。
选项D:计算$BC\cdot DE=\frac{3}{2}×4 = 6$,所以选项D正确。
【答案】:D
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知直线$l_{1}// l_{2}// l_{3}$,直线$AD$、$BC$分别交$l_{1}$、$l_{2}$、$l_{3}$于点$A$、$B$、$C$及点$D$、$E$、$F$,则可得$\frac{AB}{BC}=\frac{DE}{EF}$。
已知$AB = 3$,$DE = 4$,$EF = 2$,将其代入$\frac{AB}{BC}=\frac{DE}{EF}$中,可得$\frac{3}{BC}=\frac{4}{2}$。
交叉相乘可得:$4× BC=3×2$,即$4BC = 6$,解得$BC=\frac{6}{4}=\frac{3}{2}$。
接下来分析$BC$与$DE$的关系:
选项A:计算$BC:DE=\frac{3}{2}:4=\frac{3}{2}×\frac{1}{4}=\frac{3}{8}=3:8\neq1:2$,所以选项A错误。
选项B:计算$BC:DE=\frac{3}{2}:4 = 3:8\neq2:3$,所以选项B错误。
选项C:计算$BC\cdot DE=\frac{3}{2}×4 = 6\neq8$,所以选项C错误。
选项D:计算$BC\cdot DE=\frac{3}{2}×4 = 6$,所以选项D正确。
【答案】:D
5. 已知线段a、b、c,且$x= \frac {bc}{a}$,求作x,则下列作图正确的是 (
C
)
答案:
【解析】:本题主要考查了平行线分线段成比例定理的应用。
根据平行线分线段成比例定理,如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
在本题中,已知$x=\frac{bc}{a}$,需要找到一个图形,使得通过平行线分线段成比例定理能够推导出这个等式。
观察选项,发现只有选项C的图形满足条件。
在选项C中,如果过上顶点作一边的平行线,根据平行线分线段成比例定理,可以得到$\frac{x}{a}=\frac{b}{c}$的等价形式,即$x=\frac{bc}{a}$,与题目给出的等式一致。
【答案】:C
根据平行线分线段成比例定理,如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
在本题中,已知$x=\frac{bc}{a}$,需要找到一个图形,使得通过平行线分线段成比例定理能够推导出这个等式。
观察选项,发现只有选项C的图形满足条件。
在选项C中,如果过上顶点作一边的平行线,根据平行线分线段成比例定理,可以得到$\frac{x}{a}=\frac{b}{c}$的等价形式,即$x=\frac{bc}{a}$,与题目给出的等式一致。
【答案】:C
6. 如图,已知$l_{1}// l_{2}// l_{3},AB= 3,AC= 5,DF= 10$,则EF的长是______.


4
答案:
【解析】:本题可根据平行线分线段成比例定理来求解$EF$的长度。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知$l_{1}// l_{2}// l_{3}$,则有$\frac{AB}{AC}=\frac{DE}{DF}$。
先根据已知条件求出$DE$的长度,再通过$DF$的长度求出$EF$的长度。
【答案】:解:
∵$l_{1}// l_{2}// l_{3}$,
∴$\frac{AB}{AC}=\frac{DE}{DF}$。
已知$AB = 3$,$AC = 5$,$DF = 10$,代入上式可得:
$\frac{3}{5}=\frac{DE}{10}$
交叉相乘可得:$5DE = 3×10$,即$5DE = 30$,
两边同时除以$5$,解得$DE = 6$。
因为$DF = 10$,$EF=DF - DE$,所以$EF = 10 - 6 = 4$。
故答案为$4$。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
已知$l_{1}// l_{2}// l_{3}$,则有$\frac{AB}{AC}=\frac{DE}{DF}$。
先根据已知条件求出$DE$的长度,再通过$DF$的长度求出$EF$的长度。
【答案】:解:
∵$l_{1}// l_{2}// l_{3}$,
∴$\frac{AB}{AC}=\frac{DE}{DF}$。
已知$AB = 3$,$AC = 5$,$DF = 10$,代入上式可得:
$\frac{3}{5}=\frac{DE}{10}$
交叉相乘可得:$5DE = 3×10$,即$5DE = 30$,
两边同时除以$5$,解得$DE = 6$。
因为$DF = 10$,$EF=DF - DE$,所以$EF = 10 - 6 = 4$。
故答案为$4$。
7. 如图,直线$l_{1}// l_{2}// l_{3}$,已知$AG= 0.6cm,BG= 1.2cm,CD= 1.5cm$,则$CH= $
0.5cm
.
答案:
【解析】:本题考查平行线分线段成比例定理。
由于$l_1// l_2// l_3$,
根据平行线分线段成比例定理,
有$\frac{AG}{GB}=\frac{CH}{HD}$。
已知$AG=0.6\text{cm}$,$BG=1.2\text{cm}$,$CD=1.5\text{cm}$,
设$CH=x\text{cm}$,则$HD=(1.5-x)\text{cm}$。
代入比例式,得$\frac{0.6}{1.2}=\frac{x}{1.5-x}$,
交叉相乘,得$0.6(1.5-x)=1.2x$,
展开并整理,得$0.9-0.6x=1.2x$,
移项并合并同类项,得$1.8x=0.9$,
解得$x=0.5$。
所以$CH=0.5\text{cm}$。
【答案】:$CH=0.5\text{cm}$。
由于$l_1// l_2// l_3$,
根据平行线分线段成比例定理,
有$\frac{AG}{GB}=\frac{CH}{HD}$。
已知$AG=0.6\text{cm}$,$BG=1.2\text{cm}$,$CD=1.5\text{cm}$,
设$CH=x\text{cm}$,则$HD=(1.5-x)\text{cm}$。
代入比例式,得$\frac{0.6}{1.2}=\frac{x}{1.5-x}$,
交叉相乘,得$0.6(1.5-x)=1.2x$,
展开并整理,得$0.9-0.6x=1.2x$,
移项并合并同类项,得$1.8x=0.9$,
解得$x=0.5$。
所以$CH=0.5\text{cm}$。
【答案】:$CH=0.5\text{cm}$。
8. 如图,已知梯形ABCD中,$AD// EF// BC,AE= BE,DC= 10$,则$DF= $
5
.
答案:
【解析】:本题可根据梯形中平行线所截得的线段对应成比例这一性质来求解$DF$的长度。
已知$AD// EF// BC$,$AE = BE$,根据梯形中平行线分线段成比例定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等;或者由平行线分线段成比例定理的推论,三条平行线截两条直线,所得的对应线段成比例。
在本题中,因为$AD// EF// BC$,所以$\frac{AE}{AB}=\frac{DF}{DC}$,又因为$AE = BE$,所以$AE:AB = 1:2$,即$\frac{DF}{DC}=\frac{1}{2}$。
已知$DC = 10$,将其代入$\frac{DF}{DC}=\frac{1}{2}$,即可求出$DF$的值。
【答案】:解:
∵$AD// EF// BC$,$AE = BE$,
∴$\frac{AE}{AB}=\frac{DF}{DC}$,且$\frac{AE}{AB}=\frac{1}{2}$,
∴$\frac{DF}{DC}=\frac{1}{2}$,
又
∵$DC = 10$,
∴$DF=\frac{1}{2}×10 = 5$。
故答案为$5$。
已知$AD// EF// BC$,$AE = BE$,根据梯形中平行线分线段成比例定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等;或者由平行线分线段成比例定理的推论,三条平行线截两条直线,所得的对应线段成比例。
在本题中,因为$AD// EF// BC$,所以$\frac{AE}{AB}=\frac{DF}{DC}$,又因为$AE = BE$,所以$AE:AB = 1:2$,即$\frac{DF}{DC}=\frac{1}{2}$。
已知$DC = 10$,将其代入$\frac{DF}{DC}=\frac{1}{2}$,即可求出$DF$的值。
【答案】:解:
∵$AD// EF// BC$,$AE = BE$,
∴$\frac{AE}{AB}=\frac{DF}{DC}$,且$\frac{AE}{AB}=\frac{1}{2}$,
∴$\frac{DF}{DC}=\frac{1}{2}$,
又
∵$DC = 10$,
∴$DF=\frac{1}{2}×10 = 5$。
故答案为$5$。
查看更多完整答案,请扫码查看


