《2025年中学生世界九年级数学上册沪教版五四制》

10. 在$△ABC$中,已知$∠C$为直角,$∠A$、$∠B$、$∠C$所对的边长分别为a、b、c,且$b= \sqrt {2},a= \sqrt {6}$,解这个三角形.

答案： 【解析】：
本题主要考查直角三角形的性质以及三角函数的应用。
在直角三角形中，已知两边长，可以利用勾股定理求出第三边长。
再利用三角函数求出其他角度。
【答案】：
解：
由于$∠C$为直角，可以利用勾股定理求出边长c，
$c = \sqrt{a^{2} + b^{2}} = \sqrt{6 + 2} = 2\sqrt{2}$，
利用三角函数求出$∠A$和$∠B$，
$\sin A = \frac{a}{c} = \frac{\sqrt{6}}{2\sqrt{2}} = \frac{\sqrt{3}}{2}$，
由此可得$∠A = 60°$，
在直角三角形中，两个锐角之和为$90°$，所以
$∠B = 90° - ∠A = 30°$，
所以，$△ABC$的三边长为$a = \sqrt{6}$，$b = \sqrt{2}$，$c = 2\sqrt{2}$，且$∠A = 60°$，$∠B = 30°$，$∠C = 90°$。

11. 由下列条件解题:在$Rt△ABC$中,$∠C= 90^{\circ }.$
(1)已知$a= 4,b= 8$,求c;
(2)已知$b= 10,∠B= 60^{\circ }$,求a、c;
(3)已知$sinA= \frac {2}{3},c= 6$,求a、b.

答案：
(1)解：在$Rt△ABC$中，$∠C=90^{\circ}$，$a=4$，$b=8$，由勾股定理得$c=\sqrt{a^{2}+b^{2}}=\sqrt{4^{2}+8^{2}}=\sqrt{16 + 64}=\sqrt{80}=4\sqrt{5}$。
(2)解：在$Rt△ABC$中，$∠C=90^{\circ}$，$∠B=60^{\circ}$，$b=10$。
因为$tanB=\frac{b}{a}$，所以$a=\frac{b}{tanB}=\frac{10}{tan60^{\circ}}=\frac{10}{\sqrt{3}}=\frac{10\sqrt{3}}{3}$。
因为$cosB=\frac{b}{c}$，所以$c=\frac{b}{cosB}=\frac{10}{cos60^{\circ}}=\frac{10}{\frac{1}{2}}=20$。
(3)解：在$Rt△ABC$中，$∠C=90^{\circ}$，$sinA=\frac{2}{3}$，$c=6$。
因为$sinA=\frac{a}{c}$，所以$a=c\cdot sinA=6×\frac{2}{3}=4$。
由勾股定理得$b=\sqrt{c^{2}-a^{2}}=\sqrt{6^{2}-4^{2}}=\sqrt{36 - 16}=\sqrt{20}=2\sqrt{5}$。

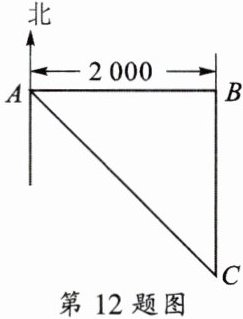
12. 如图,东、西两炮台A、B相距2000m,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东$45^{\circ }$的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.($\sqrt {2}\approx $1.414,精确到1m)

答案： 解：由题意得，∠BAC=90°-45°=45°，∠ABC=90°，AB=2000m。
在Rt△ABC中，∠BAC=45°，
∴∠ACB=180°-90°-45°=45°，
∴∠BAC=∠ACB，
∴BC=AB=2000m。
∵cos∠BAC=AB/AC，
∴AC=AB/cos45°=2000/(√2/2)=2000√2≈2000×1.414=2828m。
答：敌舰与炮台A的距离约为2828m，与炮台B的距离为2000m。

13. 在$△ABC$中,已知$∠C$为直角,$AC= 6,∠A的平分线AD= 4\sqrt {3}$,解这个直角三角形.

答案： 【解析】：
本题主要考察解直角三角形的相关知识，包括角平分线的性质、三角函数的应用以及勾股定理的使用。
首先，根据角平分线的性质，我们可以得到$\angle CAD = \angle BAD$。
接着，我们可以利用三角函数来求解$\angle CAD$，进而得到$\angle CAB$。
然后，我们可以利用三角函数求解$BC$和$AB$。
最后，我们利用勾股定理进行验证。
【答案】：
解：
在$Rt \bigtriangleup ACD$中，
$\cos\angle CAD = \frac{AC}{AD} = \frac{6}{4\sqrt{3}} = \frac{\sqrt{3}}{2}$，
∴ $\angle CAD = 30^{\circ}$，
∵ $AD$是$\angle BAC$的角平分线，
∴ $\angle CAB = 2\angle CAD = 60^{\circ}$，
∴ $\angle ABC = 180^{\circ} - 90^{\circ} - 60^{\circ} = 30^{\circ}$。
在$Rt \bigtriangleup ABC$中，
∵ $\frac{AC}{AB} = \cos\angle BAC = \cos 60^{\circ} = \frac{1}{2}$，
∴ $AB = 2AC = 2 × 6 = 12$，
∵ $\frac{BC}{AB} = \sin\angle BAC = \sin 60^{\circ} = \frac{\sqrt{3}}{2}$，
∴ $BC = \frac{\sqrt{3}}{2}AB = 6\sqrt{3}$。
验证：$AC^{2} + BC^{2} = 6^{2} + (6\sqrt{3})^{2} = 36 + 108 = 144 = 12^{2} = AB^{2}$，满足勾股定理。
故$Rt \bigtriangleup ABC$的三边长为$AC = 6$，$BC = 6\sqrt{3}$，$AB = 12$，$\angle CAB = 60^{\circ}$，$\angle ABC = 30^{\circ}$，$\angle C = 90^{\circ}$。

思维与拓展14
如图,已知在$Rt△ABC$中,$∠ACB= 90^{\circ }$,AD平分$∠BAC,DE⊥AB$,垂足为$E,AE= 16,sinB= \frac {4}{5}.$
(1)求BC的长;
(2)求$∠ADE$的正切值.

答案：
(1)解：
∵AD平分∠BAC，∠ACB=90°，DE⊥AB，
∴DC=DE，AC=AE=16。
在Rt△ABC中，∠ACB=90°，sinB=AC/AB=4/5，
∴16/AB=4/5，解得AB=20。
∴BE=AB - AE=20 - 16=4。
设DC=DE=x，BC=a，BD=a - x。
在Rt△BDE中，sinB=DE/BD=x/(a - x)=4/5，即5x=4(a - x)，5x=4a - 4x，9x=4a，x=4a/9。
在Rt△ABC中，BC²=AB² - AC²=20² - 16²=400 - 256=144，
∴BC=12。
(2)解：由
(1)知BC=12，x=4a/9=4×12/9=16/3，即DE=16/3。
在Rt△ADE中，tan∠ADE=AE/DE=16/(16/3)=3。