1. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,$sinA= \frac{5}{13}$,则$sinB$等于(
A.$\frac{12}{13}$;
B.$\frac{13}{12}$;
C.$\frac{5}{12}$;
D.$\frac{5}{13}$.
A
)A.$\frac{12}{13}$;
B.$\frac{13}{12}$;
C.$\frac{5}{12}$;
D.$\frac{5}{13}$.
答案:
解:在$Rt△ABC$中,$∠C=90^{\circ}$,则$∠A+∠B=90^{\circ}$,所以$∠B=90^{\circ}-∠A$。
因为$sinA=\frac{5}{13}$,设$BC=5k$,$AB=13k$($k>0$)。
由勾股定理得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{(13k)^{2}-(5k)^{2}}=12k$。
所以$sinB=\frac{AC}{AB}=\frac{12k}{13k}=\frac{12}{13}$。
答案:A。
因为$sinA=\frac{5}{13}$,设$BC=5k$,$AB=13k$($k>0$)。
由勾股定理得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{(13k)^{2}-(5k)^{2}}=12k$。
所以$sinB=\frac{AC}{AB}=\frac{12k}{13k}=\frac{12}{13}$。
答案:A。
2. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,$a = 1$,$c = 4$,则$sinA$的值是(
A.$\frac{\sqrt{15}}{15}$;
B.$\frac{1}{4}$;
C.$\frac{1}{3}$;
D.$\frac{\sqrt{15}}{4}$.
B
)A.$\frac{\sqrt{15}}{15}$;
B.$\frac{1}{4}$;
C.$\frac{1}{3}$;
D.$\frac{\sqrt{15}}{4}$.
答案:
解:在$Rt△ABC$中,$∠C=90^{\circ}$,
$sinA=\frac{a}{c}=\frac{1}{4}$.
答案:B
$sinA=\frac{a}{c}=\frac{1}{4}$.
答案:B
3. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,$AB = 10$,$sinB= \frac{2}{5}$,则$BC$的长是(
A.$2\sqrt{21}$;
B.4;
C.$\sqrt{21}$;
D.$\frac{\sqrt{21}}{50}$.
A
)A.$2\sqrt{21}$;
B.4;
C.$\sqrt{21}$;
D.$\frac{\sqrt{21}}{50}$.
答案:
【解析】:
本题主要考察直角三角形中三角函数的应用。
在直角三角形$ABC$中,已知$\angle C = 90^{\circ}$,$AB = 10$,以及$\sin B = \frac{2}{5}$。
根据正弦函数的定义,在直角三角形中,$\sin B = \frac{对边}{斜边} = \frac{AC}{AB}$。
代入已知条件,得$\frac{AC}{10} = \frac{2}{5}$,
解得$AC = 4$。
接下来,利用勾股定理求$BC$。
勾股定理公式为$AB^2 = AC^2 + BC^2$,
代入已知的$AB$和$AC$的值,得到$10^2 = 4^2 + BC^2$,
即$100 = 16 + BC^2$,
解得$BC^2 = 84$,
所以$BC = \sqrt{84} = 2\sqrt{21}$。
【答案】:
A.$2\sqrt{21}$。
本题主要考察直角三角形中三角函数的应用。
在直角三角形$ABC$中,已知$\angle C = 90^{\circ}$,$AB = 10$,以及$\sin B = \frac{2}{5}$。
根据正弦函数的定义,在直角三角形中,$\sin B = \frac{对边}{斜边} = \frac{AC}{AB}$。
代入已知条件,得$\frac{AC}{10} = \frac{2}{5}$,
解得$AC = 4$。
接下来,利用勾股定理求$BC$。
勾股定理公式为$AB^2 = AC^2 + BC^2$,
代入已知的$AB$和$AC$的值,得到$10^2 = 4^2 + BC^2$,
即$100 = 16 + BC^2$,
解得$BC^2 = 84$,
所以$BC = \sqrt{84} = 2\sqrt{21}$。
【答案】:
A.$2\sqrt{21}$。
4. 在$Rt△ABC$中,若各边长度都扩大2倍,则锐角$A$的正弦值和余弦值(
A.都没有变化;
B.都扩大2倍;
C.都缩小为$\frac{1}{2}$;
D.不能确定.
A
)A.都没有变化;
B.都扩大2倍;
C.都缩小为$\frac{1}{2}$;
D.不能确定.
答案:
【解析】:
本题主要考察锐角三角比的意义,特别是在直角三角形中,当各边长度发生变化时,锐角的正弦值和余弦值会如何变化。
在直角三角形中,锐角的正弦值定义为对边长度与斜边长度的比值,余弦值定义为邻边长度与斜边长度的比值。
设原始直角三角形$ABC$中,角$A$为锐角,对边$BC=a$,邻边$AC=b$,斜边$AB=c$。
根据正弦和余弦的定义,有:
$\sin A = \frac{a}{c}$,
$\cos A = \frac{b}{c}$,
当各边长度都扩大2倍时,新的对边长度为$2a$,新的邻边长度为$2b$,新的斜边长度为$2c$。
此时,新的正弦值和余弦值为:
$\sin A' = \frac{2a}{2c} = \frac{a}{c}$,
$\cos A' = \frac{2b}{2c} = \frac{b}{c}$,
通过比较可以看出,新的正弦值和余弦值与原始的正弦值和余弦值相等,即锐角$A$的正弦值和余弦值都没有变化。
【答案】:
A.都没有变化。
本题主要考察锐角三角比的意义,特别是在直角三角形中,当各边长度发生变化时,锐角的正弦值和余弦值会如何变化。
在直角三角形中,锐角的正弦值定义为对边长度与斜边长度的比值,余弦值定义为邻边长度与斜边长度的比值。
设原始直角三角形$ABC$中,角$A$为锐角,对边$BC=a$,邻边$AC=b$,斜边$AB=c$。
根据正弦和余弦的定义,有:
$\sin A = \frac{a}{c}$,
$\cos A = \frac{b}{c}$,
当各边长度都扩大2倍时,新的对边长度为$2a$,新的邻边长度为$2b$,新的斜边长度为$2c$。
此时,新的正弦值和余弦值为:
$\sin A' = \frac{2a}{2c} = \frac{a}{c}$,
$\cos A' = \frac{2b}{2c} = \frac{b}{c}$,
通过比较可以看出,新的正弦值和余弦值与原始的正弦值和余弦值相等,即锐角$A$的正弦值和余弦值都没有变化。
【答案】:
A.都没有变化。
5. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,如果$AC = 5$,$AB = 13$,那么$sinA = $
$\frac{12}{13}$
.
答案:
【解析】:
本题考查的是锐角三角函数的定义及运用。在直角三角形中,$\sin$的定义是对边长除以斜边长。
已知在$Rt \bigtriangleup ABC$中,$\angle C = 90^{\circ}$,$AC = 5$,$AB = 13$。
我们需要求$\sin A$,根据$\sin$的定义,$\sin A = \frac{BC}{AB}$。
但题目没有直接给出$BC$的长度,我们需要先通过勾股定理求出$BC$。
勾股定理公式为$AB^2 = AC^2 + BC^2$,
所以,$BC = \sqrt{AB^2 - AC^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12$。
然后,我们可以求出$\sin A = \frac{BC}{AB} = \frac{12}{13}$。
【答案】:
$\frac{12}{13}$
本题考查的是锐角三角函数的定义及运用。在直角三角形中,$\sin$的定义是对边长除以斜边长。
已知在$Rt \bigtriangleup ABC$中,$\angle C = 90^{\circ}$,$AC = 5$,$AB = 13$。
我们需要求$\sin A$,根据$\sin$的定义,$\sin A = \frac{BC}{AB}$。
但题目没有直接给出$BC$的长度,我们需要先通过勾股定理求出$BC$。
勾股定理公式为$AB^2 = AC^2 + BC^2$,
所以,$BC = \sqrt{AB^2 - AC^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12$。
然后,我们可以求出$\sin A = \frac{BC}{AB} = \frac{12}{13}$。
【答案】:
$\frac{12}{13}$
6. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,$BC = 8$,$AB = 10$.若点$G是△ABC$的重心,则$cos∠GCB = $
$\frac{4}{5}$
.
答案:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$BC=8$,$AB=10$,
$\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-8^{2}}=6$。
取$AB$中点$D$,连接$CD$,则$CD=\frac{1}{2}AB=5$,$D$为$AB$中点。
$\because G$是$\triangle ABC$重心,$\therefore CG=\frac{2}{3}CD=\frac{10}{3}$,$DG=\frac{1}{3}CD=\frac{5}{3}$。
过$G$作$GE\perp BC$于$E$,过$D$作$DF\perp BC$于$F$,则$DF// AC$,$DF=\frac{1}{2}AC=3$。
$\because GE// DF$,$\frac{CG}{CD}=\frac{2}{3}$,$\therefore GE=\frac{2}{3}DF=2$。
在$Rt\triangle GEC$中,$CE=\sqrt{CG^{2}-GE^{2}}=\sqrt{(\frac{10}{3})^{2}-2^{2}}=\frac{8}{3}$。
$\therefore \cos\angle GCB=\frac{CE}{CG}=\frac{\frac{8}{3}}{\frac{10}{3}}=\frac{4}{5}$。
$\frac{4}{5}$
$\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-8^{2}}=6$。
取$AB$中点$D$,连接$CD$,则$CD=\frac{1}{2}AB=5$,$D$为$AB$中点。
$\because G$是$\triangle ABC$重心,$\therefore CG=\frac{2}{3}CD=\frac{10}{3}$,$DG=\frac{1}{3}CD=\frac{5}{3}$。
过$G$作$GE\perp BC$于$E$,过$D$作$DF\perp BC$于$F$,则$DF// AC$,$DF=\frac{1}{2}AC=3$。
$\because GE// DF$,$\frac{CG}{CD}=\frac{2}{3}$,$\therefore GE=\frac{2}{3}DF=2$。
在$Rt\triangle GEC$中,$CE=\sqrt{CG^{2}-GE^{2}}=\sqrt{(\frac{10}{3})^{2}-2^{2}}=\frac{8}{3}$。
$\therefore \cos\angle GCB=\frac{CE}{CG}=\frac{\frac{8}{3}}{\frac{10}{3}}=\frac{4}{5}$。
$\frac{4}{5}$
7. 在$Rt△ABC$中,已知$∠C = 90^{\circ}$,$cosA= \frac{3}{5}$,则$sinA$的值是
$\frac{4}{5}$
.
答案:
【解析】:
本题主要考查三角函数的基本性质,特别是在直角三角形中,两个锐角的正弦和余弦之间的关系。
在$Rt \bigtriangleup ABC$中,由于$\angle C = 90^\circ$,$cosA$定义为邻边与斜边的比值,即$cosA = \frac{AC}{AB} = \frac{3}{5}$。
设$AC = 3x$,$AB = 5x$($x > 0$),利用勾股定理,可以求出对边$BC$的长度:
$BC = \sqrt{AB^2 - AC^2} = \sqrt{(5x)^2 - (3x)^2} = \sqrt{25x^2 - 9x^2} = \sqrt{16x^2} = 4x$,
因此,$sinA$,作为对边与斜边的比值,可以计算为:
$sinA = \frac{BC}{AB} = \frac{4x}{5x} = \frac{4}{5}$。
【答案】:
$\frac{4}{5}$
本题主要考查三角函数的基本性质,特别是在直角三角形中,两个锐角的正弦和余弦之间的关系。
在$Rt \bigtriangleup ABC$中,由于$\angle C = 90^\circ$,$cosA$定义为邻边与斜边的比值,即$cosA = \frac{AC}{AB} = \frac{3}{5}$。
设$AC = 3x$,$AB = 5x$($x > 0$),利用勾股定理,可以求出对边$BC$的长度:
$BC = \sqrt{AB^2 - AC^2} = \sqrt{(5x)^2 - (3x)^2} = \sqrt{25x^2 - 9x^2} = \sqrt{16x^2} = 4x$,
因此,$sinA$,作为对边与斜边的比值,可以计算为:
$sinA = \frac{BC}{AB} = \frac{4x}{5x} = \frac{4}{5}$。
【答案】:
$\frac{4}{5}$
8. 如图,已知点$P的坐标是(a,b)$,则:
$\frac{∠α的对边}{∠α的邻边}= $
$\frac{∠α的对边}{∠α的斜边}= $

$\frac{∠α的对边}{∠α的邻边}= $
$\frac{b}{a}$
;$\frac{∠α的邻边}{∠α的对边}= $$\frac{a}{b}$
;$\frac{∠α的对边}{∠α的斜边}= $
$\frac{b}{\sqrt{a^{2}+b^{2}}}$
;$\frac{∠α的邻边}{∠α的斜边}= $$\frac{a}{\sqrt{a^{2}+b^{2}}}$
.
答案:
【解析】:
本题主要考查在直角坐标系中结合三角函数的定义,根据已知点的坐标求三角函数值,关键在于明确在直角三角形中各边的名称以及三角函数的定义。
在以点$P(a,b)$构成的直角三角形中,对于角$\alpha$,它的对边是点$P$的纵坐标$b$所对应的边,邻边是点$P$的横坐标$a$所对应的边,斜边是点$P$到原点的距离$\sqrt{a^{2}+b^{2}}$。
根据正切函数的定义:在直角三角形中,一个锐角的正切值等于它的对边与邻边的比值,所以$\frac{\angle\alpha的对边}{\angle\alpha的邻边}=\frac{b}{a}$。
根据余切函数的定义:在直角三角形中,一个锐角的余切值等于它的邻边与对边的比值,所以$\frac{\angle\alpha的邻边}{\angle\alpha的对边}=\frac{a}{b}$。
根据正弦函数的定义:在直角三角形中,一个锐角的正弦值等于它的对边与斜边的比值,所以$\frac{\angle\alpha的对边}{\angle\alpha的斜边}=\frac{b}{\sqrt{a^{2}+b^{2}}}$。
根据余弦函数的定义:在直角三角形中,一个锐角的余弦值等于它的邻边与斜边的比值,所以$\frac{\angle\alpha的邻边}{\angle\alpha的斜边}=\frac{a}{\sqrt{a^{2}+b^{2}}}$。
【答案】:
$\frac{b}{a}$;$\frac{a}{b}$;$\frac{b}{\sqrt{a^{2}+b^{2}}}$;$\frac{a}{\sqrt{a^{2}+b^{2}}}$
本题主要考查在直角坐标系中结合三角函数的定义,根据已知点的坐标求三角函数值,关键在于明确在直角三角形中各边的名称以及三角函数的定义。
在以点$P(a,b)$构成的直角三角形中,对于角$\alpha$,它的对边是点$P$的纵坐标$b$所对应的边,邻边是点$P$的横坐标$a$所对应的边,斜边是点$P$到原点的距离$\sqrt{a^{2}+b^{2}}$。
根据正切函数的定义:在直角三角形中,一个锐角的正切值等于它的对边与邻边的比值,所以$\frac{\angle\alpha的对边}{\angle\alpha的邻边}=\frac{b}{a}$。
根据余切函数的定义:在直角三角形中,一个锐角的余切值等于它的邻边与对边的比值,所以$\frac{\angle\alpha的邻边}{\angle\alpha的对边}=\frac{a}{b}$。
根据正弦函数的定义:在直角三角形中,一个锐角的正弦值等于它的对边与斜边的比值,所以$\frac{\angle\alpha的对边}{\angle\alpha的斜边}=\frac{b}{\sqrt{a^{2}+b^{2}}}$。
根据余弦函数的定义:在直角三角形中,一个锐角的余弦值等于它的邻边与斜边的比值,所以$\frac{\angle\alpha的邻边}{\angle\alpha的斜边}=\frac{a}{\sqrt{a^{2}+b^{2}}}$。
【答案】:
$\frac{b}{a}$;$\frac{a}{b}$;$\frac{b}{\sqrt{a^{2}+b^{2}}}$;$\frac{a}{\sqrt{a^{2}+b^{2}}}$
9. 如果$α$是锐角,且$cosα= \frac{4}{5}$,那么$sin(90^{\circ} - α)$的值等于
$\frac{4}{5}$
.
答案:
【解析】:
本题主要考查三角函数的诱导公式以及三角函数的基本性质。
根据三角函数的诱导公式,对于任意角度$α$,都有$\sin(90^{\circ} - α) = \cosα$。
题目已给出$\cosα = \frac{4}{5}$,且$α$是锐角,所以可以直接将$\cosα$的值代入诱导公式中求解$\sin(90^{\circ} - α)$。
【答案】:
$\sin(90^{\circ} - α) = \cosα = \frac{4}{5}$。
故答案为:$\frac{4}{5}$。
本题主要考查三角函数的诱导公式以及三角函数的基本性质。
根据三角函数的诱导公式,对于任意角度$α$,都有$\sin(90^{\circ} - α) = \cosα$。
题目已给出$\cosα = \frac{4}{5}$,且$α$是锐角,所以可以直接将$\cosα$的值代入诱导公式中求解$\sin(90^{\circ} - α)$。
【答案】:
$\sin(90^{\circ} - α) = \cosα = \frac{4}{5}$。
故答案为:$\frac{4}{5}$。
10. 如图,两条宽度都为1的纸条交叉重叠放在一起,且它们的夹角为$α$,则它们重叠部分(图中阴影部分)的面积为
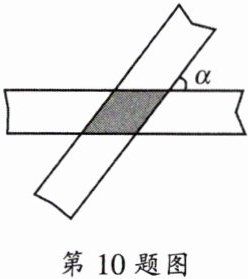
$\frac{1}{\sin\alpha}$
.
答案:
【解析】:
本题主要考查三角函数的应用以及平行四边形的面积公式,需要利用三角函数求出重叠部分平行四边形的高,再结合平行四边形的底和面积公式求解。
观察图形可知,重叠部分是一个平行四边形。
已知纸条宽度为$1$,即平行四边形的高为$1$。
因为两条纸条的夹角为$\alpha$,根据三角函数的定义,在由高、斜边(纸条的一边)和夹角$\alpha$构成的直角三角形中,$\sin\alpha$等于对边(高)与斜边的比值,所以平行四边形的底边长为$\frac{1}{\sin\alpha}$。
根据平行四边形的面积公式$S = 底×高$,将底$\frac{1}{\sin\alpha}$和高$1$代入公式,可得重叠部分的面积$S = \frac{1}{\sin\alpha}×1=\frac{1}{\sin\alpha}$。
【答案】:$\frac{1}{\sin\alpha}$
本题主要考查三角函数的应用以及平行四边形的面积公式,需要利用三角函数求出重叠部分平行四边形的高,再结合平行四边形的底和面积公式求解。
观察图形可知,重叠部分是一个平行四边形。
已知纸条宽度为$1$,即平行四边形的高为$1$。
因为两条纸条的夹角为$\alpha$,根据三角函数的定义,在由高、斜边(纸条的一边)和夹角$\alpha$构成的直角三角形中,$\sin\alpha$等于对边(高)与斜边的比值,所以平行四边形的底边长为$\frac{1}{\sin\alpha}$。
根据平行四边形的面积公式$S = 底×高$,将底$\frac{1}{\sin\alpha}$和高$1$代入公式,可得重叠部分的面积$S = \frac{1}{\sin\alpha}×1=\frac{1}{\sin\alpha}$。
【答案】:$\frac{1}{\sin\alpha}$
查看更多完整答案,请扫码查看


