《2025年通城学典课时作业本九年级数学全一册浙教版》

1. 计算:$2\sin 60^{\circ }+3\tan 30^{\circ }=$$2\sqrt{3}$.

答案： $2\sqrt{3}$

2. (易错题)(2024·达州)如图,在由8个全等的菱形组成的网格中,每个小菱形的边长均为2,$\angle ABD= 120^{\circ }$,其中点A,B,C都在格点上,则$\tan \angle BCD$的值为(B)
A.2
B.$2\sqrt {3}$
C.$\frac {3}{2}$
D.3

答案： B [易错分析]巧用菱形的对角线平分一组对角的性质，延长 BC 与网格的边相交，从而构建直角三角形，切忌凭直觉得出BC⊥AD的错误结论.

3. 如图,在$\text{Rt}\triangle ACB$中,$AC= 1,\angle C= 90^{\circ },\angle ABC= 30^{\circ }$,延长CB至点D,使$BD= AB$,连结AD,得$\angle D= 15^{\circ }$,那么$\tan 15^{\circ }=\frac {AC}{CD}= \frac {1}{2+\sqrt {3}}= \frac {2-\sqrt {3}}{(2+\sqrt {3})× (2-\sqrt {3})}= 2-\sqrt {3}$.

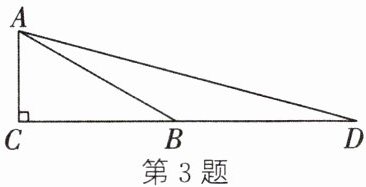
类比这种方法,计算$\tan 22.5^{\circ }$的值为(B)
A.$\sqrt {2}+1$
B.$\sqrt {2}-1$
C.$\sqrt {2}$
D.$\frac {1}{2}$

答案： B

4. 在$\triangle ABC$中,$\angle C= 90^{\circ }$.若$\tan A= \frac {\sqrt {3}}{3}$,则$\cos B$的值为$\frac{1}{2}$.

答案： $\frac{1}{2}$

5. 如图,在$\triangle ABC$中,$AB= 5,BC= 2,\sin B= \frac {3}{5}$,则AC的长为(B)
A.3
B.$\sqrt {13}$
C.$2\sqrt {3}$
D.4

答案： B

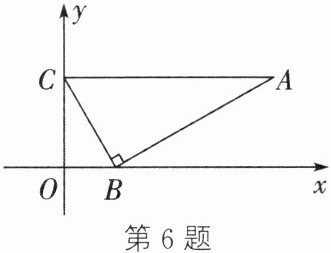
6. 如图,$\triangle ABC$的顶点B,C的坐标分别为$(1,0),(0,\sqrt {3})$,且$\angle ABC= 90^{\circ },\angle A= 30^{\circ }$,则顶点A的坐标为______$(4,\sqrt{3})$.

答案： $(4,\sqrt{3})$