第14页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
利用解一元二次方程可求二次函数的图象与横轴(或平行于横轴的直线)的
交点坐标
;反过来,也可以利用二次函数的图象求一元二次方程的解
.
答案:
交点坐标 解
1. 小李在求一元二次方程$-2x^{2}+4x+1= 0$的近似解时,先在平面直角坐标系中使用软件绘制了二次函数$y= -2x^{2}+4x+1$的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程的两个解的取值范围是$-1<x_{1}<0$,$2<x_{2}<3$.小李的这种方法主要运用的数学思想是(

A.分类讨论思想
B.类比思想
C.数形结合思想
D.建模思想
C
)
A.分类讨论思想
B.类比思想
C.数形结合思想
D.建模思想
答案:
C
2. 已知二次函数$y= x^{2}+5x-3$,y与x的部分对应值如下表(y的值精确到0.01):
| x | 0 | 0.25 | 0.5 | 0.75 | 1 |
| y | -3.00 | -1.69 | -0.25 | 1.31 | 3.00 |
则方程$x^{2}+5x-3= 0$的一个解x的取值范围是(
A.$0<x<0.25$
B.$0.25<x<0.5$
C.$0.5<x<0.75$
D.$0.75<x<1$
| x | 0 | 0.25 | 0.5 | 0.75 | 1 |
| y | -3.00 | -1.69 | -0.25 | 1.31 | 3.00 |
则方程$x^{2}+5x-3= 0$的一个解x的取值范围是(
C
)A.$0<x<0.25$
B.$0.25<x<0.5$
C.$0.5<x<0.75$
D.$0.75<x<1$
答案:
C
3. 若抛物线$y= x^{2}+2x+m$与y轴交点的纵坐标为-3,则该抛物线与x轴的两个交点的坐标分别为
(1,0),(-3,0)
.
答案:
(1,0),(-3,0)
4. (2024·龙泉期中)在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析(如图),发现实心球飞行高度y(米)与水平距离x(米)之间的表达式为$y= -\frac {1}{10}x^{2}+\frac {3}{5}x+\frac {8}{5}$,由此可知小宇此次实心球训练的成绩为

8
米.
答案:
8
5. 已知抛物线$y= -x^{2}+bx+c$的顶点坐标为(1,5),且关于x的一元二次方程$x^{2}-bx-c= m$有两个相等的实数根,则m的值为
-5
.
答案:
-5
6. (1)请在如图所示的平面直角坐标系中画出二次函数$y= x^{2}-2x$的大致图象;
(2)根据方程的解与函数图象的关系,将方程$x^{2}-2x= 1$的解在图上表示出来;
(3)观察图象,直接写出方程$x^{2}-2x= 1$的解(结果精确到0.1).

(2)根据方程的解与函数图象的关系,将方程$x^{2}-2x= 1$的解在图上表示出来;
(3)观察图象,直接写出方程$x^{2}-2x= 1$的解(结果精确到0.1).

答案:
(1)如图所示 (2)如图,点M,N的横坐标即为所求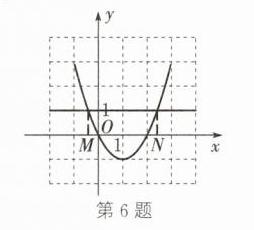
(3)$x_{1}\approx -0.4$,$x_{2}\approx$2.4
(1)如图所示 (2)如图,点M,N的横坐标即为所求

(3)$x_{1}\approx -0.4$,$x_{2}\approx$2.4
查看更多完整答案,请扫码查看


