《2025年通城学典课时作业本九年级数学全一册浙教版》

10. 如图,E 是线段 BC 的中点,∠B= ∠C= ∠AED,则下列结论不一定正确的是(D)
A.△ABE 与△ECD 相似
B.△ABE 与△AED 相似
C.$\frac{AB}{AE}= \frac{AE}{AD}$
D.∠BAE= ∠ADE

答案： D

11. (2023·东营)如图,△ABC 为等边三角形,点 D,E 分别在边 BC,AB 上,∠ADE= 60°. 若 BD= 4DC,DE= 2.4,则 AD 的长为 (C)

A.1.8
B.2.4
C.3
D.3.2

答案： C　解析:
∵$\triangle ABC$为等边三角形，
∴$AC = BC$，$\angle B = \angle C = 60^{\circ}$。
∵$\angle ADB = \angle ADE + \angle BDE = \angle C + \angle CAD$，$\angle ADE = 60^{\circ}$，
∴$\angle BDE = \angle CAD$。
∴$\triangle ADC \sim \triangle DEB$。
∴$\frac{AD}{DE} = \frac{AC}{DB}$。
∵$BD = 4DC$，
∴$BD = \frac{4}{5}BC$。
∴$\frac{AD}{DE} = \frac{AC}{DB} = \frac{BC}{\frac{4}{5}BC} = \frac{5}{4}$。
∵$DE = 2.4$，
∴$AD = \frac{5}{4}DE = 3$。

12. 如图,在△ABC 中,AB= AC= 6,∠BAC= 120°,D 是 BC 的中点,边 AB 上有一点 E,CA 的延长线上有一点 F,且∠EDF= ∠C. 若 BE= 4,则 CF= $\frac{27}{4}$.

答案： $\frac{27}{4}$

13. 定义：在△ABC 中,D,E,F 分别是边 AB,BC,CA 上的动点,若△DEF∽△ABC,则称△DEF 是△ABC 的“子三角形”.
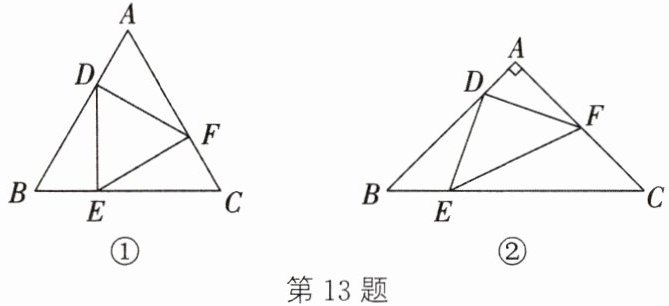
(1)如图①,△ABC 是等边三角形,D,E,F 分别是边 AB,BC,CA 上的动点,且 AD= BE= CF. 求证：△DEF 是△ABC 的“子三角形”.
(2)如图②,在△ABC 中,AB= AC,∠A= 90°,△DEF 是△ABC 的“子三角形”. 若 BE= $\sqrt{2}$,求 CF 和 AD 的长.

答案：
(1)
∵$\triangle ABC$是等边三角形，
∴$AB = BC = AC$，$\angle A = \angle B = \angle C = 60^{\circ}$。
∵$AD = BE = CF$，
∴$AC - CF = AB - AD = BC - BE$，即$AF = BD = CE$。
∴易得$\triangle DAF \cong \triangle EBD \cong \triangle FCE$。
∴$DF = ED = FE$。
∴$\triangle DEF$是等边三角形。
∴$\angle DEF = \angle EDF = \angle B = \angle A = 60^{\circ}$。
∴$\triangle DEF \sim \triangle ABC$。
∴$\triangle DEF$是$\triangle ABC$的“子三角形”。
(2)过点E作$EH \perp AB$于点H，则$\angle DHE = 90^{\circ}$。
∵$AB = AC$，$\angle A = 90^{\circ}$，
∴$\angle B = \angle C = 45^{\circ}$。
∵$\triangle DEF$是$\triangle ABC$的“子三角形”，
∴$\triangle DEF \sim \triangle ABC$。
∴易得$\angle DEF = \angle B = 45^{\circ}$，$DE = FD$，$\angle EDF = 90^{\circ}$。
∴$\angle ADF + \angle HDE = 90^{\circ}$。在$Rt\triangle DEF$中，由勾股定理，易得$EF = \sqrt{2}DE$。
∵$\angle A = 90^{\circ}$，
∴$\angle ADF + \angle AFD = 90^{\circ}$，
∴$\angle HDE = \angle AFD$。在$\triangle DEH$和$\triangle FDA$中，$\begin{cases} \angle DHE = \angle A \\ \angle HDE = \angle AFD \\ DE = FD \end{cases}$，
∴$\triangle DEH \cong \triangle FDA$。
∴$HE = AD$。
∵易知$\triangle BEH$是等腰直角三角形，又
∵$BE = \sqrt{2}$，
∴易得$HE = 1$。
∴$AD = 1$。
∵$\angle DEC = \angle DEF + \angle CEF = \angle B + \angle BDE$，$\angle B = \angle DEF$，
∴$\angle BDE = \angle CEF$。又
∵$\angle B = \angle C$，
∴$\triangle BDE \sim \triangle CEF$。
∴$\frac{BE}{CF} = \frac{DE}{EF} = \frac{DE}{\sqrt{2}DE} = \frac{\sqrt{2}}{2}$。
∴$CF = 2$