第38页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为l=
$\frac{n\pi R}{180}$
. 弧长不仅与所对的圆心角的度数
有关,还与半径的长度
有关.
答案:
$\frac{n\pi R}{180}$ 度数 长度
1. (教材P103课内练习第1题变式)(2024·贵州)如图,在扇形纸扇中,∠AOB= 150°. 若OA= 24,则$\overset{\frown}{AB}$的长为(
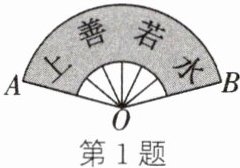
A.30π
B.25π
C.20π
D.10π
C
)
A.30π
B.25π
C.20π
D.10π
答案:
C
2. 若一条弧所对的圆心角为135°,弧长等于半径为3 cm的圆的周长的5倍,则这条弧所在圆的半径为(
A.45 cm
B.40 cm
C.35 cm
D.30 cm
B
)A.45 cm
B.40 cm
C.35 cm
D.30 cm
答案:
B
3. (2024·包头)如图,在扇形AOB中,∠AOB= 80°,半径OA= 3,C是$\overset{\frown}{AB}$上一点,连结OC,D是OC上一点,且OD= DC,连结BD. 若BD⊥OC,则$\overset{\frown}{AC}$的长为(
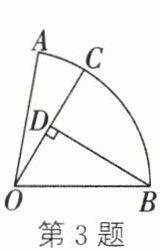
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.π
B
)
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.π
答案:
B
4. 半径为5 cm的圆的内接正五边形的一边所对劣弧的长为
$2\pi$
cm.
答案:
$2\pi$
5. 如图,点A,B,C在半径为9的⊙O上,$\overset{\frown}{AB}$的长为2π,则∠ACB的度数为
$20^{\circ}$
.
答案:
$20^{\circ}$
6. 如图,⊙O的半径为15 m,A,B是⊙O上两点,且∠AOB= 120°,则$\overset{\frown}{AB}$的长为
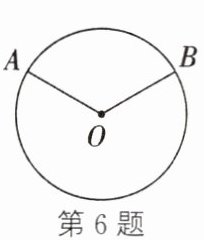
$10\pi$
m(结果保留π).
答案:
$10\pi$
7. (2024·杭州拱墅模拟)如图,在△ABC中,以BC为直径的半圆O分别与AB,AC交于点D,E. 若BC= 6,∠A= 60°,则$\overset{\frown}{DE}$的长为
$\pi$
.
答案:
$\pi$
8. 如图,AB是半圆O的直径,AB= 6,弦CD的长为3,$\overset{\frown}{AD}的长为\frac{3\pi}{4}$,求$\overset{\frown}{BC}$的长.
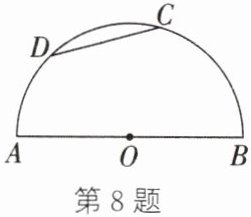

答案:
连结OD,OC.
∵ AB是半圆O的直径,AB=6,弦CD的长为3,
∴ CD=OC=OD=3.
∴ △CDO是等边三角形.
∴ $\angle COD=60^{\circ}$.
∴ $\overset{\frown}{CD}$的长为$\frac{60×\pi×3}{180}=\pi$.又
∵ 半圆弧的长为$\frac{1}{2}×6\pi=3\pi$,
∴ $\overset{\frown}{BC}$的长为$3\pi - \pi - \frac{3\pi}{4}=\frac{5\pi}{4}$
∵ AB是半圆O的直径,AB=6,弦CD的长为3,
∴ CD=OC=OD=3.
∴ △CDO是等边三角形.
∴ $\angle COD=60^{\circ}$.
∴ $\overset{\frown}{CD}$的长为$\frac{60×\pi×3}{180}=\pi$.又
∵ 半圆弧的长为$\frac{1}{2}×6\pi=3\pi$,
∴ $\overset{\frown}{BC}$的长为$3\pi - \pi - \frac{3\pi}{4}=\frac{5\pi}{4}$
查看更多完整答案,请扫码查看


