第13页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
6. (2024·诸暨段考)某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园的面积尽可能大,同学们提出了围成如图所示的矩形、等腰三角形(底边靠墙)、半圆形这三种方案,最佳方案是(
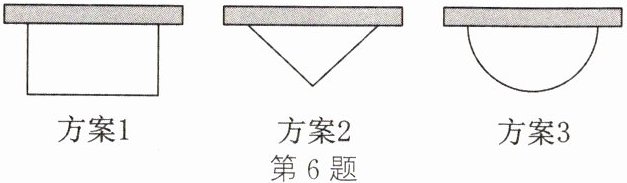
A.方案1
B.方案2
C.方案3
D.面积都一样
C
)
A.方案1
B.方案2
C.方案3
D.面积都一样
答案:
C
7. 如图,在边长为6 cm的正方形ABCD中,点E,F,G,H分别从点A,B,C,D同时出发,均以1 cm/s的速度分别向点B,C,D,A匀速运动,当点E到达点B时,四个点同时停止运动.在运动过程中,当运动时间为
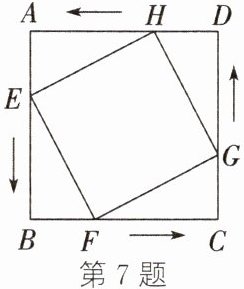
3
s时,四边形EFGH的面积最小,最小面积为18
$ cm^2.$
答案:
3 18
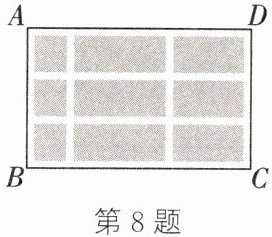
8. (教材P25作业题第3题变式)如图,矩形ABCD是一个月季养植园,AD= 32米,AB= 20米.为了便于养护与运输,养植园内留有四横四纵等宽道路,养植面积与道路面积之比为7:3.
(1)求道路的宽度.
(2)养植区域内月季小盆栽要均匀摆放,即每平方米摆放的盆数一样.每平方米最多能摆放36盆,密度越大,花的品质会下降,每盆月季的出售价也会随之降低.养植区域内现在每平方米有月季小盆栽10盆,每盆的出售价为5元.分析发现:每平方米每增加5盆,每盆的出售价会下降0.5元.老板准备增加养植数量,以获得最多的出售总额,那么每平方米应该摆放多少盆月季小盆栽才能使出售总额最多?
(1)求道路的宽度.
(2)养植区域内月季小盆栽要均匀摆放,即每平方米摆放的盆数一样.每平方米最多能摆放36盆,密度越大,花的品质会下降,每盆月季的出售价也会随之降低.养植区域内现在每平方米有月季小盆栽10盆,每盆的出售价为5元.分析发现:每平方米每增加5盆,每盆的出售价会下降0.5元.老板准备增加养植数量,以获得最多的出售总额,那么每平方米应该摆放多少盆月季小盆栽才能使出售总额最多?

答案:
(1)$S_{矩形ABCD}= 32×20 = 640$(平方米),$S_{道路面积}= 640×\frac{3}{7 + 3}= 192$(平方米).把养殖区域放在一起,如图,设道路的宽度为a米,则$4a×20 + 4a×32 - (4a)^{2}= 192$,化简,得$(a - 1)(a - 12)= 0$,解得a = 1或a = 12.若a = 12,则$4a = 48 > 32$,故a = 12不符合题意.
∴道路的宽度为1米 (2)设每平方米增加5x盆月季小盆栽,每平方米月季小盆栽的出售总额为y元.根据题意,得$y = (10 + 5x)(5 - 0.5x)$,化简,得$y = -2.5(x - 4)^{2}+90$.
∵$10 < 10 + 5x ≤ 36$,
∴$0 < x ≤ 5.2$.又
∵$-2.5 < 0$,
∴当x = 4时,y取最大值.此时$10 + 5×4 = 30$(盆).
∴每平方米应该摆放30盆月季小盆栽才能使出售总额最多
∴道路的宽度为1米 (2)设每平方米增加5x盆月季小盆栽,每平方米月季小盆栽的出售总额为y元.根据题意,得$y = (10 + 5x)(5 - 0.5x)$,化简,得$y = -2.5(x - 4)^{2}+90$.
∵$10 < 10 + 5x ≤ 36$,
∴$0 < x ≤ 5.2$.又
∵$-2.5 < 0$,
∴当x = 4时,y取最大值.此时$10 + 5×4 = 30$(盆).
∴每平方米应该摆放30盆月季小盆栽才能使出售总额最多
9. (2023·株洲)如图,在平面直角坐标系中,四边形OABC为正方形,其中点A,C分别在x轴的负半轴和y轴的负半轴上,点B在第三象限内,点A的坐标为(t,0),点P(1,2)在函数y= k/x(k>0,x>0)的图象上.
(1)求k的值;
(2)连结BP,CP,记△BCP的面积为S,设$T= 2S-2t^2,$求T的最大值.
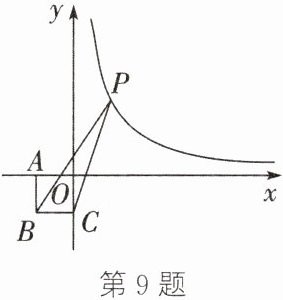
(1)求k的值;
(2)连结BP,CP,记△BCP的面积为S,设$T= 2S-2t^2,$求T的最大值.

答案:
(1)
∵点P(1,2)在函数$y = \frac{k}{x}(k > 0,x > 0)$的图象上,
∴$2 = \frac{k}{1}$.
∴k = 2 (2)
∵点A(t,0)在x轴的负半轴上,
∴$OA = -t$,$t < 0$.
∵四边形OABC为正方形,
∴$OC = BC = OA = -t$,$BC// x$轴.
∴$S = \frac{1}{2}×(-t)×(2 - t)=\frac{1}{2}t^{2}-t$.
∴$T = 2S - 2t^{2}= 2(\frac{1}{2}t^{2}-t)-2t^{2}=-t^{2}-2t = -(t + 1)^{2}+1$.
∵$-1 < 0$,$t < 0$,
∴当t = -1时,T有最大值,为1
∵点P(1,2)在函数$y = \frac{k}{x}(k > 0,x > 0)$的图象上,
∴$2 = \frac{k}{1}$.
∴k = 2 (2)
∵点A(t,0)在x轴的负半轴上,
∴$OA = -t$,$t < 0$.
∵四边形OABC为正方形,
∴$OC = BC = OA = -t$,$BC// x$轴.
∴$S = \frac{1}{2}×(-t)×(2 - t)=\frac{1}{2}t^{2}-t$.
∴$T = 2S - 2t^{2}= 2(\frac{1}{2}t^{2}-t)-2t^{2}=-t^{2}-2t = -(t + 1)^{2}+1$.
∵$-1 < 0$,$t < 0$,
∴当t = -1时,T有最大值,为1
查看更多完整答案,请扫码查看


