第28页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 垂径定理的逆定理
(1)定理 1:平分弦(不是直径)的直径垂直于弦,并且平分
(2)定理 2:平分弧的直径
(1)定理 1:平分弦(不是直径)的直径垂直于弦,并且平分
弦所对的弧
.(2)定理 2:平分弧的直径
垂直平分
弧所对的弦.
答案:
1.
(1)弦所对的弧
(2)垂直平分
(1)弦所对的弧
(2)垂直平分
2. 垂径定理的解读:(1) 过圆心;(2) 平分弦(不是直径);(3) 垂直于弦;(4) 平分弦所对的优弧;(5) 平分弦所对的劣弧.若一条直线具备这五项中任意
两
项,则必具备另外三
项.
答案:
两 三
1.(2023·宜昌)如图,OA,OB,OC 都是$\odot O$的半径,AC,OB 交于点 D.若$AD= CD= 8$,$OD= 6$,则 BD 的长为(
A.5
B.4
C.3
D.2
B
)A.5
B.4
C.3
D.2
答案:
B
2. 如图,$\odot O$的半径为 2 cm,弦 AB 的长为$2\sqrt {3}cm$,则这条弦的中点 C 到弦所对劣弧的中点 D 的距离为(
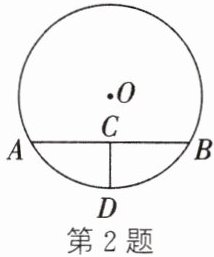
A.1 cm
B.2 cm
C.$\sqrt {2}cm$
D.$\sqrt {3}cm$
A
)
A.1 cm
B.2 cm
C.$\sqrt {2}cm$
D.$\sqrt {3}cm$
答案:
A
3. 如图,$\odot O$的半径为 4,弦$AB= 4\sqrt {3}$,E 为$\widehat {AB}$的中点,OE 交 AB 于点 F,则 OF 的长为(
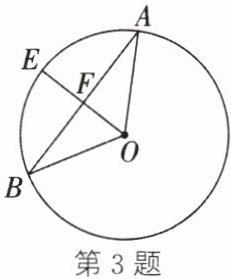
A.1
B.$2\sqrt {3}$
C.2
D.$2\sqrt {2}$
C
)
A.1
B.$2\sqrt {3}$
C.2
D.$2\sqrt {2}$
答案:
C
4. 如图,AB,CD 是$\odot O$的直径,D 是$\widehat {AE}$的中点,AE 与 CD 交于点 F.若$OF= 3$,则 BE 的长为
6
.
答案:
6
5.(2024·长沙改编)在$\odot O$中,弦 AB 的长为8,E 为 AB 的中点,且 OE 的长为 4,则$\odot O$的半径为
$4\sqrt{2}$
.
答案:
$4\sqrt{2}$
6. 如图,$\odot O$的弦 AB 的长为半径 OA 的$\sqrt {3}$倍,C 是$\widehat {AB}$的中点,AB,OC 交于点 P.求证:四边形 OACB 是菱形.
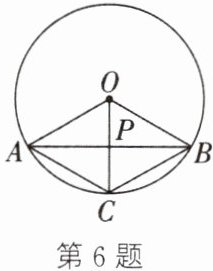

答案:
在$\odot O$中,$\because$ C是$\widehat{AB}$的中点,$\therefore \widehat{AC}=\widehat{BC}$. $\therefore OC\perp AB$,$PA=PB$. 又$\because AB=\sqrt{3}OA$,$\therefore AP=\frac{\sqrt{3}}{2}OA$. 设$OA=r$,则$AP=\frac{\sqrt{3}}{2}r$. 在$Rt\triangle APO$中,由勾股定理,得$OP=\sqrt{OA^2 - AP^2}=\frac{1}{2}r$,即$OP=\frac{1}{2}OA$,$\therefore OP=\frac{1}{2}OC$,即$OP=CP$. $\because PA=PB$,$\therefore$ 四边形OACB是平行四边形. 又$\because OA=OB$,$\therefore$ 四边形OACB是菱形
查看更多完整答案,请扫码查看


