第45页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
7. (2024·杭州西湖段考)黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,取正方形ABCD的底边BC的中点E,以点E为圆心,线段DE的长为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形.若$CF= 4a$,则AB的长为(
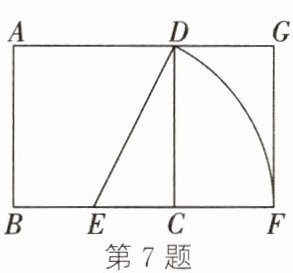
A.$(\sqrt{5}-1)a$
B.$(2\sqrt{5}-2)a$
C.$(\sqrt{5}+1)a$
D.$(2\sqrt{5}+2)a$
D
)
A.$(\sqrt{5}-1)a$
B.$(2\sqrt{5}-2)a$
C.$(\sqrt{5}+1)a$
D.$(2\sqrt{5}+2)a$
答案:
D
8. 如图,在五角星中,$AD= BC$,C,D都是AB的黄金分割点,且$AB= 3$,则$CD= $
$3\sqrt{5}-6$
.
答案:
$3\sqrt{5}-6$
9. 如图,以线段AB为一边作正方形ABCD,取AD的中点E,连结EB,延长DA到点F,使$EF= EB$,以线段AF为一边作正方形AFGH,点H在边AB上.试判断H是否为线段AB的黄金分割点,并说明理由.
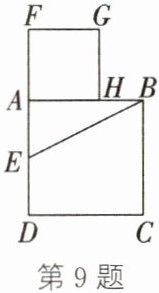

答案:
是 理由:设正方形ABCD的边长为2a.
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB=2a.
∵E是AD的中点,
∴$AE=\frac{1}{2}AD=a$.在Rt△AEB中,$EB=\sqrt{AB^2+AE^2}=\sqrt{5}a$.
∵四边形AFGH是正方形,
∴AH=AF=EF-AE=EB-AE=$(\sqrt{5}-1)a$.
∴HB=AB-AH=$(3-\sqrt{5})a$,$AH^2=(6-2\sqrt{5})a^2$.
∴$AB\cdot HB=2a\times(3-\sqrt{5})a=(6-2\sqrt{5})a^2$.
∴$AH^2=AB\cdot HB$,即$\frac{AH}{AB}=\frac{HB}{AH}$.
∴H是线段AB的黄金分割点.
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB=2a.
∵E是AD的中点,
∴$AE=\frac{1}{2}AD=a$.在Rt△AEB中,$EB=\sqrt{AB^2+AE^2}=\sqrt{5}a$.
∵四边形AFGH是正方形,
∴AH=AF=EF-AE=EB-AE=$(\sqrt{5}-1)a$.
∴HB=AB-AH=$(3-\sqrt{5})a$,$AH^2=(6-2\sqrt{5})a^2$.
∴$AB\cdot HB=2a\times(3-\sqrt{5})a=(6-2\sqrt{5})a^2$.
∴$AH^2=AB\cdot HB$,即$\frac{AH}{AB}=\frac{HB}{AH}$.
∴H是线段AB的黄金分割点.
10. 阅读下面的材料,并解答问题.
小明参加了一次折纸活动,折叠步骤如下:
第一步:在一张宽为2的矩形纸片的一端,利用如图①所示的方法折叠出一个正方形.
第二步:如图②,把纸片展平,将图①中的正方形折成两个相等的矩形.
第三步:把纸片展平,折出图②中内侧矩形的对角线AB,并将AB折到如图③所示的AD处.
第四步:展平纸片,按照所得的点D折出如图④所示的矩形BCDE.
已知矩形BCDE为黄金矩形,你能给出证明吗(注:当矩形的宽与长的比为$\frac{\sqrt{5}-1}{2}$时,称这个矩形为黄金矩形)?
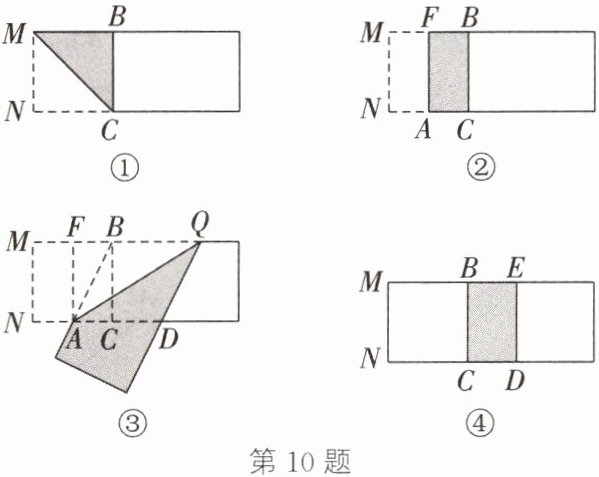
小明参加了一次折纸活动,折叠步骤如下:
第一步:在一张宽为2的矩形纸片的一端,利用如图①所示的方法折叠出一个正方形.
第二步:如图②,把纸片展平,将图①中的正方形折成两个相等的矩形.
第三步:把纸片展平,折出图②中内侧矩形的对角线AB,并将AB折到如图③所示的AD处.
第四步:展平纸片,按照所得的点D折出如图④所示的矩形BCDE.
已知矩形BCDE为黄金矩形,你能给出证明吗(注:当矩形的宽与长的比为$\frac{\sqrt{5}-1}{2}$时,称这个矩形为黄金矩形)?

答案:
在题图③中,由题意可知,$AC=\frac{1}{2}NC=\frac{1}{2}MN=1$.在Rt△ABC中,
∵BC=2,AC=1,
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{5}$.
∵AD=AB=$\sqrt{5}$,
∴$CD=AD-AC=\sqrt{5}-1$.
∴$\frac{CD}{BC}=\frac{\sqrt{5}-1}{2}$.
∴矩形BCDE为黄金矩形
∵BC=2,AC=1,
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{5}$.
∵AD=AB=$\sqrt{5}$,
∴$CD=AD-AC=\sqrt{5}-1$.
∴$\frac{CD}{BC}=\frac{\sqrt{5}-1}{2}$.
∴矩形BCDE为黄金矩形
查看更多完整答案,请扫码查看


