第66页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 方位角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的角(一般指锐角).如图①,图中的角表示
北
偏东
60°.
答案:
北 东
2. 仰角、俯角:如图②,在进行测量时,从下往上看,视线与水平线的夹角($\angle \alpha$)叫做
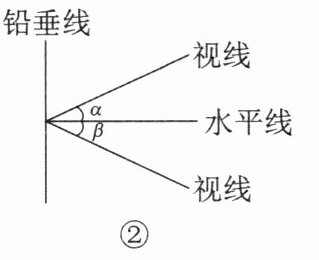
仰角
;从上往下看,视线与水平线的夹角($\angle \beta$)叫做俯角
.
答案:
仰角 俯角
1. 如图,小明从A地沿北偏西60°方向走100 m到达B地,再从B地向正南方向走200 m到达C地,此时小明与A地的距离为 (
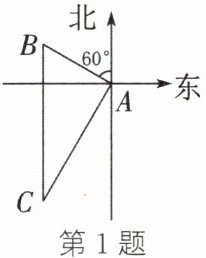
A.$50\sqrt{3}\ \text{m}$
B.100 m
C.150 m
D.$100\sqrt{3}\ \text{m}$
D
)
A.$50\sqrt{3}\ \text{m}$
B.100 m
C.150 m
D.$100\sqrt{3}\ \text{m}$
答案:
D
2. (2024·长春)2024年5月29日16时12分,“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射.如图,当火箭上升到点A处时,位于海平面R处的雷达测得点R到点A的距离为a千米,仰角为$\theta$,则此时火箭距海平面的高度AL为 (
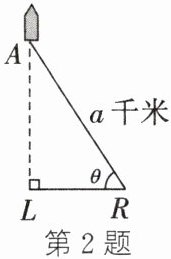
A.$a\sin\theta$千米
B.$\frac{a}{\sin\theta}$千米
C.$a\cos\theta$千米
D.$\frac{a}{\cos\theta}$千米
A
)
A.$a\sin\theta$千米
B.$\frac{a}{\sin\theta}$千米
C.$a\cos\theta$千米
D.$\frac{a}{\cos\theta}$千米
答案:
A
3. (2024·杭州钱塘段考)如图,为确定某隧道AB的长度,测量人员在离地面2700米高度的飞机上(点C处),测得正前方点A处的俯角为60°,BC的坡比为$1:\sqrt{3}$,则隧道AB的长为
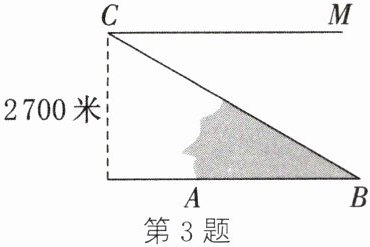
$1800\sqrt{3}$
米(结果保留根号).
答案:
$1800\sqrt{3}$
4. 某市对A地和B地之间的一处垃圾填埋场进行改造,把原来A地去往B地需要绕行到C地的路线改造成可以直线通行的公路AB.如图,经勘测,C地位于A地北偏东30°方向,位于B地北偏西53°方向,AC= 6千米,则改造后公路AB的长约为
9.9
千米(结果精确到0.1千米,参考数据:$\sin37°\approx0.60$,$\cos37°\approx0.80$,$\tan37°\approx0.75$,$\sqrt{3}\approx1.73$).
答案:
9.9
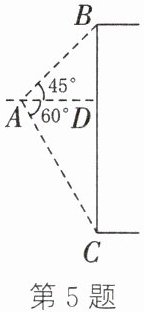
5. (2024·杭州余杭期中)“科技改变生活”,小王是一名摄影爱好者,新入手一台无人机用于航拍.如图,在一次航拍时,数据显示,从无人机A看建筑物顶部B的仰角为45°,看底部C的俯角为60°,无人机A到该建筑物BC的水平距离AD为10米,求该建筑物BC的高度(结果精确到0.1米,参考数据:$\sqrt{2}\approx1.41$,$\sqrt{3}\approx1.73$).

答案:
由题意知,$\angle BAD = 45^{\circ}$,$\angle CAD = 60^{\circ}$,$AD\perp BC$。因为$AD\perp BC$,所以$\angle BDA = \angle ADC = 90^{\circ}$,所以$\angle BAD = \angle ABD = 45^{\circ}$,所以$BD = AD = 10$米。在$Rt\triangle ACD$中,$CD = AD\cdot\tan\angle CAD = AD\cdot\tan60^{\circ}=10\sqrt{3}$米。所以$BC = BD + CD = 10 + 10\sqrt{3}\approx27.3$(米),所以该建筑物$BC$的高度约为$27.3$米。
查看更多完整答案,请扫码查看


