《2025年通城学典课时作业本九年级数学全一册浙教版》

1. 相似多边形:一般地,对应角相等,对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比也叫做相似比.

答案： 相等　成比例　相似比

2. 相似多边形的性质:相似多边形的周长之比等于相似比;相似多边形的面积之比等于相似比的平方.

答案： 相似比　相似比的平方

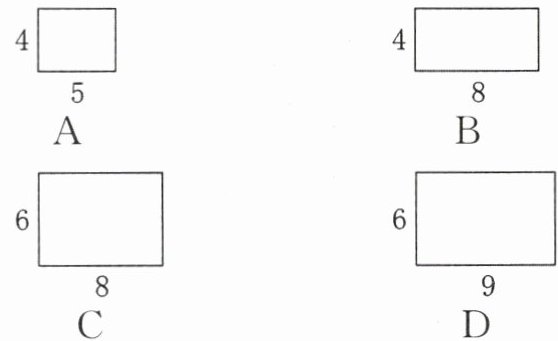
1. (2024·温州鹿城段考)已知矩形的长与宽分别为4和3,下列矩形与它相似的是(C)

答案： C

2. (2024·宁波模拟)矩形相邻的两边长分别为25和x(x＜25),把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则x的值为(B)
A.5
B.5√5
C.5√10
D.10

答案： B

3. (2024·盐城)两个相似多边形的相似比为1:2,则它们的周长之比为1:2.

答案： 1:2

4. 如图,四边形ABCD与四边形A'B'C'D'相似,则BC=25,CD=10,α=80°.

答案： 25　10　80°

5. 在比例尺是1:500的图纸上,测得一块矩形土地的长为5cm,宽为4cm,则这块土地的实际面积为500$m^2.$

答案： 500

6. 如图,在正方形ABCD中,E是对角线BD上一点,且BE= BC,过点E作EF⊥AB,EG⊥BC,垂足分别为F,G,则正方形FBGE与正方形ABCD的相似比为$\frac{\sqrt{2}}{2}$.

答案： $\frac{\sqrt{2}}{2}$

7. 如图,在梯形ABCD中,EF//AB//CD,AB= 9,DC= 4.若梯形DCFE∽梯形EFBA,求EF的长.

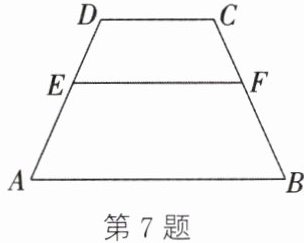
答案：
∵梯形DCFE∽梯形EFBA,
∴$\frac{DC}{EF}$=$\frac{EF}{AB}$，
∴EF²=AB·DC=9×4=36，
∴EF=6

8. (新考向·地域文化)(2024·舟山定海段考)如图①所示为古希腊时期的帕特农神庙,把图①中用虚线表示的矩形画成如图②所示的矩形ABCD,当以矩形ABCD的宽AB为边作正方形ABEF时,惊奇地发现矩形CDFE与矩形ABCD相似,则BE/EC的值为(D)
A.(√5-1)/2
B.3/2
C.(√3+1)/2
D.(√5+1)/2

答案： D