《2025年通城学典课时作业本九年级数学全一册浙教版》

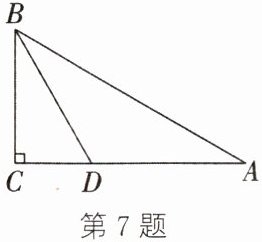
7. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ },\tan A= \frac {\sqrt {3}}{3}$,$\angle ABC$的平分线BD交AC于点D,$CD= \sqrt {3}$,求AB的长.

答案：
∵ 在Rt△ABC中，∠C=90°，$\tan A=\frac{\sqrt{3}}{3}$，
∴ ∠A=30°.
∴ ∠ABC=60°.
∵ BD 是∠ABC 的平分线，
∴ ∠CBD=∠ABD=30°.又
∵ $CD=\sqrt{3}$，
∴ $BC=\frac{CD}{\tan30^\circ}=3$.
∵ 在Rt△ABC中，∠C=90°，∠A=30°，
∴ $AB=\frac{BC}{\sin30^\circ}=6$.
∴ AB的长为6

8. 学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面.如图,彩旗绳与地面形成$25^{\circ }$的角(即$\angle BAC= 25^{\circ }$),彩旗绳固定在地面的位置与图书馆相距32米(即$AC= 32$米),则彩旗绳AB的长度为(D)
A.$32\sin 25^{\circ }$米
B.$32\cos 25^{\circ }$米
C.$\frac {32}{\sin 25^{\circ }}$米
D.$\frac {32}{\cos 25^{\circ }}$米

答案： D

9. 综合实践课上,某航模小组用航拍无人机进行测高实践.如图,无人机从地面CD的中点A处竖直上升30米到达点B处,测得一号楼顶部点E的俯角为$45^{\circ }$,二号楼顶部点F的俯角为$30^{\circ }$.若一号楼的高度CE为15米,则二号楼的高度DF为$(30-5\sqrt{3})$米.

答案： $(30-5\sqrt{3})$

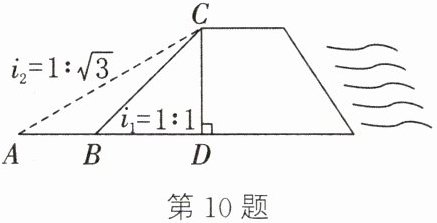
10. 如图所示为某水库大坝的横截面,坝高$CD= 20\ \text{m}$,背水坡BC的坡比$i_{1}= 1:1$.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡比改为$i_{2}= 1:\sqrt {3}$,求背水坡的新起点A与原起点B之间的距离(结果精确到0.1 m,参考数据:$\sqrt {2}\approx 1.414,\sqrt {3}\approx 1.732$).

答案： 在Rt△BCD中，
∵ BC 的坡比$i_1=1:1$，
∴ $\frac{CD}{BD}=1$.
∴ BD=CD=20 m.在Rt△ACD中，
∵ AC 的坡比$i_2=1:\sqrt{3}$，
∴ $\frac{CD}{AD}=\frac{1}{\sqrt{3}}$.
∴ $AD=\sqrt{3}CD=20\sqrt{3}$ m.
∴ $AB=AD-BD=20\sqrt{3}-20\approx14.6(m)$.
∴ 背水坡的新起点A与原起点B之间的距离约为14.6 m