第52页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1.(2024·杭州西湖段考)已知$\frac{a}{4}= \frac{b}{3}$,则$\frac{a-b}{b}$的值是(
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.3
D.$\frac{1}{3}$
D
)A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.3
D.$\frac{1}{3}$
答案:
D
2. 如图,在$\triangle ABC$中,点D在边AB上,点E在边AC上,且$\angle1= \angle2= \angle3$,则与$\triangle ADE$相似的三角形的个数为(
A.4
B.3
C.2
D.1
C
)A.4
B.3
C.2
D.1
答案:
C
3.(2023·安徽)如图,点E在正方形ABCD的对角线AC上,$EF\perp AB$于点F,连结DE并延长,交边BC于点M,交AB的延长线于点G.若$AF= 2$,$FB= 1$,则MG的长为(
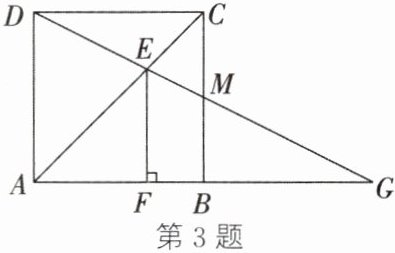
A.$2\sqrt{3}$
B.$\frac{3\sqrt{5}}{2}$
C.$\sqrt{5}+1$
D.$\sqrt{10}$
B
)
A.$2\sqrt{3}$
B.$\frac{3\sqrt{5}}{2}$
C.$\sqrt{5}+1$
D.$\sqrt{10}$
答案:
B 解析:
∵ 四边形ABCD是正方形,AF = 2,FB = 1,
∴ AD = BC = AB = AF + FB = 2 + 1 = 3,AD//CB,AD⊥AB,CB⊥AB.
∵ EF⊥AB,
∴ AD//EF//BC.
∴ $\frac{DE}{EM}=\frac{AF}{FB}=2$,△ADE∽△CME.
∴ $\frac{CM}{AD}=\frac{ME}{DE}=\frac{1}{2}$,则 $CM=\frac{1}{2}AD=\frac{3}{2}$.
∴ $MB=BC - CM=3 - \frac{3}{2}=\frac{3}{2}$.
∵ BC//AD,
∴ △GMB∽△GDA.
∴ $\frac{BG}{AG}=\frac{MB}{DA}=\frac{\frac{3}{2}}{3}=\frac{1}{2}$.
∴ $BG=\frac{1}{2}AG$,即 BG = AB = 3. 在Rt△BGM中,由勾股定理,得 $MG=\sqrt{MB^2+BG^2}=\sqrt{(\frac{3}{2})^2+3^2}=\frac{3\sqrt{5}}{2}$.
∵ 四边形ABCD是正方形,AF = 2,FB = 1,
∴ AD = BC = AB = AF + FB = 2 + 1 = 3,AD//CB,AD⊥AB,CB⊥AB.
∵ EF⊥AB,
∴ AD//EF//BC.
∴ $\frac{DE}{EM}=\frac{AF}{FB}=2$,△ADE∽△CME.
∴ $\frac{CM}{AD}=\frac{ME}{DE}=\frac{1}{2}$,则 $CM=\frac{1}{2}AD=\frac{3}{2}$.
∴ $MB=BC - CM=3 - \frac{3}{2}=\frac{3}{2}$.
∵ BC//AD,
∴ △GMB∽△GDA.
∴ $\frac{BG}{AG}=\frac{MB}{DA}=\frac{\frac{3}{2}}{3}=\frac{1}{2}$.
∴ $BG=\frac{1}{2}AG$,即 BG = AB = 3. 在Rt△BGM中,由勾股定理,得 $MG=\sqrt{MB^2+BG^2}=\sqrt{(\frac{3}{2})^2+3^2}=\frac{3\sqrt{5}}{2}$.
4. 如图,在$\triangle ABC$中,点D,F在边AB上,点E,G在边AC上,$DE// FG// BC$,且$AD:DF:FB= 3:2:1$.若$AG= 15$,则CE的长为______
9
.
答案:
9
5. 如图,$\angle ACB= \angle BDC= 90^\circ$.给出下列条件:①$AB// CD$;②$BC^2= AC\cdot CD$;③$\frac{AC}{BC}= \frac{BD}{CD}$.其中,添加后能使$\triangle ABC\sim\triangle BCD$的是
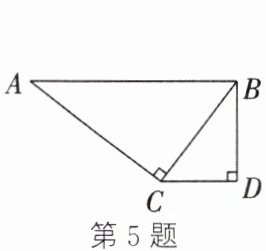
①③
(填序号).
答案:
①③
6.(2023·山西)如图,在四边形ABCD中,$\angle BCD= 90^\circ$,对角线AC,BD相交于点O.如果$AB= AC= 5$,$BC= 6$,$\angle ADB= 2\angle CBD$,那么AD的长为______
$\frac{\sqrt{97}}{3}$
.
答案:
$\frac{\sqrt{97}}{3}$ 解析:如图,过点A作AH⊥BC于点H,延长AD,BC交于点E,则∠AHC = ∠AHB = 90°.
∵ AB = AC = 5,BC = 6,
∴ $BH=HC=\frac{1}{2}BC = 3$.
∴ $AH=\sqrt{AC^2 - CH^2}=4$.
∵ ∠ADB = ∠CBD + ∠CED,∠ADB = 2∠CBD,
∴ ∠CBD = ∠CED.
∴ DB = DE.
∵ ∠BCD = 90°,
∴ DC⊥BE.
∴ CE = BC = 6.
∴ EH = CE + CH = 9.
∵ DC⊥BE,AH⊥BC,
∴ CD//AH.
∴ △ECD∽△EHA.
∴ $\frac{CD}{HA}=\frac{CE}{HE}$,即 $\frac{CD}{4}=\frac{6}{9}$.
∴ $CD=\frac{8}{3}$.
∴ $DE=\sqrt{CE^2+CD^2}=\sqrt{6^2+(\frac{8}{3})^2}=\frac{2\sqrt{97}}{3}$.
∵ CD//AH,
∴ $\frac{DE}{AD}=\frac{CE}{HC}$,即 $\frac{\frac{2\sqrt{97}}{3}}{AD}=\frac{6}{3}$,解得 $AD=\frac{\sqrt{97}}{3}$.
∵ AB = AC = 5,BC = 6,
∴ $BH=HC=\frac{1}{2}BC = 3$.
∴ $AH=\sqrt{AC^2 - CH^2}=4$.
∵ ∠ADB = ∠CBD + ∠CED,∠ADB = 2∠CBD,
∴ ∠CBD = ∠CED.
∴ DB = DE.
∵ ∠BCD = 90°,
∴ DC⊥BE.
∴ CE = BC = 6.
∴ EH = CE + CH = 9.
∵ DC⊥BE,AH⊥BC,
∴ CD//AH.
∴ △ECD∽△EHA.
∴ $\frac{CD}{HA}=\frac{CE}{HE}$,即 $\frac{CD}{4}=\frac{6}{9}$.
∴ $CD=\frac{8}{3}$.
∴ $DE=\sqrt{CE^2+CD^2}=\sqrt{6^2+(\frac{8}{3})^2}=\frac{2\sqrt{97}}{3}$.
∵ CD//AH,
∴ $\frac{DE}{AD}=\frac{CE}{HC}$,即 $\frac{\frac{2\sqrt{97}}{3}}{AD}=\frac{6}{3}$,解得 $AD=\frac{\sqrt{97}}{3}$.
7. 如图,在由小正方形组成的网格中,每个小正方形的边长均为1,$\triangle ABC与\triangle ADE$的顶点都在格点上.
(1)求证:$\triangle ADE\sim\triangle ABC$;
(2)求$\angle1+\angle2$的度数.
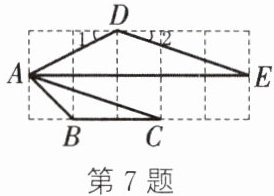
(1)求证:$\triangle ADE\sim\triangle ABC$;
(2)求$\angle1+\angle2$的度数.

答案:
(1)由勾股定理,得 $AD=\sqrt{2^2+1^2}=\sqrt{5}$,$DE=\sqrt{3^2+1^2}=\sqrt{10}$,$AB=\sqrt{1^2+1^2}=\sqrt{2}$,$AC=\sqrt{1^2+3^2}=\sqrt{10}$. 又
∵ AE = 5,BC = 2,
∴ $\frac{AD}{AB}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{10}}{2}$,$\frac{DE}{BC}=\frac{\sqrt{10}}{2}$,$\frac{AE}{AC}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}$.
∴ $\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$.
∴ △ADE∽△ABC.
(2)由
(1),得△ADE∽△ABC,
∴ ∠ADE = ∠ABC = 90° + 45° = 135°.
∴ ∠1 + ∠2 = 180° - ∠ADE = 45°.
(1)由勾股定理,得 $AD=\sqrt{2^2+1^2}=\sqrt{5}$,$DE=\sqrt{3^2+1^2}=\sqrt{10}$,$AB=\sqrt{1^2+1^2}=\sqrt{2}$,$AC=\sqrt{1^2+3^2}=\sqrt{10}$. 又
∵ AE = 5,BC = 2,
∴ $\frac{AD}{AB}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{10}}{2}$,$\frac{DE}{BC}=\frac{\sqrt{10}}{2}$,$\frac{AE}{AC}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}$.
∴ $\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$.
∴ △ADE∽△ABC.
(2)由
(1),得△ADE∽△ABC,
∴ ∠ADE = ∠ABC = 90° + 45° = 135°.
∴ ∠1 + ∠2 = 180° - ∠ADE = 45°.
查看更多完整答案,请扫码查看


