第23页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
7. (新情境·日常生活)(2024·武汉)经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆汽车向右转的概率是(
A.$\frac{1}{9}$
B.$\frac{1}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
D
)A.$\frac{1}{9}$
B.$\frac{1}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$
答案:
D
8. 动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5.若设刚出生的这种动物共有$a$只,则20年后存活的约有
$0.8a$
只,现年20岁的这种动物活到25岁的概率是$\frac{5}{8}$
.
答案:
$0.8a$ $\frac{5}{8}$
9. (2024·扬州)2024年“五一”假期,扬州各旅游景区持续火热.小明和小亮准备到东关街、瘦西湖、运河三湾风景区、个园、何园(分别记做A,B,C,D,E)参加公益讲解活动.
(1)若小明在这5个景区中随机选择1个景区,则选中东关街的概率是______;
(2)小明和小亮在C,D,E三个景区中,各自随机选择1个景区,请用画树状图或列表的方法,求小明和小亮选到相同景区的概率.
(1)若小明在这5个景区中随机选择1个景区,则选中东关街的概率是______;
(2)小明和小亮在C,D,E三个景区中,各自随机选择1个景区,请用画树状图或列表的方法,求小明和小亮选到相同景区的概率.
答案:
(1)$\frac{1}{5}$;(2)列表如下:
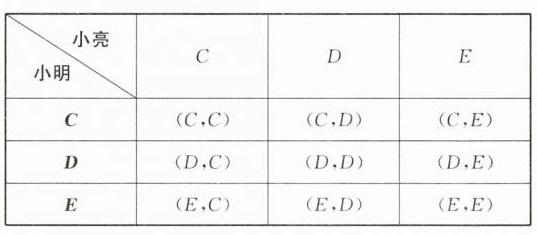
由表格可知,共有 9 种等可能的结果,其中小明和小亮选到相同景区的结果有 3 种,
∴小明和小亮选到相同景区的概率为$\frac{3}{9}=\frac{1}{3}$
(1)$\frac{1}{5}$;(2)列表如下:

由表格可知,共有 9 种等可能的结果,其中小明和小亮选到相同景区的结果有 3 种,
∴小明和小亮选到相同景区的概率为$\frac{3}{9}=\frac{1}{3}$
10. 某商场开展“真情回报社会”的幸运抽奖活动,共设五个奖金等级,最高奖金每份1万元,平均奖金180元,下面是奖金的分配表:
|奖金等级|奖金额(元)|中奖人数|
|一等奖|10000|3|
|二等奖|5000|8|
|三等奖|1000|89|
|四等奖|50|300|
|五等奖|10|600|
一名顾客抽到一张奖券,奖金额为10元,她调查了周围不少正在兑奖的其他顾客,很少有超过50元的.她去找商场的领导理论,领导解释说这不存在什么欺骗,平均奖金确实是180元.你认为商场所说的平均奖金是否欺骗了顾客?此种说法是否能够很好地反映中奖的一般金额?用统计与概率的有关知识进行分析说明.
|奖金等级|奖金额(元)|中奖人数|
|一等奖|10000|3|
|二等奖|5000|8|
|三等奖|1000|89|
|四等奖|50|300|
|五等奖|10|600|
一名顾客抽到一张奖券,奖金额为10元,她调查了周围不少正在兑奖的其他顾客,很少有超过50元的.她去找商场的领导理论,领导解释说这不存在什么欺骗,平均奖金确实是180元.你认为商场所说的平均奖金是否欺骗了顾客?此种说法是否能够很好地反映中奖的一般金额?用统计与概率的有关知识进行分析说明.
答案:
根据题意,得这次抽奖的平均奖金为$\frac{10000×3+5000×8+1000×89+50×300+10×600}{3+8+89+300+600}=180$(元).
∴商场所说的平均奖金没有欺骗顾客
∵P(中奖金额不超过 50 元)=$\frac{300+600}{3+8+89+300+600}=0.9$,P(中奖金额超过 50 元)=1 - 0.9=0.1,中奖金额的众数为 10 元,中位数为 10 元,
∴此种说法不能够很好地反映中奖的一般金额
∴商场所说的平均奖金没有欺骗顾客
∵P(中奖金额不超过 50 元)=$\frac{300+600}{3+8+89+300+600}=0.9$,P(中奖金额超过 50 元)=1 - 0.9=0.1,中奖金额的众数为 10 元,中位数为 10 元,
∴此种说法不能够很好地反映中奖的一般金额
查看更多完整答案,请扫码查看


