第16页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 如图,$\text{Rt}\triangle OAB的顶点A(-2,4)在抛物线y= ax^{2}$上,点$D在y$轴上,$\text{Rt}\triangle OCD \cong \text{Rt}\triangle OAB$,边$CD与该抛物线交于点P$,则点$P$的坐标为(
A.$(\sqrt{2},\sqrt{2})$
B.$(2,2)$
C.$(\sqrt{2},2)$
D.$(2,\sqrt{2})$
C
)A.$(\sqrt{2},\sqrt{2})$
B.$(2,2)$
C.$(\sqrt{2},2)$
D.$(2,\sqrt{2})$
答案:
C
2. (2024·资阳改编)在平面直角坐标系中,抛物线$y= -\dfrac{1}{2}x^{2}+bx+c与x轴交于A$,$B$两点,与$y轴的正半轴交于点C$,且点$B的坐标为(4,0)$,$BC= 4\sqrt{2}$.
(1)求抛物线对应的函数表达式.
(2)如图,$P$是抛物线在第一象限内的一点,连结$PB$,$PC$,过点$P作PD \perp x轴于点D$,交$BC于点K$.记$\triangle PBC$,$\triangle BDK的面积分别为S_{1}$,$S_{2}$,求$S_{1}-S_{2}$的最大值.
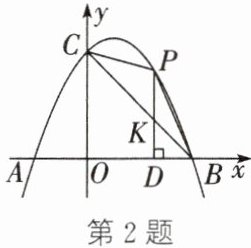
(1)求抛物线对应的函数表达式.
(2)如图,$P$是抛物线在第一象限内的一点,连结$PB$,$PC$,过点$P作PD \perp x轴于点D$,交$BC于点K$.记$\triangle PBC$,$\triangle BDK的面积分别为S_{1}$,$S_{2}$,求$S_{1}-S_{2}$的最大值.

答案:
(1)
∵B(4,0),
∴OB=4.
∵∠BOC=90°,BC=4$\sqrt{2}$,
∴OC= $\sqrt{BC²−OB²}$=4.又
∵点C在y轴的正半轴上,
∴C(0,4).把B(4,0),C(0,4)代入y= −$\frac{1}{2}$x²+bx+c,得$\begin{cases}-\frac{1}{2}×4² + 4b + c = 0 \\ c = 4\end{cases}$,解得$\begin{cases}b = 1 \\ c = 4\end{cases}$.
∴抛物线对应的函数表达式为y=−$\frac{1}{2}$x²+x+4.
(2)由B(4,0),C(0,4),易得直线BC对应的函数表达式为y=−x+4.设P(m,−$\frac{1}{2}$m²+m+4),0<m<4,则K(m,−m+4),D(m,0).
∴PK=−$\frac{1}{2}$m²+m+4−(−m+4)=−$\frac{1}{2}$m²+2m,DK=−m+4,DB=4−m.
∴S₁=$\frac{1}{2}$PK·OB=−m²+4m,S₂=$\frac{1}{2}$DK·DB=$\frac{1}{2}$(−m+4)(4−m)=$\frac{1}{2}$(4−m)².
∴S₁−S₂=−m²+4m−$\frac{1}{2}$(4−m)²=−$\frac{3}{2}$m²+8m−8=−$\frac{3}{2}$(m−$\frac{8}{3}$)²+$\frac{8}{3}$.
∵−$\frac{3}{2}$<0,
∴当m=$\frac{8}{3}$时,S₁−S₂取得最大值,为$\frac{8}{3}$.
(1)
∵B(4,0),
∴OB=4.
∵∠BOC=90°,BC=4$\sqrt{2}$,
∴OC= $\sqrt{BC²−OB²}$=4.又
∵点C在y轴的正半轴上,
∴C(0,4).把B(4,0),C(0,4)代入y= −$\frac{1}{2}$x²+bx+c,得$\begin{cases}-\frac{1}{2}×4² + 4b + c = 0 \\ c = 4\end{cases}$,解得$\begin{cases}b = 1 \\ c = 4\end{cases}$.
∴抛物线对应的函数表达式为y=−$\frac{1}{2}$x²+x+4.
(2)由B(4,0),C(0,4),易得直线BC对应的函数表达式为y=−x+4.设P(m,−$\frac{1}{2}$m²+m+4),0<m<4,则K(m,−m+4),D(m,0).
∴PK=−$\frac{1}{2}$m²+m+4−(−m+4)=−$\frac{1}{2}$m²+2m,DK=−m+4,DB=4−m.
∴S₁=$\frac{1}{2}$PK·OB=−m²+4m,S₂=$\frac{1}{2}$DK·DB=$\frac{1}{2}$(−m+4)(4−m)=$\frac{1}{2}$(4−m)².
∴S₁−S₂=−m²+4m−$\frac{1}{2}$(4−m)²=−$\frac{3}{2}$m²+8m−8=−$\frac{3}{2}$(m−$\frac{8}{3}$)²+$\frac{8}{3}$.
∵−$\frac{3}{2}$<0,
∴当m=$\frac{8}{3}$时,S₁−S₂取得最大值,为$\frac{8}{3}$.
3. 如图,四边形$OABC$是边长为1的正方形,$OC与x轴正半轴的夹角为15^{\circ}$,点$B在抛物线y= ax^{2}(a<0)$上,则$a$的值为(
A.$-\dfrac{2}{3}$
B.$-\dfrac{\sqrt{2}}{3}$
C.$-2$
D.$-\dfrac{1}{2}$
B
)A.$-\dfrac{2}{3}$
B.$-\dfrac{\sqrt{2}}{3}$
C.$-2$
D.$-\dfrac{1}{2}$
答案:
B
4. 如图,$P是抛物线y= x^{2}-x-4$在第四象限的一点,过点$P分别向x轴和y$轴作垂线,垂足分别为$A$,$B$,则四边形$OAPB$周长的最大值为(
A.10
B.8
C.7.5
D.$5\sqrt{3}$
A
)A.10
B.8
C.7.5
D.$5\sqrt{3}$
答案:
A
5. 如图,菱形$OABC的顶点O$,$A$,$C在抛物线y= \dfrac{1}{3}x^{2}$上,其中$O$为坐标原点,对角线$OB在y$轴上,且$OB= 2$,则菱形$OABC$的面积为______
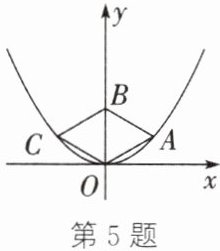
2$\sqrt{3}$
.
答案:
2$\sqrt{3}$
6. 如图,在平面直角坐标系中,抛物线$y= \dfrac{1}{3}x^{2}-\dfrac{1}{3}x-4交x轴于A$,$B$两点(点$A在点B$的左侧),交$y轴于点C$.$P为线段BC$下方抛物线上的任意一点,一动点$G从点P$出发,沿适当路径以每秒1个单位的速度运动到$y轴上的点M$,再沿适当路径以每秒1个单位的速度运动到$x轴上的点N$,最后沿$x轴以每秒\sqrt{2}个单位的速度运动到点B$.当四边形$ACPB$的面积最大时,求运动时间$t$的最小值.
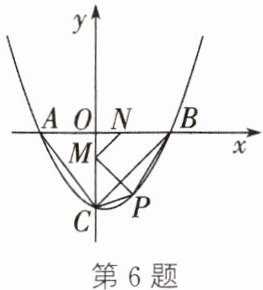

答案:
y=$\frac{1}{3}$x²−$\frac{1}{3}$x−4,令x=0,则y=−4,令y=0,则x=−3或x=4,故点A,B,C的坐标分别为(−3,0),(4,0),(0,−4).
∴直线BC对应的函数表达式为y=x−4.
∵S四边形ACP B=S△ABC+S△PBC,S△ABC为定值,
∴只要S△PBC取得最大值,四边形ACPB的面积即为最大.如图,过点P作PS⊥x轴交BC于点S.设P(m,$\frac{1}{3}$m²−$\frac{1}{3}$m−4),0<m<4,则S(m,m−4),S△PBC=$\frac{1}{2}$×OB·PS=$\frac{1}{2}$×4×(m−4−$\frac{1}{3}$m²+$\frac{1}{3}$m+4)=−$\frac{2}{3}$m²+$\frac{8}{3}$m=−$\frac{2}{3}$(m−2)²+$\frac{8}{3}$.
∵ −$\frac{2}{3}$<0,
∴当m=2时,S△PBC有最大值,即四边形ACPB的面积有最大值.
∴P(2,−$\frac{10}{3}$).作点P关于y轴的对称点P',可得P’(−2,−$\frac{10}{3}$),过点B作BK⊥BC交y轴于点K,作P'H⊥BK于点H,交y轴于点M,交x轴于点N,则此时运动时间t的值最小.易得△BNH为等腰直角三角形,
∴t=PM+MN+$\frac{\sqrt{2}}{2}$BN=P'M+MN+HN=P'H.
∵∠KBO=45°、∠KOB=90°,
∴∠OKB=45°.
∴KO=OB.
∵B(4,0),
∴K(0,4).
∴易得直线BK对应的函数表达式为y=−x+4①.
∵P'H⊥BK,BC⊥BK,
∴P'H//BC.
∴易得直线P'H对应的函数表达式为y=x−$\frac{4}{3}$②.联立①②,解得$\begin{cases}x = \frac{8}{3} \\ y = \frac{4}{3}\end{cases}$.故H($\frac{8}{3}$,$\frac{4}{3}$).
∴t=P'H= $\sqrt{(-2 - \frac{8}{3})² + (-\frac{10}{3} - \frac{4}{3})²}$ = $\frac{14\sqrt{2}}{3}$.
∴运动时间t的最小值为$\frac{14\sqrt{2}}{3}$.

y=$\frac{1}{3}$x²−$\frac{1}{3}$x−4,令x=0,则y=−4,令y=0,则x=−3或x=4,故点A,B,C的坐标分别为(−3,0),(4,0),(0,−4).
∴直线BC对应的函数表达式为y=x−4.
∵S四边形ACP B=S△ABC+S△PBC,S△ABC为定值,
∴只要S△PBC取得最大值,四边形ACPB的面积即为最大.如图,过点P作PS⊥x轴交BC于点S.设P(m,$\frac{1}{3}$m²−$\frac{1}{3}$m−4),0<m<4,则S(m,m−4),S△PBC=$\frac{1}{2}$×OB·PS=$\frac{1}{2}$×4×(m−4−$\frac{1}{3}$m²+$\frac{1}{3}$m+4)=−$\frac{2}{3}$m²+$\frac{8}{3}$m=−$\frac{2}{3}$(m−2)²+$\frac{8}{3}$.
∵ −$\frac{2}{3}$<0,
∴当m=2时,S△PBC有最大值,即四边形ACPB的面积有最大值.
∴P(2,−$\frac{10}{3}$).作点P关于y轴的对称点P',可得P’(−2,−$\frac{10}{3}$),过点B作BK⊥BC交y轴于点K,作P'H⊥BK于点H,交y轴于点M,交x轴于点N,则此时运动时间t的值最小.易得△BNH为等腰直角三角形,
∴t=PM+MN+$\frac{\sqrt{2}}{2}$BN=P'M+MN+HN=P'H.
∵∠KBO=45°、∠KOB=90°,
∴∠OKB=45°.
∴KO=OB.
∵B(4,0),
∴K(0,4).
∴易得直线BK对应的函数表达式为y=−x+4①.
∵P'H⊥BK,BC⊥BK,
∴P'H//BC.
∴易得直线P'H对应的函数表达式为y=x−$\frac{4}{3}$②.联立①②,解得$\begin{cases}x = \frac{8}{3} \\ y = \frac{4}{3}\end{cases}$.故H($\frac{8}{3}$,$\frac{4}{3}$).
∴t=P'H= $\sqrt{(-2 - \frac{8}{3})² + (-\frac{10}{3} - \frac{4}{3})²}$ = $\frac{14\sqrt{2}}{3}$.
∴运动时间t的最小值为$\frac{14\sqrt{2}}{3}$.

查看更多完整答案,请扫码查看


