第46页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 相似三角形
(1)定义:一般地,对应角
(2)符号表示:相似用符号“
(1)定义:一般地,对应角
相等
,对应边成比例
的两个三角形,叫做相似三角形. 相似三角形对应边的比叫做相似比
.(2)符号表示:相似用符号“
∽
”表示,读做“相似于
”.
答案:
(1)相等 成比例 相似比 (2)∽ 相似于
2. 相似三角形的性质:相似三角形的对应角
相等
,对应边成比例
.
答案:
相等 成比例
1. (2024·温州鹿城段考)如图,$\triangle ABC\backsim\triangle DEF$,则$DF$的长是(
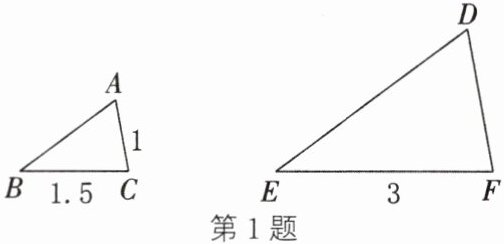
A.$\sqrt{2}$
B.$\sqrt{3}$
C.2
D.3
C
)
A.$\sqrt{2}$
B.$\sqrt{3}$
C.2
D.3
答案:
C
2. (2024·温州鹿城段考)如图,$\triangle ABC\backsim\triangle AED$,$DE与BC$不平行. 若$\angle A= 50^\circ$,$\angle AED= 55^\circ$,则$\angle ACB$的度数为(
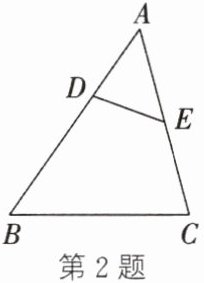
A.$55^\circ$
B.$65^\circ$
C.$75^\circ$
D.$85^\circ$
C
)
A.$55^\circ$
B.$65^\circ$
C.$75^\circ$
D.$85^\circ$
答案:
C
3. (2024·杭州余杭期中)已知$\triangle ABC\backsim\triangle DEF$. 若$\angle A= 30^\circ$,$\angle E= 70^\circ$,则$\angle F$的度数为(
A.$30^\circ$
B.$70^\circ$
C.$80^\circ$
D.$120^\circ$
C
)A.$30^\circ$
B.$70^\circ$
C.$80^\circ$
D.$120^\circ$
答案:
C
4. 如图,$\triangle ABO\backsim\triangle CDO$. 若$BO= 6$,$DO= 3$,$CD= 2$,则$AB$的长是(
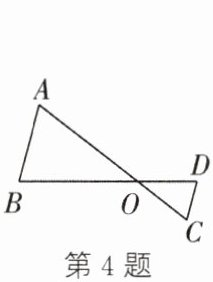
A.2
B.3
C.4
D.5
C
) 
A.2
B.3
C.4
D.5
答案:
C
5. 如图,$\triangle ADE\backsim\triangle ABC$,$AD= 3$,$AE= 4$,$BE= 5$,则$AC$的长为______
12
.
答案:
12
6. 如图,$\triangle ABC\backsim\triangle ADE$,点$D在线段BE$上,则图中与$\angle BAD$相等的角为
∠CAE,∠CBD
.
答案:
∠CAE,∠CBD
7. 如图,$\triangle ABC\backsim\triangle DAC$,$DA= 2$,$CA= 4$,$BC= 6$,$\angle B= 36^\circ$,$\angle D= 117^\circ$. 求:
(1)$AB$,$CD$的长;
(2)$\angle BAD$的度数.
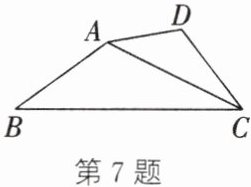
(1)$AB$,$CD$的长;
(2)$\angle BAD$的度数.

答案:
(1)
∵△ABC∽△DAC,
∴$\frac{AB}{DA}=\frac{BC}{AC}=\frac{CA}{CD}$.
∵DA=2,CA=4,BC=6,
∴$\frac{AB}{2}=\frac{6}{4}=\frac{4}{CD}$,
∴AB=3,CD=$\frac{8}{3}$
(2)
∵△ABC∽△DAC,∠B=36°,∠D=117°,
∴∠BAC=∠D=117°,∠DAC=∠B=36°.
∴∠BAD=∠BAC+∠DAC=117°+36°=153°
∵△ABC∽△DAC,
∴$\frac{AB}{DA}=\frac{BC}{AC}=\frac{CA}{CD}$.
∵DA=2,CA=4,BC=6,
∴$\frac{AB}{2}=\frac{6}{4}=\frac{4}{CD}$,
∴AB=3,CD=$\frac{8}{3}$
(2)
∵△ABC∽△DAC,∠B=36°,∠D=117°,
∴∠BAC=∠D=117°,∠DAC=∠B=36°.
∴∠BAD=∠BAC+∠DAC=117°+36°=153°
8. 如图,$D是AB$的中点,$\triangle ABC\backsim\triangle ACD$,且$AD= 2$,$\angle ADC= 65^\circ$.
(1)写出$\triangle ABC与\triangle ACD$的对应边成比例的比例式;
(2)求$AC的长及\angle ACB$的度数.
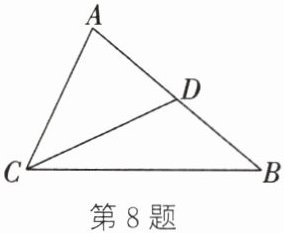
(1)写出$\triangle ABC与\triangle ACD$的对应边成比例的比例式;
(2)求$AC的长及\angle ACB$的度数.

答案:
(1)
∵△ABC∽△ACD,
∴$\frac{AC}{AD}=\frac{AB}{AC}=\frac{BC}{CD}$ (2)由(1),知$\frac{AC}{AD}=\frac{AB}{AC}$.又
∵AD=2,D是AB的中点,
∴AB=2AD=4.
∴$\frac{AC}{2}=\frac{4}{AC}$.
∴AC=2$\sqrt{2}$.
∵△ABC∽△ACD,∠ADC=65°,
∴∠ACB=∠ADC=65°
∵△ABC∽△ACD,
∴$\frac{AC}{AD}=\frac{AB}{AC}=\frac{BC}{CD}$ (2)由(1),知$\frac{AC}{AD}=\frac{AB}{AC}$.又
∵AD=2,D是AB的中点,
∴AB=2AD=4.
∴$\frac{AC}{2}=\frac{4}{AC}$.
∴AC=2$\sqrt{2}$.
∵△ABC∽△ACD,∠ADC=65°,
∴∠ACB=∠ADC=65°
查看更多完整答案,请扫码查看


