第64页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
定义:在直角三角形中,由已知的一些边、角,求出另一些
边、角
的过程,叫做解直角三角形.
答案:
边、角
1. 如图,在△ABC中,∠C= 90°,设∠A,∠B,∠C所对的边分别为a,b,c,则下列四个等式中,一定成立的是 (
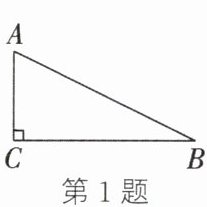
A.c= b·sin B
B.a= c·cos B
C.a= b·tan B
D.b= c·tan B
B
)
A.c= b·sin B
B.a= c·cos B
C.a= b·tan B
D.b= c·tan B
答案:
B
2. (2023·南充)如图,小兵从点A处出发向正东方向走x米到达点B处,再向正北方向走到点C处.若∠BAC= α,则A,C两点相距 (
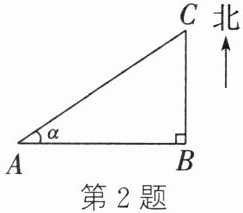
A.$\frac{x}{\sin\alpha}$米
B.$\frac{x}{\cos\alpha}$米
C.$x\sin\alpha$米
D.$x\cos\alpha$米
B
)
A.$\frac{x}{\sin\alpha}$米
B.$\frac{x}{\cos\alpha}$米
C.$x\sin\alpha$米
D.$x\cos\alpha$米
答案:
B
3. 如图所示的图形源于我国数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则cosα的值为 (
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
D
)A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
答案:
D
4. 如图,在Rt△ABC中,∠ACB= 90°,CD是斜边AB上的高线,AD= 8,$\tan\angle BCD= \frac{1}{2}$,则BD的长为
2
.
答案:
2
5. 如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光恰好不能射入窗户,则AB的长是
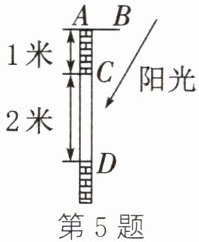
$\sqrt{3}$
米(假设夏至的正午时刻阳光与地面所夹的锐角为60°).
答案:
$\sqrt{3}$
6. 在Rt△ACB中,∠C= 90°,根据下面的条件解直角三角形:
(1)$a= \sqrt{3}-1$,$b= 3-\sqrt{3}$;
(2)∠A= 60°,$c= 2+\sqrt{3}$.
(1)$a= \sqrt{3}-1$,$b= 3-\sqrt{3}$;
(2)∠A= 60°,$c= 2+\sqrt{3}$.
答案:
(1)由$\tan B=\frac{b}{a}=\frac{3-\sqrt{3}}{\sqrt{3}-1}=\sqrt{3}$,得$\angle B=60^{\circ}$.$\therefore\angle A=90^{\circ}-\angle B=30^{\circ}$.由$\sin A=\frac{a}{c}$,得$c=\frac{a}{\sin A}=\frac{\sqrt{3}-1}{\sin30^{\circ}}=2\sqrt{3}-2$ (2)$\angle B=90^{\circ}-\angle A=90^{\circ}-60^{\circ}=30^{\circ}$.由$\sin A=\frac{a}{c}$,得$a=c\sin A=(2+\sqrt{3})×\frac{\sqrt{3}}{2}=\sqrt{3}+\frac{3}{2}$.由$\cos A=\frac{b}{c}$,得$b=c\cos A=(2+\sqrt{3})×\frac{1}{2}=\frac{2+\sqrt{3}}{2}$
查看更多完整答案,请扫码查看


