第48页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
相似三角形的判定定理 2:两边
对应成比例
,且夹角相等
的两个三角形相似.
答案:
对应成比例 相等
1. 如图,在△ABC 中,AB= AC= 6,∠B= 75°,则下列四个三角形中,与△ABC 相似的是(
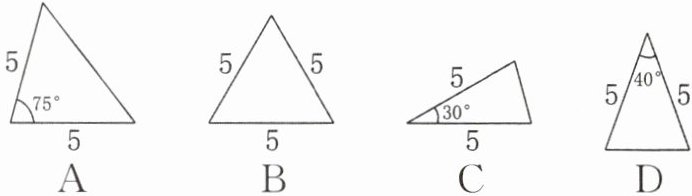
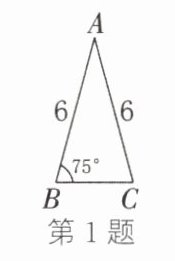
C
)

答案:
C
2. 如图,四边形 ABCD 的对角线 AC,BD 相交于点 O,且将这个四边形分成①②③④四个三角形.若 OA∶OC= OB∶OD,则下列结论一定正确的是(
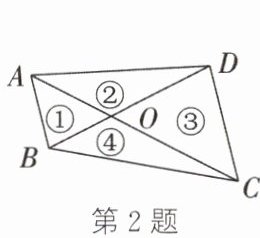
A.①②相似
B.①③相似
C.①④相似
D.②④相似
B
)
A.①②相似
B.①③相似
C.①④相似
D.②④相似
答案:
B
3. (易错题)(教材 P136 作业题第 1 题变式)如图,能使△ABC∽△ADE 成立的条件是(
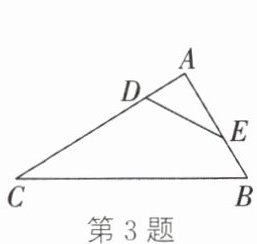
A.∠A= ∠A
B.∠ADE= ∠AED
C.$\frac{AB}{AD}= \frac{AC}{AE}$
D.$\frac{AB}{AE}= \frac{BC}{ED}$
C
)
A.∠A= ∠A
B.∠ADE= ∠AED
C.$\frac{AB}{AD}= \frac{AC}{AE}$
D.$\frac{AB}{AE}= \frac{BC}{ED}$
答案:
C [易错分析]相似三角形中的“A”字型模型分为平行型与非平行型,切莫混淆.
4. (2024·慈溪段考)如图,正方形 ABCD 的边长为 6,F 为 AB 的中点,点 E 在 AD 上,且 ED= 2AE,在边 CD 上找一点 P,使以 E,D,P 为顶点的三角形与△AEF 相似,则 DP 的长为
6或$\frac{8}{3}$
.
答案:
6或$\frac{8}{3}$
5. (2024·绍兴上虞段考)如图,在△ABC 中,AB= 6 cm,AC= 12 cm,动点 D 从点 A 出发,沿 AB 运动到点 B 停止,动点 E 从点 C 出发,沿 CA 运动到点 A 停止,点 D 的运动速度为 1 cm/s,点 E 的运动速度为 2 cm/s.若 D,E 两点同时出发,则当以 A,D,E 为顶点的三角形与△ABC 相似时,运动时间为
3或4.8
s.
答案:
3或4.8 解析:设运动时间为t s时,以A,D,E为顶点的三角形与△ABC相似,则AD=t cm,CE=2t cm,AE=AC-CE=(12-2t)cm. ① △ADE∽△ABC,则$\frac{AD}{AB}=\frac{AE}{AC}$,即$\frac{t}{6}=\frac{12-2t}{12}$,解得t=3. ② △ADE∽△ACB,则$\frac{AD}{AC}=\frac{AE}{AB}$,即$\frac{t}{12}=\frac{12-2t}{6}$,解得t=4.8.
∴当以A,D,E为顶点的三角形与△ABC相似时,运动时间为3s或4.8s.
∴当以A,D,E为顶点的三角形与△ABC相似时,运动时间为3s或4.8s.
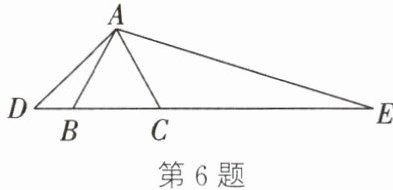
6. 如图,在△ABC 中,AB= AC,D 为 CB 的延长线上一点,E 为 BC 的延长线上一点,且满足$AB^{2}= DB\cdot EC$.求证:△ADB∽△EAC.

答案:
∵AB=AC,
∴∠ABC=∠ACB.
∴易得∠ABD=∠ECA.
∵AB²=DB·EC,
∴$\frac{AB}{EC}=\frac{DB}{AB}$.
∵$\frac{AB}{EC}=\frac{DB}{AC}$.
∴△ADB∽△EAC
∵AB=AC,
∴∠ABC=∠ACB.
∴易得∠ABD=∠ECA.
∵AB²=DB·EC,
∴$\frac{AB}{EC}=\frac{DB}{AB}$.
∵$\frac{AB}{EC}=\frac{DB}{AC}$.
∴△ADB∽△EAC
查看更多完整答案,请扫码查看


