第17页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
7. (2023·鸡西)如图,抛物线$y= ax^{2}+bx+3与x轴交于A(-3,0)$,$B(1,0)$两点,交$y轴于点C$.
(1)求抛物线对应的函数表达式.
(2)抛物线上是否存在一点$P$,使得$S_{\triangle PBC}= \dfrac{1}{2}S_{\triangle ABC}$?若存在,请求出点$P$的坐标;若不存在,请说明理由.
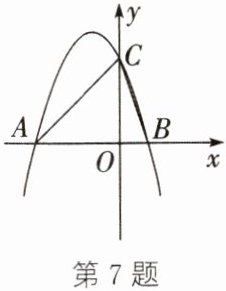
(1)求抛物线对应的函数表达式.
(2)抛物线上是否存在一点$P$,使得$S_{\triangle PBC}= \dfrac{1}{2}S_{\triangle ABC}$?若存在,请求出点$P$的坐标;若不存在,请说明理由.

答案:
(1)把A(−3,0),B(1,0)代入y=ax²+bx+3,得$\begin{cases}9a - 3b + 3 = 0 \\ a + b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1 \\ b = -2\end{cases}$.
∴抛物线对应的函数表达式为y=−x²−2x+3.
(2)存在.
∵A(−3,0),B(1,0),
∴AB=4.在y=−x²−2x+3中,令x=0,则y=3,
∴C(0,3).
∴OC=3.
∴S△ABC=$\frac{1}{2}$AB·OC=$\frac{1}{2}$×4×3=6.
∴S△PBC=$\frac{1}{2}$S△ABC=3.如图,过点P作PE//x轴,交BC于点E,连结BP,CP.设直线BC对应的函数表达式为y=mx+n.将B(1,0),C(0,3)代入,得$\begin{cases}m + n = 0 \\ n = 3\end{cases}$,解得$\begin{cases}m = -3 \\ n = 3\end{cases}$.
∴直线BC对应的函数表达式为y=−3x+3.设点P的横坐标为t,则P(t,−t²−2t+3);设点E的横坐标为c,则E(c,−3c+3).
∴−3c+3=−t²−2t+3,解得c=$\frac{t²+2t}{3}$.
∴E($\frac{t²+2t}{3}$,−t²−2t+3).
∴PE=$\frac{t²+2t}{3}$−t=$\frac{t²−t}{3}$.
∴S△PBC=$\frac{1}{2}$×$\frac{t²−t}{3}$×3=3,解得t₁=−2,t₂=3.
∴点P的纵坐标为−(−2)²−2×(−2)+3=3或−3²−2×3+3=−12.
∴点P的坐标为(−2,3)或(3,−12).

(1)把A(−3,0),B(1,0)代入y=ax²+bx+3,得$\begin{cases}9a - 3b + 3 = 0 \\ a + b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1 \\ b = -2\end{cases}$.
∴抛物线对应的函数表达式为y=−x²−2x+3.
(2)存在.
∵A(−3,0),B(1,0),
∴AB=4.在y=−x²−2x+3中,令x=0,则y=3,
∴C(0,3).
∴OC=3.
∴S△ABC=$\frac{1}{2}$AB·OC=$\frac{1}{2}$×4×3=6.
∴S△PBC=$\frac{1}{2}$S△ABC=3.如图,过点P作PE//x轴,交BC于点E,连结BP,CP.设直线BC对应的函数表达式为y=mx+n.将B(1,0),C(0,3)代入,得$\begin{cases}m + n = 0 \\ n = 3\end{cases}$,解得$\begin{cases}m = -3 \\ n = 3\end{cases}$.
∴直线BC对应的函数表达式为y=−3x+3.设点P的横坐标为t,则P(t,−t²−2t+3);设点E的横坐标为c,则E(c,−3c+3).
∴−3c+3=−t²−2t+3,解得c=$\frac{t²+2t}{3}$.
∴E($\frac{t²+2t}{3}$,−t²−2t+3).
∴PE=$\frac{t²+2t}{3}$−t=$\frac{t²−t}{3}$.
∴S△PBC=$\frac{1}{2}$×$\frac{t²−t}{3}$×3=3,解得t₁=−2,t₂=3.
∴点P的纵坐标为−(−2)²−2×(−2)+3=3或−3²−2×3+3=−12.
∴点P的坐标为(−2,3)或(3,−12).

8. 如图,在平面直角坐标系中,抛物线$y= ax^{2}+bx+c与x轴交于点A(3,0)$,$B(-1,0)$,与$y轴交于点C$,且$OC= 3OB$,顶点为$D$,连结$OD$,交$AC于点E$.
(1)求抛物线对应的函数表达式;
(2)$P为抛物线的AD$部分上一动点,过点$P作PF // DE交AC于点F$,探究四边形$DPAF面积的最大值及此时点P$的坐标.
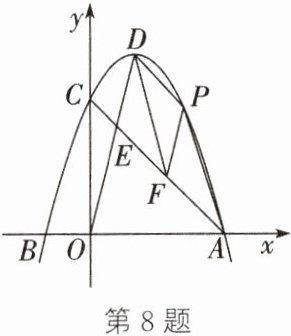
(1)求抛物线对应的函数表达式;
(2)$P为抛物线的AD$部分上一动点,过点$P作PF // DE交AC于点F$,探究四边形$DPAF面积的最大值及此时点P$的坐标.

答案:
(1)
∵A(3,0),B(−1,0),
∴OA=3,OB=1.
∵OC=3OB,
∴OC=3.
∴C(0,3).将A(3,0),B(−1,0),C(0,3)代入y=ax²+bx+c,得$\begin{cases}9a + 3b + c = 0 \\ a - b + c = 0 \\ c = 3\end{cases}$,解得$\begin{cases}a = -1 \\ b = 2 \\ c = 3\end{cases}$.
∴抛物线对应的函数表达式为y=−x²+2x+3.
(2)
∵y=−x²+2x+3=−(x−1)²+4,
∴D(1,4).如图,过点E作EM⊥OA于点M,过点P作PN⊥OA于点N,连结EP.
∵DE//PF,
∴S△DPF=S△EPF.
∴S四边形DPAF=S△APF+S△DPF=S△APF+S△EPF=S△APE.设P(m,−m²+2m+3),1<m<3,则ON=m,PN=−m²+2m+3.设直线AC对应的函数表达式为y=kx+n,把A(3,0),C(0,3)代入,得$\begin{cases}n = 3 \\ 3k + n = 0\end{cases}$,解得$\begin{cases}k = -1 \\ n = 3\end{cases}$.
∴直线AC对应的函数表达式为y=−x+3①.设直线OD对应的函数表达式为y=dx,将D(1,4)代入,得d=4.
∴直线OD对应的函数表达式为y=4x②.联立①②,得$\begin{cases}y = 4x \\ y = -x + 3\end{cases}$,解得$\begin{cases}x = \frac{3}{5} \\ y = \frac{12}{5}\end{cases}$.
∴E($\frac{3}{5}$,$\frac{12}{5}$).
∴OM=$\frac{3}{5}$,ME=$\frac{12}{5}$.
∴MN=m−$\frac{3}{5}$.
∵NA=3−m,
∴S△APE=S四边形EMNP+S△ANP−S△AME=$\frac{1}{2}$(PN+EM)×MN+$\frac{1}{2}$AN·PN−$\frac{1}{2}$AM·ME=$\frac{1}{2}$(−m²+2m+3+$\frac{12}{5}$)×(m−$\frac{3}{5}$)+$\frac{1}{2}$(3−m)×(−m²+2m+3)−$\frac{1}{2}$(3−$\frac{3}{5}$)×$\frac{12}{5}$=−$\frac{6}{5}$m²+$\frac{18}{5}$m=−$\frac{6}{5}$(m−$\frac{3}{2}$)²+$\frac{27}{10}$.
∵−$\frac{6}{5}$<0,
∴当m=$\frac{3}{2}$时,S△APE取最大值,为$\frac{27}{10}$.
∴四边形DPAF面积的最大值为$\frac{27}{10}$,此时点P的坐标为($\frac{3}{2}$,$\frac{15}{4}$).

(1)
∵A(3,0),B(−1,0),
∴OA=3,OB=1.
∵OC=3OB,
∴OC=3.
∴C(0,3).将A(3,0),B(−1,0),C(0,3)代入y=ax²+bx+c,得$\begin{cases}9a + 3b + c = 0 \\ a - b + c = 0 \\ c = 3\end{cases}$,解得$\begin{cases}a = -1 \\ b = 2 \\ c = 3\end{cases}$.
∴抛物线对应的函数表达式为y=−x²+2x+3.
(2)
∵y=−x²+2x+3=−(x−1)²+4,
∴D(1,4).如图,过点E作EM⊥OA于点M,过点P作PN⊥OA于点N,连结EP.
∵DE//PF,
∴S△DPF=S△EPF.
∴S四边形DPAF=S△APF+S△DPF=S△APF+S△EPF=S△APE.设P(m,−m²+2m+3),1<m<3,则ON=m,PN=−m²+2m+3.设直线AC对应的函数表达式为y=kx+n,把A(3,0),C(0,3)代入,得$\begin{cases}n = 3 \\ 3k + n = 0\end{cases}$,解得$\begin{cases}k = -1 \\ n = 3\end{cases}$.
∴直线AC对应的函数表达式为y=−x+3①.设直线OD对应的函数表达式为y=dx,将D(1,4)代入,得d=4.
∴直线OD对应的函数表达式为y=4x②.联立①②,得$\begin{cases}y = 4x \\ y = -x + 3\end{cases}$,解得$\begin{cases}x = \frac{3}{5} \\ y = \frac{12}{5}\end{cases}$.
∴E($\frac{3}{5}$,$\frac{12}{5}$).
∴OM=$\frac{3}{5}$,ME=$\frac{12}{5}$.
∴MN=m−$\frac{3}{5}$.
∵NA=3−m,
∴S△APE=S四边形EMNP+S△ANP−S△AME=$\frac{1}{2}$(PN+EM)×MN+$\frac{1}{2}$AN·PN−$\frac{1}{2}$AM·ME=$\frac{1}{2}$(−m²+2m+3+$\frac{12}{5}$)×(m−$\frac{3}{5}$)+$\frac{1}{2}$(3−m)×(−m²+2m+3)−$\frac{1}{2}$(3−$\frac{3}{5}$)×$\frac{12}{5}$=−$\frac{6}{5}$m²+$\frac{18}{5}$m=−$\frac{6}{5}$(m−$\frac{3}{2}$)²+$\frac{27}{10}$.
∵−$\frac{6}{5}$<0,
∴当m=$\frac{3}{2}$时,S△APE取最大值,为$\frac{27}{10}$.
∴四边形DPAF面积的最大值为$\frac{27}{10}$,此时点P的坐标为($\frac{3}{2}$,$\frac{15}{4}$).

查看更多完整答案,请扫码查看


