第60页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
8.(2024·连云港)如图所示的网格中各个小正方形的边长均为1,涂色部分的图形分别记做甲、乙、丙、丁.其中,是相似形的为(
A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁
D
)A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁
答案:
D
9.如图,把一张矩形纸片对折两次后得到四个小矩形,如果每个小矩形都与原矩形相似,那么原矩形纸片的长与宽之比为(

A.$\sqrt{2}:1$
B.2:1
C.3:1
D.4:1
B
)
A.$\sqrt{2}:1$
B.2:1
C.3:1
D.4:1
答案:
B
10.如图,△ABC与△DEF位似,点O是它们的位似中心,且位似比为$\frac{1}{2}$,则△ABC与△DEF的周长之比为(
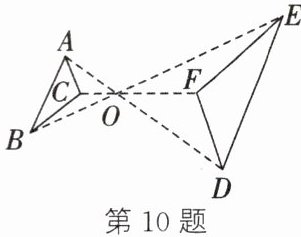
A.1:2
B.1:4
C.1:3
D.1:9
A
)
A.1:2
B.1:4
C.1:3
D.1:9
答案:
A
11.如图,D,E,F,G四点分别在△ABC的三边上,其中DG与EF相交于点H.若∠ABC= ∠EFC= 70°,∠ACB= 60°,∠DGB= 40°,则下列三角形相似的是(
A.△BDG和△CEF
B.△ABC和△EFC
C.△ABC和△BDG
D.△FGH和△ABC
B
)A.△BDG和△CEF
B.△ABC和△EFC
C.△ABC和△BDG
D.△FGH和△ABC
答案:
B
12.在每个小正方形的边长都为1的网格图中,每个小正方形的顶点称为格点,顶点都在格点上的三角形称为格点三角形.如图,Rt△ABC是6×6的网格图中的格点三角形,则该网格图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是______
5√2
.
答案:
5√2
13.如图,在△ABC中,D,E分别是边AB,BC上的点,且DE//AC.若$S_{\triangle BDE}:S_{\triangle CDE}= 1:4$,则$S_{\triangle BDE}:S_{\triangle ACD}=$
1:20
.
答案:
1:20
14.如图,点D在△ABC的边BC上.设点E,F分别为△ABD和△ADC的重心,连结EF.如果BC= 12,那么EF的长为
4
.
答案:
4
15.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木.问:出南门几何步而见木?”这段话摘自《九章算术》,大意如下:如图,矩形城邑ABCD的东边城墙AB长9里,南边城墙AD长7里,东门E,南门F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG= 15里,HG经过点A,则FH的长为
1.05
里.
答案:
1.05
查看更多完整答案,请扫码查看


