《2025年通城学典课时作业本九年级数学全一册浙教版》

8. 如图,点O为$\overset{\frown}{ACB}$所在圆的圆心,∠AOC= 108°,点D在AB的延长线上,且BD= BC,连结CD,则∠D的度数为 (A)
A.27°
B.30°
C.33°
D.54°

答案： A

9. (2023·株洲)如图,A,B,C是⊙O上不同的三点,点O在△ABC内,连结BO,CO,延长BO交AC于点D.若∠A= 60°,∠OCD= 40°,则∠ODC的度数为$80^\circ$.

答案： $80^\circ$ 解析:
∵ $\angle A = 60^\circ$,
∴ $\angle BOC = 120^\circ$.
∴ $\angle DOC = \angle BOC = 120^\circ$.
∴ $\angle ODC = 180^\circ - \angle OCD - \angle DOC = 180^\circ - \angle OCD - \angle BOC = 180^\circ - 40^\circ - 60^\circ = \angle ODC = 180^\circ - \angle OCD - \angle DOC = \angle ODC = \angle ODC = 80^\circ$.

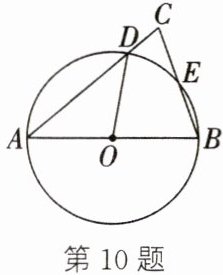
10. (2024·舟山定海段考)如图,在△ABC中,AB= AC,以AB为直径的⊙O分别交AC,BC于点D,E,连结OD.
(1)求证:E是BC的中点；
(2)若∠C= 70°,求∠BOD的度数.

答案：

10.
(1) 如图,连结 AE. $\because$ AB 是$\odot O$的直径,$\therefore$ AE $\perp$ BC.

$\because$ AB = AC,$\therefore$ E 是 BC 的中点.

(2) $\because$ AB = AC,$\therefore$ $\angle$ B = $\angle$ C = $70^{\circ}$.

$\therefore$ $\angle$ BAC = $180^{\circ}$ - $\angle$ B - $\angle$ C = $40^{\circ}$.

$\because$ $\angle$ BAC = $\frac{1}{2}$ $\angle$ BOD,$\therefore$ $\angle$ BOD = $80^{\circ}$.

11. (转换法)如图,在由边长为1的小正方形组成的正方形网格中,A,B,O均是格点,OA为⊙O的半径,P是$\overset{\frown}{AMB}$的中点,连结AP,BP,AB.
(1)∠APB=45°；
(2)求△APB的面积.
如图, 过点 B 作 $BC \perp PA$ 于点 C, 则 $\angle PCB = 90^\circ$.
∵ P 是$\widehat{AMB}$的中点,
∴ $\widehat{PA} = \widehat{PB}$.
∴ $PA = PB$. 由（1）, 知 $\angle APB = 45^\circ$,
∴ $\angle PBC = 90^\circ - 45^\circ - 45^\circ$.
∴ $PC = BC$.
∴ $\triangle PBC$ 是等腰直角三角形. 设 $PC = BC = x$, 则易知 $PA = PB = \sqrt{2}x$.
∴ $AC = PA - PC = (\sqrt{2} - 1)x$.
∵ $AB^2 = AC^2 + BC^2$, $AB = \sqrt{AO^2 + BO^2} = \sqrt{2}$,
∴ $2 = [(\sqrt{2} - 1)x]^2 + x^2$.
∴ $x^2 = \frac{2 + \sqrt{2}}{2}$.
∴ $S_{\triangle APB} = \frac{1}{2}PA \cdot BC = \frac{\sqrt{2}}{2}x^2 = \frac{\sqrt{2} + 1}{2}$

答案： （1）45 （2）如图, 过点 B 作 $BC \perp PA$ 于点 C, 则 $\angle PCB = 90^\circ$.
∵ P 是$\widehat{AMB}$的中点,
∴ $\widehat{PA} = \widehat{PB}$.
∴ $PA = PB$. 由（1）, 知 $\angle APB = 45^\circ$,
∴ $\angle PBC = 90^\circ - 45^\circ - 45^\circ$.
∴ $PC = BC$.
∴ $\triangle PBC$ 是等腰直角三角形. 设 $PC = BC = x$, 则易知 $PA = PB = \sqrt{2}x$.
∴ $AC = PA - PC = (\sqrt{2} - 1)x$.
∵ $AB^2 = AC^2 + BC^2$, $AB = \sqrt{AO^2 + BO^2} = \sqrt{2}$,
∴ $2 = [(\sqrt{2} - 1)x]^2 + x^2$.
∴ $x^2 = \frac{2 + \sqrt{2}}{2}$.
∴ $S_{\triangle APB} = \frac{1}{2}PA \cdot BC = \frac{\sqrt{2}}{2}x^2 = \frac{\sqrt{2} + 1}{2}$