第49页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
7. 如图,在等边三角形 ABC 中,点 D,E 分别在 AC,AB 上,且$\frac{AD}{AC}= \frac{1}{3}$,AE= BE,则下列结论正确的是(
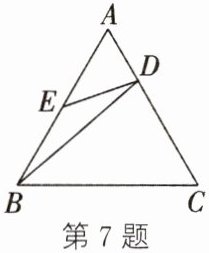
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
B
)
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
答案:
B
8. 如图,在△ABC 中,D 为边 BC 上一点,$BC= \sqrt{3}AB= 3BD$,则 AD∶AC 的值为______
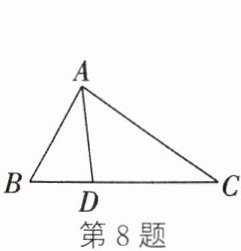
$\frac{\sqrt{3}}{3}$
.
答案:
$\frac{\sqrt{3}}{3}$
9. (分类讨论思想)(2024·绍兴上虞期中)如图,在△ABC 中,AB= 10 cm,BC= 20 cm,点 P 从点 A 出发,沿 AB 以 2 cm/s 的速度运动到点 B 停止,同时点 Q 从点 B 出发,沿 BC 以 4 cm/s 的速度运动到点 C 停止,则经过
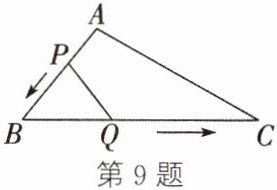
1或2.5
s,△PBQ 与△ABC 相似.
答案:
1或2.5 解析:设经过t s后,△PBQ与△ABC相似,则有AP=2t cm,BQ=4t cm,BP=(10-2t)cm. ① 当△PBQ∽△ABC时,有$\frac{PB}{AB}=\frac{BQ}{BC}$,即$\frac{10-2t}{10}=\frac{4t}{20}$,解得t=2.5. ② 当△QBP∽△ABC时,有$\frac{QB}{AB}=\frac{BP}{BC}$,即$\frac{4t}{10}=\frac{10-2t}{20}$,解得t=1.
∴经过2.5s或1s,△PBQ与△ABC相似.
∴经过2.5s或1s,△PBQ与△ABC相似.
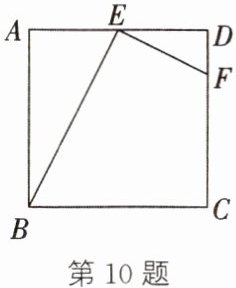
10. 如图,在正方形 ABCD 中,E 是边 AD 的中点,点 F 在边 CD 上,且 CF= 3FD,连结 BE,EF,则△ABE 与△DEF 相似吗? 请说明理由.

答案:
△ABE∽△DEF 理由:设正方形ABCD的边长为a,则AB=AD=DC=a.
∵E是边AD的中点,CF=3FD,
∴AE=DE=$\frac{1}{2}a$,DF=$\frac{1}{4}a$.
∵$\frac{AB}{DE}=\frac{a}{\frac{1}{2}a}=2$,$\frac{AE}{DF}=\frac{\frac{1}{2}a}{\frac{1}{4}a}=2$,
∴$\frac{AB}{DE}=\frac{AE}{DF}$. 又
∵在正方形ABCD中,∠A=∠D=90°,
∴△ABE∽△DEF.
∵E是边AD的中点,CF=3FD,
∴AE=DE=$\frac{1}{2}a$,DF=$\frac{1}{4}a$.
∵$\frac{AB}{DE}=\frac{a}{\frac{1}{2}a}=2$,$\frac{AE}{DF}=\frac{\frac{1}{2}a}{\frac{1}{4}a}=2$,
∴$\frac{AB}{DE}=\frac{AE}{DF}$. 又
∵在正方形ABCD中,∠A=∠D=90°,
∴△ABE∽△DEF.
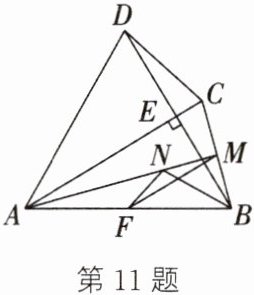
11. 如图,在四边形 ABCD 中,F,M 分别是 AB,BC 的中点,AC⊥BD 于点 E,BN 平分∠ABE,交 AM 于点 N,AB= AC= BD,连结 MF,NF.
(1) 判断△BMN 的形状,并证明你的结论;
(2) 判断△MFN 与△BDC 之间的关系,并说明理由.
(1) 判断△BMN 的形状,并证明你的结论;
(2) 判断△MFN 与△BDC 之间的关系,并说明理由.

答案:
(1)△BMN是等腰直角三角形
∵AB=AC,M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∴∠BMN=90°,∠BAN=$\frac{1}{2}∠BAC$.
∵AC⊥BD,
∴∠AEB=90°.
∴∠BAE+∠ABE=90°.
∵BN平分∠ABE,
∴∠ABN=$\frac{1}{2}∠ABE$.
∴∠MNB=∠BAN+∠ABN=$\frac{1}{2}(∠BAE+∠ABE)=\frac{1}{2}×90°=45°$. 又
∵∠BMN=90°,
∴∠MBN=∠MNB=45°.
∴MB=MN.
∴△BMN是等腰直角三角形 (2)△MFN∽△BDC 理由:
∵F,M分别是AB,BC的中点,
∴MF是△ABC的中位线.
∴MF//AC,且MF=$\frac{1}{2}AC$. 又
∵AC=BD,
∴MF=$\frac{1}{2}BD$. 即$\frac{MF}{BD}=\frac{1}{2}$. 由(1),得△BMN是等腰直角三角形,MN=BM. 又
∵M是BC的中点,
∴MN=BM=$\frac{1}{2}BC$.
∴$\frac{MN}{BC}=\frac{1}{2}$.
∴$\frac{MF}{BD}=\frac{MN}{BC}$.
∵∠BMN=90°,
∴∠NMF+∠BMF=90°. 设BD与FM相交于点H.
∵MF//AC,
∴∠FHB=∠AEB=90°.
∴∠CBD+∠BMF=90°.
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
∵AB=AC,M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∴∠BMN=90°,∠BAN=$\frac{1}{2}∠BAC$.
∵AC⊥BD,
∴∠AEB=90°.
∴∠BAE+∠ABE=90°.
∵BN平分∠ABE,
∴∠ABN=$\frac{1}{2}∠ABE$.
∴∠MNB=∠BAN+∠ABN=$\frac{1}{2}(∠BAE+∠ABE)=\frac{1}{2}×90°=45°$. 又
∵∠BMN=90°,
∴∠MBN=∠MNB=45°.
∴MB=MN.
∴△BMN是等腰直角三角形 (2)△MFN∽△BDC 理由:
∵F,M分别是AB,BC的中点,
∴MF是△ABC的中位线.
∴MF//AC,且MF=$\frac{1}{2}AC$. 又
∵AC=BD,
∴MF=$\frac{1}{2}BD$. 即$\frac{MF}{BD}=\frac{1}{2}$. 由(1),得△BMN是等腰直角三角形,MN=BM. 又
∵M是BC的中点,
∴MN=BM=$\frac{1}{2}BC$.
∴$\frac{MN}{BC}=\frac{1}{2}$.
∴$\frac{MF}{BD}=\frac{MN}{BC}$.
∵∠BMN=90°,
∴∠NMF+∠BMF=90°. 设BD与FM相交于点H.
∵MF//AC,
∴∠FHB=∠AEB=90°.
∴∠CBD+∠BMF=90°.
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
查看更多完整答案,请扫码查看


